by Tanya Khovanova, Konstantin Knop, Alexey Radul and Peter Sarnak
Let n coins weighing 1, 2, … n be given. Baron Münchhausen knows which coin weighs how much, but his audience does not. Define a(n) to be the minimum number of weighings the Baron must conduct on a balance scale, so as to unequivocally demonstrate the weight of at least one of the coins.
In the paper Baron Münchhausen’s Sequence, three of us completely described the Baron’s sequence. In particular, we proved that a(n) ≤ 2. Here we would like to outline another proof idea, which is interesting in part because it touches the Riemann hypothesis.We denote the total weight of coins in some set A as |A|.
Lemma. Numbers n that can be represented as Ti + Tj + Tk = 3n, where i ≤ j < k, such that there is a subset A of coins from j + 1 to k such that n = Tj + |A|, can be done in two weighings.
Proof. Suppose Ti + Tj + Tk = 3n and there is a subset A of coins from j + 1 to k such that n = Tj + |A|. We propose the two weighings
[1…j] + A = n
and
[1…i] + B = n + A,
where B is the complement of A in {j + 1, j + 2, … , k}.
If we sum up twice the first weighing with the second weighing we get
3[1…i] + 2[(i + 1)…j] + 2A + B = 3n + A.
In other words, three times the weight of the coins that were on the left side in both weighings, plus twice the weight of the coins that were on the left side in only the first weighing, plus the weight of the coins that were moved from the left cup to the right cup plus the weight of the coins on the left cup in only the second weighing equals three times the weight of the coin on the right cup in both weighings. Hence three times the weight of the coin on the right cup in both weighings can’t be less than the weight of the k other coins that participated plus the weight of the j coins that were on the left cup in the first weighing and weren’t moved to the right cup, plus the weight of the i coins that were one the left cup in both the first and the second weighing. But because Ti + Tj + Tk = 3n, then 3n is the smallest possible weight of any set of i plus j plus k coins, the coin on the right cup in both weighings has to be the n-coin.
We checked that any number up to 600,000 except 20 can be represented so as to satisfy the Lemma. To show how to solve 20 coins in two weighings is easy, and, as usual, is left as an exercise for the reader. Next, we want to look at the following lemma.
Lemma. Given a set of consecutive numbers {(j + 1), … , k}, if k > 2j + 2, then it is possible to find a subset in the set that sums up to any number in the range from j + 1 to (j + k + 1)(k – j)/2 – j – 1.
We won’t prove the lemma, but it means that if k is about twice larger than j, then we have a lot of flexibility for building our set A in the weighing above. For moderately large n (where 600000 >> “moderately large”), it is not hard to prove that this flexibility is sufficient.
Now the question becomes: can we find such a decomposition into triangular numbers? It is enough to find a representation Ti + Tj + Tk = 3n, where Tk is at least 81% of 3n.
We know that decompositions into triangular numbers are associated with decompositions into squares. Namely, if Ti + Tj + Tk = 3n, then (2i + 1)2 + (2j + 1)2 + (2k + 1)2 = 24n + 3. If the largest square is at least 81% of 24n + 3, then the largest triangular number in the decomposition of 3n is at least 81%.
There is a theorem (W. Duke, Hyperbolic distribution problems and half-integral weight Maass forms, in Inventiones Math 92 (1988) p.73-90) that states that in the limit the decompositions of numbers into three squares are equidistributed. That is, if we take some region on the unit sphere x2 + y2 + z2 = 1 (for example, the region |z| > 0.8) and view decompositions of 24n + 3 into squares as points on the sphere x2 + y2 + z2 = 24n + 3, then, as n grows, decompositions whose projections fall into our chosen region are guaranteed to appear.
This theorem is great, because it tells us that for large enough n we will always be able to find a decomposition of 24n + 3 into triangle numbers where one of the triangle numbers will be much bigger than the others, and it will be possible to prove the weight of the n coin in two weighings. Unfortunately, this summary, as stated, does not tell us how large that n needs to be. So we need some exact estimates.
The number of decompositions of m into sums of three squares is about the square root of m. More precisely, it is possible to compute a number N, such that for any number m > N, with at most one exception, the number of decompositions is at least Cm1/2−1/30, where C is a known constant.
The more specific statement of Duke’s theorem is that if the number of solutions to the quadratic x2 + y2 + z2 = 24n + 3 is large, for a computable value of “large”, then the solutions are equidistributed. More precisely, let us denote 3n by m and fix an area Ω on the unit sphere. Then the number of solutions (x, y, z) such that the unit vector (x, y, z)/|(x, y, z)| belongs to Ω is
1/(4π) Ωh(8m+3) + E(m),
where h(8m+3) is the total number of solutions of x2 + y2 + z2 = 24n + 3, and E(m) is an error term, which starting from some number satisfies the inequality: E(m) ≤ 1000m1/2-1/7.
That’s pretty good, because combining these two lets us, at least in principle, actually calculate an N such that for all n > N except maybe one a(n) = 2. After that we hoped to write a program to exhaustively search smaller numbers by computer.
This situation is still somewhat annoying, because that possible exception must then be propagated into the proof, and if we are not careful, possibly into the final theorem. (“No matter how many coins the Baron has, he can prove the weight of one in at most two weighings, except maybe one number of coins, and we don’t know which…”) This is where the Riemann Hypothesis comes in. If the Riemann Hypothesis is true, then that exception isn’t there, and all is sunlight and flowers.
The beauty of the Baron’s puzzle is such that we actually do not need the Riemann hypothesis. As we can use unbalanced weighings, it is enough to find a good decomposition for one out of the four numbers 3n, 3n-1, 3n-2, or 3n-3.
Instead of finding all these exact estimates we found a different elementary proof of our theorem. But we are excited that methods that are used in very advanced number theory can be used to solve a simple math problem that can be described to middle school children.
It would be great if someone decided to finish this proof.
Share:





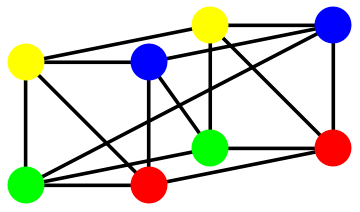 As soon as I realized that there is such a graph-theoretical object, I started to run around MIT asking everyone if such objects were studied or have a name.
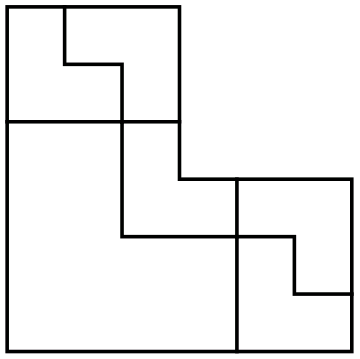
As soon as I realized that there is such a graph-theoretical object, I started to run around MIT asking everyone if such objects were studied or have a name.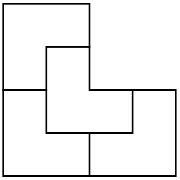 I remember a math problem from my childhood: divide an L-shaped triomino into four congruent parts. The answer is in the picture on the left. Such division is quite appropriately called a reptile (repetitive tiling).
I remember a math problem from my childhood: divide an L-shaped triomino into four congruent parts. The answer is in the picture on the left. Such division is quite appropriately called a reptile (repetitive tiling). 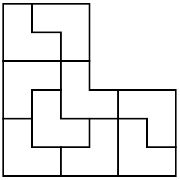

 Only at MIT. Room 4-231.
Only at MIT. Room 4-231. I am used to thinking that a “woman in numbers” means a female number theorist. But not anymore. I just discovered drawings by
I am used to thinking that a “woman in numbers” means a female number theorist. But not anymore. I just discovered drawings by 

