Tanya Khovanova's Math Blog

Vouchers are supposed to make shopping cheaper, right? Apparently, the shopkeeper in the following puzzle didn’t know. By the way, the puzzle is from Mathematical Puzzles and Curiosities, my book with Ivo David and Yogev Shpilman.

Puzzle. A shop sells vouchers with price tags of 1, 2, 3, … dollars. There is exactly one voucher of each price. Buying the voucher tagged N makes your very next voucher cost N times its own price tag. Each multiplier applies only to the next purchase; the multipliers do not accumulate. Your first voucher costs exactly its price tag.

You have 26 dollars. What is the largest number of vouchers you can buy?

For example, buying the vouchers tagged 1, 2, 3, and 4, in that order, costs 1 + 1 · 2 + 2 · 3 + 3 · 4 = 21 dollars.

I will leave the 26-dollar puzzle to you. Meanwhile, suppose you have already chosen a finite set of vouchers and must buy all of them. In what order should you buy them to spend as little as possible? And what order makes you spend as much as possible?

My PRIMES STEP students and I chose this puzzle as the starting point in our research. We got many results and wrote a paper From a Voucher Puzzle to Extremal Sums of Adjacent Products, available on arXiv.

Here is the coolest part: the cheapest and the most expensive purchase orders depend only on the ranks of the price tags. They work for any finite set of distinct positive integers. You need to know which price is smallest, second-smallest, and so on. You do not need to know what the actual prices are.

Let us play with four vouchers. For price tags 1, 2, 3, and 4, the cheapest orders are 3, 2, 1, 4 and 2, 3, 1, 4 for the total cost of 15 dollars. The most expensive orders are 2, 4, 3, 1 and 3, 4, 2, 1 for the total cost of 25 dollars.

Now suppose the shop changes the price tags to 2, 7, 10, and 100. These numbers are much less evenly spaced. It looks as though we should start over with new calculations. We do not have to. We simply replace the smallest old number by the smallest new number, the second-smallest by the second-smallest, and so on. The first cheapest order becomes 10, 7, 2, 100 for the total cost of 10 + 70 + 14 + 200 = 294 dollars, and the first most expensive order becomes 7, 100, 10, 2 for the total cost of 7 + 700 + 1000 + 20 = 1,727 dollars.

We also studied two relatives of the voucher cost. The pairwise cost is what you pay if the first voucher is free but still applies its multiplier to the next purchase: just add the products of neighboring price tags. For the order 1, 2, 3, 4, this gives 1 · 2 + 2 · 3 + 3 · 4 = 20 dollars. For the loop cost, arrange the price tags in a circle and include the product of the last and first tags too, giving 20 + 4 · 1 = 24 dollars. Both variations have recipes for minimizing and maximizing the cost: and again the result depends only on the ranks of the price tags.

In all three costs, we have the same intuition. To maximize the cost, we want to cluster the most expensive vouchers together, creating large products of neighboring price tags. For the smallest cost, we want to put the largest price tags next to the smallest ones.

There is a particularly tidy order maximizing all three costs. Number the vouchers by rank, starting with 1 for the cheapest. Take the even ranks in increasing order, followed by the odd ranks in decreasing order. For eight vouchers, this gives 2, 4, 6, 8, 7, 5, 3, 1. These are ranks, not prices: all eight actual price tags could be odd. The minimizing orders also use only ranks, although they weave the large and small numbers together differently.

For more examples, and the exact results, check our paper From a Voucher Puzzle to Extremal Sums of Adjacent Products.

Let me begin with labeled chip-firing on an infinite directed binary tree, where the root is at the top. Place 2ⁿ chips, labeled from 0 to 2ⁿ − 1, at the root. A move consists of choosing any two chips at the same vertex and firing them: the smaller chip goes to the left child, and the larger chip goes to the right child. For k ≥ 2, the k-ary version is exactly what you would guess. Start with kⁿ chips, labeled from 0 to kⁿ − 1, at the root. When a vertex fires, choose k chips and send them, from smallest to largest, to its k children from left to right.

The process eventually stops. At that point, there is exactly one chip at every vertex n edges below the root. If we erase the labels, the final configuration is always the same. With the labels, however, our choices matter. Reading the chips on the final layer from left to right gives a permutation of the numbers from 0 to kⁿ − 1.

Let us play with eight chips, labeled 0 through 7, on a binary tree. Here is one particularly orderly strategy. At the root, fire the pairs

(0, 4),   (1, 5),   (2, 6),   (3, 7).

The left child receives chips 0, 1, 2, and 3, while the right child receives chips 4, 5, 6, and 7. Continue in the same spirit. At every vertex, pair the smaller half of its chips with the larger half, in order. Each vertex then sends its smaller half to the left and its larger half to the right. In the final configuration, the chips appear as

0, 1, 2, 3, 4, 5, 6, 7.

This is, of course, the lexicographically earliest possible permutation. It is difficult to beat being completely sorted.

What about the lexicographically latest possible permutation? This time, at every vertex, list the chips in increasing order and pair neighboring entries. At the root, we fire

(0, 1),   (2, 3),   (4, 5),   (6, 7).

Thus, the left child receives the even-numbered chips, while the right child receives the odd-numbered chips. We continue in the same way. The left child fires the pairs (0, 2) and (4, 6), while the right child fires the pairs (1, 3) and (5, 7). Continuing to the last layer gives the permutation

0, 4, 2, 6, 1, 5, 3, 7.

For eight chips, this is the lexicographically latest attainable final configuration.

Here is the cool part. Write the labels in binary. Our final permutation becomes

000,   100,   010,   110,   001,   101,   011,   111.

Now reverse the bits in every string. We get

000,   001,   010,   011,   100,   101,   110,   111.

Aha! These are simply the numbers in their usual order.

This permutation has the rather grand name of a radix-2 digit-reversal permutation. In base 2, it is usually called a bit-reversal permutation.

The binary notation also explains the firing strategy. First, we write our numbers as binary strings of length 3. At the root, we paired numbers whose binary representations differed only in the last digit. On the next layer, we paired numbers that differed only in the middle digit. On the last firing layer, we paired numbers that differed only in the first digit. Counting the binary digits from left to right, this strategy examines them in the order 3, 2, 1.

Our first strategy has an equally simple description. At the root, we paired numbers that differed in the first binary digit. On the next layer, they differed in the second digit, and on the last firing layer, they differed in the third. Thus, the first strategy corresponds to the permutation 123, while the second corresponds to 321.

Once this trick is visible, a whole family of firing strategies appears when we start with 2ⁿ chips. Choose any permutation w = w₁w₂…w_n of the digit positions 1, 2, …, n. At stage i, at each vertex on the current layer, pair chips whose binary strings agree everywhere except in position w_i. In other words, chips with a 0 in that position go left, and chips with a 1 go right.

For example, the strategy corresponding to permutation 132 first separates the chips according to their first binary digit, then according to their third digit, and finally according to their second digit. Starting with eight chips, this strategy produces the final permutation

0, 2, 1, 3, 4, 6, 5, 7.

Everything works in exactly the same way on a k-ary tree, mutatis mutandis—with things changed that should be changed.

There are now two different kinds of permutations hiding in the same game. The strategy permutation has length n and tells us the order in which to examine the digit positions when firing. The final permutation has length kⁿ and describes the order of the chips on the last layer. How are these two permutations related?

• The first observation is that the firing strategy corresponding to the identity permutation produces the lexicographically earliest final configuration, in which the labels appear in increasing order.
• At the other extreme, the firing strategy corresponding to the reverse of the identity permutation produces the radix-k digit-reversal permutation. Theorem 3.3 of our paper (link below) shows that this is the lexicographically latest configuration among permutation-based strategies. In fact, although we did not state this stronger result in the paper, a short induction shows something stronger: the digit-reversal permutation is lexicographically latest among all attainable final configurations.
• Two different strategy permutations always produce two different final configurations.

There is also a more subtle relation between the two permutations. It is not quite true that a lexicographically earlier strategy permutation always produces a lexicographically earlier final permutation. There is a small twist. Given a strategy permutation w, reverse it and then replace every entry i by n + 1 − i. Call the resulting permutation B(w). We proved that the final configuration corresponding to w is lexicographically earlier than the one corresponding to w′ exactly when B(w) is lexicographically earlier than B(w′).

We also counted inversions and descents in the resulting permutations, as one naturally does when permutations unexpectedly emerge from a chip-firing game. These results about permutation-based strategies, and more, appear in our paper Permutation-based Strategies for Labeled Chip-Firing on k-ary Trees, written jointly with Ryota Inagaki and Austin Luo. The paper was published in Discrete Mathematics & Theoretical Computer Science, volume 28:2 (2026), and is also available on arXiv.

In a recent post, Each Point has Three Closest Neighbors, I mentioned the following conjecture.

Karabegov’s Conjecture. Any finite planar point configuration in which every point has exactly 3 closest neighbors must contain at least 16 points.

The conjecture was proposed by my dear friend Alexander Karabegov, whom I met in 1974. Wait. What?! I just realized that this was more than 50 years ago. How is that even possible?

After I posted the conjecture, we couldn’t resist working on it. We wandered through different types of graphs and found many cute definitions related to our problem.

A unit distance graph is formed from points in the plane by connecting two points whenever they are exactly distance 1 apart. A matchstick graph is a unit distance graph that can be drawn in the plane with edges of length 1 that do not cross. In other words, it is a unit distance graph that behaves nicely, by being planar. Think of laying matchsticks flat on a table: no overlaps, no chaos.

Here’s the difference visually: the left graph is a unit distance graph, while the right one is a matchstick graph.

Now for the star of the story. A penny graph connects two vertices if and only if their distance is the minimum distance among all pairs of vertices. The name is delightfully literal: imagine placing identical pennies at each vertex so that they do not overlap. Two pennies touch exactly when the corresponding vertices are connected by an edge. A penny graph is a special kind of matchstick graph: two vertices that are not connected are at a distance that is longer than the length of the matchstick.

Finally, a 3-regular graph is a graph where every vertex has degree 3. Three neighbors. No more, no less. They are also called cubic graphs. Not surprisingly, if the vertices of a cube are the vertices of our graph, and the edges of a cube are the edges of our graph, we get a 3-regular graph, as each vertex is incident to exactly 3 edges. Surprisingly, such graphs are not called tetrahedron graphs, as a tetrahedron, too, has each vertex incident to 3 edges. But the tetrahedron graph is special: it is a minimal 3-regular graph.

We wrote a paper Minimal 3-regular Penny Graph, in which we proved the conjecture. The conjecture has officially graduated to a theorem.

Theorem. The minimal 3-regular penny graph has 16 vertices.

I recently gave my STEP students a question from our old 2014 PRIMES entrance test.

Puzzle. John’s secret number is between 1 and 2¹⁶ inclusive, and you can ask him yes-or-no questions, but he may lie in response to one of the questions. Explain how to determine his number in 21 questions.

Here is the standard solution. We start by asking John to convert his number into binary and add zeros at the beginning if needed to make the result a binary string of length 16. For the first 15 questions, we do the following. For question i, we ask: “Is the i-th digit of your string zero?” For question 16, we ask, “Have you lied in response to a previous question?” If he lied on a previous question, he must say YES. If he didn’t, he might lie on question 16 and also say YES. In any case, if the answer is NO, he didn’t lie on the first 15 questions and we know the first 15 digits of the number. Then, we ask about the last digit three times, and the answer given at least twice is correct, so we know the number.

If the answer to question 16 is YES, then he lied on one of the questions 1–16. From now on, he has to tell the truth since he already lied. We use binary search (4 questions) to determine on which question he lied. This will tell us the first 15 digits, and we can use the 21st question to find the last digit.

One of my students, Tanish, invented an out-of-the-box solution that uses 18 questions. The idea is to force John to lie in the first two questions, and then safely proceed with the binary search.

He suggested asking the following two questions: “Are you going to answer NO in response to the next question?” and “Did you respond YES to the previous question?” The reader can check that whatever John replies, he is forced to lie exactly once.

Another student, Vivek, had a similar idea but used only one question to force John to lie: “Will you say NO to this question?”

Imagine you’re watching a magician. She pulls out two perfectly ordinary boxes — or so it seems. One box is inside the other, like a set of nesting dolls. So far, nothing suspicious.

Then she removes the smaller box, closes the larger one, and slides the larger box inside the smaller one. Ta-da!

The name comes from the way one box goes into the other. Would you like to know the secret? The two boxes are actually identical. Moreover, they are not cubes but cuboids. The inner box is fully closed, while the outerbox is slightly expanded, and the inner box is rotated relative to the outer one.

I first heard about Gozinta Boxes at the Gathering for Gardner conference in 2024. Ivo David gave a talk and presented his new trick: Triple Gozinta Boxes, which you can now buy at TCC Magic. He can place three boxes inside one another — and then repeat the trick in the reverse order.

During his presentation, David mentioned that he knew how to prove that you cannot have more than ten Gozinta Boxes. My immediate reaction was that ten must be overkill. So I decided to give the problem to my STEP students as a project.

We proved that in three or higher dimensions, the maximum number of boxes is three. We also showed that in two dimensions, the maximum is four. You can find all the details in our paper Mathematics of Gozinta Boxes, posted on the arXiv. But we didn’t stop there. We invented a new trick. We constructed three boxes such that not only can they be nested in one order — say, ABC — and in the reverse order, CBA, but they can also be nested in three additional orders, for example ACB, BAC, and BCA. We also proved that achieving all six possible orders is impossible. You can see the trick by following the link for A New Gozinta Boxes Trick.

I met Alexander Karabegov during the All-Soviet Math Olympiad in Yerevan. He was one year older than me. By then, when I was still competing in 1976, he was already a freshman at Moscow State University. He proposed the following two related puzzles for the Moscow Olympiad, which I had to solve.

Puzzle 1. You are given a finite number of points on a plane. Prove that there exists a point with not more than 3 closest neighbors.

Just in case, by closest neighbors I mean all points at the minimal distance from a given point. I am sure I solved both puzzles at the time. I leave the solution to the first one to the reader.

Puzzle 2. Can you place a finite number of points on the plane in such a way that each point has exactly 3 closest neighbors?

The last problem has an elegant solution with 24 points chosen from a triangular grid. The story continued almost 40 years later, when Alexander sent me an image (below) of such a configuration with 16 points. He conjectures that this is the minimal configuration.

Karabegov’s Conjecture. Any finite planar point configuration in which every point has exactly 3 closest neighbors must contain at least 16 points.

Can you prove it?

Initially, I didn’t want to give the 24-points solution, but the image above is a big hint, so here you go.

Both constructions reveal the same underlying pattern. The constructions consist of rhombuses formed by two equilateral triangles, and the rhombuses are connected to each other. The 24-point construction consists of 6 rhombuses, while the 16-point construction consists of 4 rhombuses. What will happen if we try the construction with 3 rhombuses? The image below shows such a configuration, which now has extra edges with the shortest distance. We now see 3 points with more than three closest neighbors each, violating the condition. So the conjecture doesn’t break.

So far, every smaller attempt failed — can you prove that 16 is minimal?

Once I wrote a blog essay titled Seven, Ace, Queen, Two, Eight, Three, Jack, Four, Nine, Five, King, Six, Ten. It was about a “magic” card trick. Magic trick. Take a deck of cards face down. Move the top card to the bottom, then deal the new top card face-up on the table. Repeat this process until all the cards are dealt. And — abracadabra — the cards come out in perfect order!

If you want to perform this trick with one suit, the title of that earlier post tells you exactly how to stack your deck.

In the fall of 2023, I gave this trick as a homework problem to my STEP students. The result? We ended up writing a 40-page paper, Card Dealing Math, now available on the arXiv. At one point, we seriously considered calling it The Art of the Deal, but decided against it.

In the homework version, the deck consisted of cards from a single suit, but we generalized it to a deck of N cards labeled 1 through N. The dealing process we studied is called under–down dealing: you alternate between placing one card under the deck and then dealing the next one face-up. It’s very similar to down–under dealing, where you start by dealing the first card instead. These two patterns are often, unsurprisingly, called the Australian dealings.

The under-down dealing turns out to be mathematically equivalent to the Josephus problem. In that famous ancient problem, people are arranged in a circle, and you repeatedly skip one person and execute the next (much grimmer than playing with cards). The classic question asks: given N people, who survives? In our card context, this corresponds to asking where the card labeled N ends up in the prepared deck.

More generally, the Josephus problem can ask the following question. If we number the people in a circle 1 through N, in what order are they eliminated? In our research, we flipped the question around: how should we number the people in the circle so that they’re eliminated in increasing order?

Naturally, we couldn’t stop there. We explored several other dealing patterns, discovered delightful mathematical properties, and along the way added 44 new sequences to the OEIS. The funnest part? We also invented a few brand-new card tricks.

We recently wrote a blog post on how to generalize the game of SET and promised to continue. Here we are. But first, a reminder of what the game of SET is.

In the game of SET, we have 81 cards, each containing one, two, or three of the same object. The object is green, red, or purple, the shape is squiggly, oval, or diamond, and the shading is empty, full, or stripped. Three cards form a set if, for every feature, the attributes are all the same or all different. An example of a set with all features different is shown below. By the way, such sets are usually more difficult to spot. In the game, you need to find sets as fast as you can.

If we assign each attribute value a number 0, 1, or 2, we get an equivalent definition of a set. Three cards form a set if and only if the values for each feature sum to zero modulo 3. Thus, we can see our cards as vectors in the space F₃⁴. Three vectors form a set if they sum up to 0.

The generalizations we described in the previous post, were the following. We pick a different group and define a set as a few cards that might need to be in a specific order that multiply to the group’s identity.

However, there is a different way to generalize sets to groups. Three cards that form a set in a classical game of SET, taken in any order, form an arithmetic progression. In other words, if a, b, and c form a set, then vectors b−a and c−b are the same. We can check this. We have c−b = c−(c+b+a)−b =−2b−a = b−a.

Thus, we can generalize the game of SET differently. Suppose cards are vectors in some space. We say three of them, a, b, and c, form a set if and only if b−a = c−b. Now, the order becomes important, similar to our previous generalization. We do not need to use commutative groups like vector spaces. For any group, our condition is equivalent to ba^-1 = cb^-1. Thus, c = ba^-1b.

Interestingly, we do not care much about the identity card, meaning the card deck is a torsor. We introduced the notion of a torsor before, which informally is a group that forgets about its identity. Now, let’s check possible examples.

Suppose the values of one attribute correspond to Z₄. This game is not very inspiring as two values, a=0 and b=2, can be completed to a set with the third card, which equals c=(0,0,0) and is already used. The next interesting example is Z₅. Here, values a=0 and b=2 can be completed to a third value c=4. We will leave it to the reader to check that for any two cards, a and b, the third card, c, differs from both a and b.

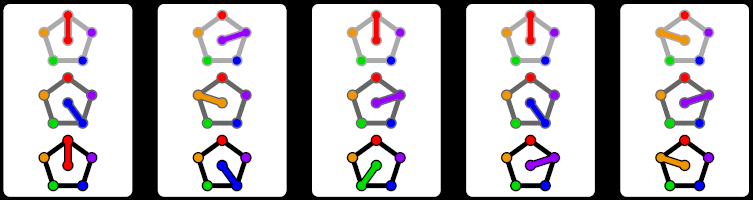
To make it more visual, we can use a pentagon with one marked direction. We fix the pentagon in space. In this case, three cards form a set if and only if the directions of the first and the third card are symmetric with respect to the direction of the second card. If we want to use three pentagons, we can reuse the cards from the game C53T, we described in our previous post. To make this game more visual, we can use three pentagons. We can mark each coordinate with a direction on the corresponding pentagon. The colors are to allow players to visually process the cards faster. For theoretical purposes, the colors can be ignored. Also, the pentagons themselves have different intensities of gray to emphasize that the game is played on each of them separately and also help choose the top of the card.

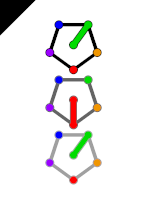
Let us go back and calculate when it is possible that the element that completes a set is already used. If our initial elements are a and b, then we need ba^-1b to complete a set. If this element is equal to b, then a = b, which contradicts the assumption that we start with two different cards. Suppose ba^-1b = a, then, equivalently (ba^-1)² = 1. The new element can be the one that is already used if and only if the group contains elements of order 2.

Can we use other decks we described in the previous post? Consider the game ProSet/Socks. The group is commutative, and every element is of order 2, which means ba^-1b is always a. We can’t use the deck at all! What about the EvenQuads deck? It can be viewed as Z₄³, so it is possible that we can’t complete any two cards to a set. However, there is a bigger problem with the deck. To play with it, we need to actually assign values to colors and shapes. We are saying that even if we decide to use the group, we should make different cards! For example, we can style the cards as squares like the pentagons above.

We also mentioned in the previous post the group, which is the wreath product of S₂ and S₃. Consider the following example of two cards that were screen-printed from the Numberphile video on the variations of the game of SET.

The first card, a, is the inverse of itself, so the third card we are looking for is described as the product bab, which we can visualize as the following. If we ignore the beads, the card that completes the set is a. Luckily, if we do not ignore the beads, it is not a; we need to add two beads to a.

The product of permutations is difficult to visualize, so playing this game with the cards in the Numberphile video might be difficult. The good news is that this group can be visualized in many different ways:

• The group of symmetries of a cube, meaning its rotations and reflections;
• The group of symmetries of an octahedron, meaning its rotations and reflection;
• The wreath product of S₂ and S₃;
• The direct product of S₄ and S₂.

We want to show you a beautiful deck from the tsetse website that allows you to use any one of the four definitions to play the game. The game is called OCTA Set, as the underlying group is called an octahedral group. An example of a set is in the image below, where the top and bottom shapes represent the same element of the group. Moreover, the deck is a torsor: there is no the identity card.

• The top shape represents an octahedron where the opposite faces are the same color. Thus, the top shape shows a unique rotation of an octahedron. All the swirls are the same in the image, but in other cards, the swirl could be white. Two different swirls mean that the octahedron needs to be reflected to get from one shape to the other. In our example above, no reflection is involved, so all the swirls are black.
• We can ignore that the top shape represents an octahedron and only look at the choice of colors. The changes of colors represent a permutation in S₄ and a swirl represents an element in S₂.
• The bottom shape represents a cube where the opposite faces are the same color. One of the faces is solid, and the opposite face is hollow. This way, one can reconstruct the complete shape of a cube by the top three faces.
• We can ignore that the top shape represents a cube and only look at the choice of colors. The colors form a permutation, and the beads correspond to changing the hollowness of a color. When viewing the cube this way, the permutation acting on the colors is S₃, and each color has its hollowness associated with an element of S₂. This exactly corresponds to the wreath product of S₃ and S₂.

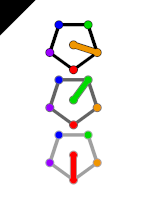
Let us prove that this is a set. Consider the bottom cube shape. Comparing the first two cards, the top face doesn’t change. We can see that the symmetry of the cube is the 90-degree clockwise rotation around the line that goes through the centers of green faces. In such a rotation, the left face on the second card keeps the color from the first card, while the right face takes the color from the left face on the first card and swaps hollowness. We see that the third cube completes the set.

For another proof, let us look at the top shape and discuss what happens with the permutation of colors when changing from the first card to the second. The left color moves to the bottom, the bottom color to the right, the right color to the center, and the center color to the left. Not surprisingly, we got a cyclic permutation of order 4, similar to a 90-degree rotation being of order 4. The same thing happens when moving from the left to the right. The swirl stays the same.

As we mentioned, when you play this game and pick two cards then calculate what card completes the set, you might discover that it is one of the cards you picked. The probability that two cards in a specific order can’t be completed into a set is the same as the probability of picking a random element in our group and discovering that it has order 2. The symmetric group S₄ has 9 elements of order 2. Thus, the direct product with S₂ has 19 elements of order 2, giving a probability of 19/48. For completeness, this group also has 8 elements of order 3, 12 elements of order 4, 8 elements of order 6, not to mention the identity of order 1.

If ba^-1 is an element of order three, then the cards a, b, and the card c that completes the set form a set when they are taken in any order. As a tradition in mathematical writing, we leave it to the reader to check that fact. Just a reminder that in the game of SET, the group element ba^-1 always has order 3.

Notably, there was nothing special or extraordinary about the group discussed above. It has a pretty visualization as a cube or octahedron, but is not otherwise particularly interesting. The reason why this group allowed for these two platonic solids to be used to visualize it is because the cube is dual to the octahedron. But we could have similarly used any group to play set! One such example might consider using the group of symmetries of the other pair of dual platonic solids, the icosahedron and the dodecahedron. This group is actually equivalent to A₅, also known as the alternating group of order 5, which consists of all even permutations of five elements. The tsetse website we mentioned above contains an implementation of such a game called A5SET (pronounced “asset”). The design of the site, games, and cards was done by Andrew Tockman and Della Hendrickson.

The world is full of groups and symmetries. Any group can be turned into a game of SET!

Foams are cool mathematical objects studied by my brother, Mikhail Khovanov. I already wrote about them in my previous blog posts, Foams Made out of Felt and Tesseracts and Foams. Here, I would like to explain why foams are so cool, but first, I need to remind you of their definition. Foams are finite 2-dimensional CW-complexes, such that each point’s neighborhood must be homeomorphic to one of the three objects below.

• An open disc. Such points are called regular points.
• The product of a tripod and an open interval. Such points are called seam points.
• The cone over the 1-skeleton of a tetrahedron. Such points are called singular vertices.

Foams are cool: they are 2-dimensional CW-complexes embedded in 3-space, with singularities only of the most generic kind, which makes them relatively simple. Moreover, they are combinatorially defined, which makes them easier to work with than with many other geometric objects.

My two previous blog posts have some pictures, but now, I just want to discuss a generic planar cross-section of a foam, which is a planar graph. In the cross-section, seams become vertices, and faces (regular points) become edges. The tripod condition above implies that the resulting graph is trivalent: each vertex has degree 3.

The most interesting foams are tricolarble: foams where their faces can be colored in three colors, so that each face has its own color, and, at the seams, three faces of three different colors meet. The cross-section of such a foam makes a tricolorable trivalent graph. This coloring is called Tait coloring. The cool thing is the Tait’s theorem connects the Tait coloring to the 4-color theorem.

Tait’s theorem. The following two statements are equivalent.

• Every planar graph is 4-colorable.
• The edges of every planar bridgeless trivalent graph are 3-colorable.

I won’t discuss the proof here, but I will explain how to color the edges of a graph in three colors when the faces are colored in four, and vice versa.

Assume that the four colors of the faces form a group of four elements, called the Klein group. Let’s say that gray is the identity, and red, blue, and green are the rest. Then, the product of gray and x is x. The product of any two non-gray colors is the third non-gray color.

Given a trivalent graph G whose edges are colored in three colors, we can color the faces of that graph in the following manner. Color one of the faces a random color. Then, calculate the colors of the other faces so that each edge’s color is the product of the colors of neighboring faces.

Going back, if we have a planar trivalent graph with faces colored in four colors, we can assign an edge a color that is the product of the colors of neighboring faces. As neighboring faces have different colors, the product of those colors is never gray (the identity). Thus, the edges will be colored in three colors. I leave it to the reader to check that three edges incident to a vertex must be colored in different colors.

Kronheimer-Mrowka homology theory of graphs states that the Kronheimer-Mrowka homology of a trivalent graph is non-zero if and only if the graph has no bridge. If one can prove that the rank of the homology group is the number of 3-colorings of the edges (or at least that the non-zero homology implies the existence of the tricoloring of that graph), then the Four-color theorem would follow from Tait’s theorem.

Foams are cool by themselves, but there is hope that they might provide a conceptual proof of the Four-color theorem, making them awesome!

Do you know that 2025 is a composite, deficient, evil, odd, square, and powerful number? I collect properties of numbers at my Number Gossip website, where you can also find detailed definitions of these terms. Provocatively, 2025 is also an apocalyptic power, meaning that 2 to the power of 2025 contains 666 as a substring.

Recently, Tamas Fleischer sent me an email discussing additional fascinating properties of 2025. While I am slowly deciding whether to add them to my database, there is some urgency in posting these properties in anticipation of the coming year. Here’s the material from Tamas, retold in my own words.

Out of the properties mentioned earlier, the square property is the only rare one. On my website, I define a property as rare if fewer than 100 numbers below 10,000 possess it. Square numbers barely make the cut. But 2025 is not just a square number—it is the square of a triangular number. If you remember the formula for the sum of cubes of the first n natural numbers, the result is (n(n+1)/2)^{2, which is the square of the nth triangular number. Thus, 2025 is the sum of the cubes of all one-digit numbers.}

Additionally, 2025 is the product of 25 and 81. My website notes an intriguing property shared by 25 and 2025: both remain square numbers when all their digits are incremented by 1. For example, 25 becomes 36, and 2025 becomes 3136, both of which are squares. Moreover, 25 is the smallest such number, and 2025 is the second smallest. What my website does not mention is that their square roots exhibit a similar pattern. The square roots of 25 and 2025 are 5 and 45, respectively. When their digits are incremented by 1, the results are 6 and 56, the square roots of 36 and 3136, respectively. The original and incremented squares and their square roots are tied together in a surprising way.

2025 also shares an interesting property with 81. Both are square numbers with an even number of digits and if you split the digits in half and sum the halves, the result is the square root of the original number. For 81, splitting into 8 and 1 gives 8 + 1 = 9, which is the square root of 81. Similarly, for 2025, splitting into 20 and 25 gives 20 + 25 = 45, the square root of 2025. Intriguingly, 81 is the smallest number with this property, and 2025 is the second smallest.

Thank you, Tamas, and Happy New 2025 to everyone!