Tanya Khovanova's Math Blog

Once, I gave a puzzle to my students as homework just to check their level of attention.

Puzzle. A family has two identical twins. One of them is a boy, what is the probability that the other one is a boy?

What can I say? Some of the students didn’t pay attention and gave weird answers like 1/2, 1/3, and 2/3.

The twins are IDENTICAL. The other one has to be a boy! Duh!

One of the students was well-educated and mentioned that it is theoretically possible for different twins to be different genders, though this is extremely rare. When one fertilized egg splits into two, producing two embryos, the genetic material of both eggs is the same, almost. Some errors during splitting are possible, and it seems that some very particular errors can lead to the identical twins being identified as a boy and a girl. I never knew that before!

However, one student thought outside the box. In his vision, a family adopted two identical twins who aren’t each other’s twins, just happen to be identical twins with someone else.

Here is a puzzle for middle school students from the Möbius tournament.

Puzzle. For which natural numbers n greater than 1 it is possible to arrange n numbers 1 through n in a circle so that the difference between two neighbors always divides n?

A new hat puzzle from Gribalko, reminding me of traffic lights.

Puzzle. You and six of your mathematician friends each have a hat placed on your head. Each of you can see the hats of all the others but cannot see your own. You were all told that there were three red, three yellow, and three green hats in total, but two of them were hidden. Your friends began to say the following phrases in sequence:

• First: “I don’t know what color my hat is.”
• Second: “I also don’t know what color my hat is.”
• Third: “I also don’t know what color my hat is.”
• Fourth: “I know that my hat is red.”
• Fifth: “But I still don’t know what color my hat is.”
• Sixth: “And I am sure that my hat is yellow.”

Can you determine what color hat you have on your head?

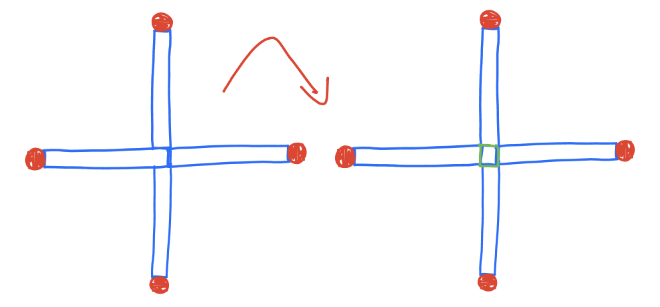
I once saw a TikTok video featuring a puzzle: four matches were arranged to form a plus sign, and the challenge was to move one match to create a square. The solution shown differed from what first came to my mind, so I decided to share the puzzle with my students. Instead of drawing a diagram, I described it to them in words.

Puzzle. Arrange four matches to form a plus sign. Move one match to form a square.

Most of my students gave the same solution shown in the video: moving one match slightly away from the center to create a square in the center, with the inner edges of the matches forming its borders. Not all the students were as lazy as I was; some drew pictures to illustrate. One example is shown below, where the resulting square is in green.

My solution, also discovered by a couple of students, was to move one match to form the number 4, which is a square.

I am glad I didn’t provide a picture because it led to two unexpected solutions. For the first one, imagine a 3D shape out of four matches where one projection forms three sides of a square, and the other one is a plus sign. We can take the match from the plus sign that is not a side of a square and use it to complete the square. The second solution is shown below. The arrangement already contains a small square, so you can take a match and put it back. Being lazy brings benefits!

Here is another riddle I discovered in a book and gave as homework to my students.

Puzzle. I can use the number 20 thrice to make 60: 20 + 20 + 20 = 60. Make it 60 again by using a different number three times.

The book’s answer was to use 5: 55 + 5 = 60.

My students were very inventive. All of them solved the puzzle, but only one out of ten students came up with the book’s answer.

• For most of them, the new number was 60, as in 60 + 60−60 = 60, or 60*60/60.
• Some used −60 or 1/60, as in −60 − (−60) − (−60) = 60, or ((1/60)/(1/60))/(1/60) = 60. Similarly, some multiplied the cube root of 60 three times.
• One student used 59 in a clever way, as in 59 + 59/59 = 60.
• Another student said the following. If you turn 60 upside-down, you will make 09, and now you can use the number 3 thrice: 3+3+3 = 09.
• And the last on my list is the student who said that 42 has to be the answer to the universe and everything. He summed up two instances of 42 to get 84 and then subtracted the third instance of 42 with the digits flipped to get 84 − 24 = 60.

When I was in 8th grade, I was selected to be part of the Moscow math team and went to Yerevan, Armenia, to participate in the All-Soviet Math Olympiad. A group of us boarded a bus, and Alexander Karabegov paid for all of our bus tickets. He was from Yerevan himself and wanted to be a gracious host. I was impressed. The next time I met him was when I started studying at the Moscow State University. We have been friends ever since. He was even the best man at one of my weddings. Now, he lives in Texas and sends me his original puzzles from time to time. Today, he sent me a new one.

WARNING. His solution to the puzzle is also included. So if you want to solve it yourself, stop reading after the next paragraph.

Puzzle. A number c is called a fixed point of a function f, if it is a solution of the equation f(x) = x; that is, if f(c) = c. Find all solutions of the equation g(g(x)) = x, where g(x) = x² + 2x − 1; that is, find all fixed points of the function f(x) = g(g(x)). (We can assume that x is a real number.)

I gave the puzzle to my students, and they converted it to a fourth-order equation, which they solved using various methods. What I liked about Alexander’s solution is it only uses quadratic equations. I am too lazy to give his full solution. Here is just his solve path.

Solve path. If c is a fixed point of the function g(x), then it is a fixed point of f(x) = g(g(x)). Solving the equation g(c) = c gives us two fixed points. We need two more, as our equation is quartic. Suppose a is another fixed point. Let b = g(a). It follows that g(b) = a. Moreover, we can assume that a is not b, as we covered this case before. We get two equations a² + 2a − 1 = b and b² + 2b − 1 = a. Subtracting one equation from another, we get a quadratic equation that has to be divisible by a −b. As b is not a, by our assumption, we can divide the result by a − b, expressing b as a linear function of a. We plug this back into one of the two equations and get a quadratic equation for a, supplying us with the remaining two solutions. TADA!

Here’s one by Sergei Luchinin, designed for 7th graders.

Puzzle. We have an 8-by-8 chessboard, but it’s not colored in the usual checkerboard pattern. Instead, all cells in odd-numbered columns are black, and all cells in even-numbered columns are white. A limping rook is placed in the lower-left corner and can only move one cell to the right or one cell up. The rook’s goal is to reach the upper-right corner.
The question is: Are there more paths that pass through more white cells, or more that pass through more black cells?

Here is a new report of interesting homework solutions from my students.

Puzzle. One day, two sisters decided to clean the old shed at the bottom of their garden. When they finished cleaning, one had a dirty face and the other had a clean face. The sister with the clean face went and washed her face, but the girl with the dirty face did not wash. Why should this be so?

The expected answer: The sister with the clean face saw her sister’s dirty face and assumed her own face must be dirty as well, so she washed it. The sister with the dirty face saw her sister’s clean face and assumed her own face must also be clean, so she didn’t feel the need to wash.

Another student suggested a different but quite realistic answer.

The realistic answer: The sisters’ home ran out of water after the clean sister washed her face, preventing the dirty sister from washing her own.

The other student watched too many sitcoms.

The sitcom answer: The sister with the dirty face purposefully kept her face dirty, so she could show her parents that she did all the work, as she was the only one with dirt on her face.

I asked ChatGPT to solve the puzzle, and, unsurprisingly, it came up with the standard answer. I pushed and got the following.

The ChatGPT answer: The sister with the clean face washed up because she was an Instagram influencer and couldn’t risk being seen dirty, even in her own garden. Meanwhile, the sister with the dirty face was a carefree adventurer who believed dirt was “nature’s makeup.” Plus, she figured that if she waited long enough, the dirt would either blow away or blend into a trendy new skincare routine—”Exfoliation by Shed Dust.”

Here’s a fresh challenge from the recent Tournament of the Towns, crafted by Alexander Shapovalov.

Puzzle. A mother and her son are playing a game involving cheese and butter. The son starts by cutting a 300-gram block of cheese into 4 pieces. Then, the mother divides 280 grams of butter between two plates. Afterward, the son places the cheese pieces onto these same plates. The son wins if, on both plates, there is at least as much cheese as butter. If not, the mother wins. Can either the mother or the son guarantee a win, regardless of the other’s moves?

I love hat puzzles, and this one, posted on Facebook by Konstantin Knop, is no exception.

Puzzle. The sultan decided to test his three sages once again. This time, he showed them five hats: three red and two green. Each sage was blindfolded and had one hat placed on their head. When the sages removed their blindfolds, they could see the hats on the other sages but not their own. The twist in this puzzle is that one of the sages is color-blind and cannot distinguish red from green. The sages are all friends and are aware of each other’s perception of color. The sages are then asked, in order, if they know the color of their hats. Here’s how the conversation unfolded:

• Alice: I do not know the color of my hat.
• Bob: Me too, I do not know the color of my hat.
• Carol: Me too, I do not know the color of my hat.
• Alice: I still do not know the color of my hat?

The question is: Who is color-blind?