Tanya Khovanova's Math Blog

The term fibonometry was coined by John Conway and Alex Ryba in their paper titled, you guessed it, “Fibonometry”. The term describes a freaky parallel between trigonometric formulas and formulas with Fibonacci (F_n) and Lucas (L_n) numbers. For example, the formula sin(2a) = 2sin(a)cos(a) is very similar to the formula F_2n = F_nL_n. The rule is simple: replace angles with indices, replace sin with F (Fibonacci) and cosine with L (Lucas), and adjust coefficients according to some other rule, which is not too complicated, but I am too lazy to reproduce it. For example, the Pythegorian identity sin²a + cos²a = 1 corresponds to the famous identity L_n² – 5F_n² = 4(-1)ⁿ.

My last year’s PRIMES STEP senior group, students in grades 7 to 9, decided to generalize fibonometry to general Lucas sequences for their research. When the paper was almost ready, we discovered that this generalization is known. Our paper was well-written, and we decided to rearrange it as an expository paper, Fibonometry and Beyond. We posted it at the arXiv and submitted it to a journal. I hope the journal likes it too.

The fine tenacious boys nicely joke to hated servant girls sick for (absent) king.

The picture shows John Conway’s notes in my journal. They are the mnemonic for setting up his trick. For example, the word “tenacious” sounds similar to “ten” and “ace”. Hence, we arrange 13 cards in this order: 3, 5, 10, A, J, 9, joker, 2, 8, 7, Q, 6, and 4. We also put the king aside. The trick looks better if the cards are the same suit.

The fun part of the trick is the story he told while showing it. Unfortunately, I do not remember the story. My only other note says:

One, two, three are done by me. Four, five, six: they do the tricks. Seven, eight, play them straight. We all try nine for quite a long time. The king is back.

Here is my attempt to recover the trick. We arrange the cards in the above order. We keep the cards face down so that the three is on top. Now, we spell the word “ACE”, and for each letter, we move one card from the top to the bottom of the pile. Then, we flip the next card from the top of the pile, and “tada”, the card is an ace. We put it aside. Now, we repeat the process by spelling “TWO”, and the next card after that is a two. We do the same for “THREE”.

But, when we try the same process for “FOUR”, we get the joker instead. This is not surprising if you remember that “Four, five, six: they do the tricks”. We put the joker at the bottom of the pile and continue. In the next round, after spelling “FOUR” again, we get 4, which we put aside. We proceed by spelling “FIVE” and getting a joker, then getting 5 after the second spelling. The same happens with “SIX”. Then we continue with “SEVEN” and “EIGHT” without getting the joker.

Then, we try “NINE”, and get the joker. Then, we spell it again and again and keep getting the joker. Clearly, we are in a cycle that can go on forever. If you recall the quote, “We all try nine for quite a long time.” To get out of this cycle, we remember our king and put it on top of the pile when the joker is on the bottom. We start again. And now we can spell “NINE” and get 9. We are back to normal with “TEN”, “JACK”, and “QUEEN”, too. The king, however, appears on the second try after spelling “KING”, getting the joker, and spelling “KING” again.

I do not remember the details of John’s performance. I tried to find the trick online but only saw it briefly mentioned in Mathematics, Magic, and Mischief with John H. Conway.

Have you seen this trick? Any juicy details are welcome in the comments.

Once, I was in Princeton and attended a lecture by Persi Diaconis. John Conway was also there. During his presentation, Persi mentioned John by referring to him as Wonderful John Conway. John couldn’t resist and said, “Thank you, you are one of not many people who remember my real first name.”

My favorite of the Escher plane tessellations is the one with shells. It is stunning, and the mathematics behind it is beautiful. I want to thank the late John Conway for teaching me the secret of this drawing.

Mathematicians are interested in tessellations because of the symmetries behind them. This tessellation has translational and rotational symmetries. Can you find them?

When I ask my students to find the rotational symmetries, they immediately tell me that they see two different 4-fold points, aka points where 90-degree rotations preserve the drawing. One point, I call G, is where four greenish shells meet, and one point, I call R, is where four reddish shells meet.

As you might have guessed, the students’ answer is not quite correct. There is more to the picture. Look at a dark-brown shell that looks like a curvy rectangle. This shape has markings. Now look at a specific point R and its four closest brown shells. You can see that going around this point R, the brown shells alternate their orientation: the darker side of these shells either faces towards point R or away.

The big secret of this artwork is that it contains TWO symmetry groups: a group and a subgroup. If we ignore the markings on the brown shells and consider them one solid color, then point R is indeed a 4-fold symmetry point. In addition, the center of the brown shape is a 2-fold symmetry point. Thus, the symmetry group of this simplified drawing is 442 in orbifold notation.

If we take the markings of the brown shells into account, then point R is not a 4-fold rotation, it is a 2-fold rotation. Point G keeps the property of being a 4-fold rotation. If you know your symmetry groups, you can conclude that there should be another 4-fold rotation. But where is it?

I will spill my answer. The symmetry point G is not ONE symmetry point anymore. There are two different points where greenish shells meet. The dark side of the brown shells faces one of them and looks away from the other.

The dark secret of this drawing is that it demonstrates two symmetry groups: group 442 and its subgroup 442, with different fundamental regions. To see the secret, you must look closely at a dark brown shell and find its darker side.

What is base 3/2? One of the ways to define such a base is to think of it in terms of exploding dots. What the heck are exploding dots? They are explained and popularized by James Tanton in his YouTube videos.

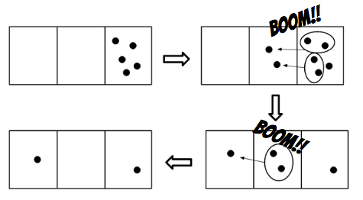
Essentially, “exploding dots” is a machine made of a row of boxes with rules describing how the dots loaded into the machine explode. As an example, let me describe the 1←2 machine, which corresponds to base 2. We load N dots into the rightmost box. Whenever there are 2 dots in one box, they explode into 1 dot in the box to the left.

For example, to write 5 in base 2, we would first load 5 dots in the rightmost box, as in the figure above. Then each group of 2 dots in the rightmost box would explode, and for each group, 1 dot would appear in the box to the left. Finally, the 2 dots in the second box would explode into 1 dot into the next box to the left. By reading the number of dots from left to right, we get 101, which is 5 in base 2.

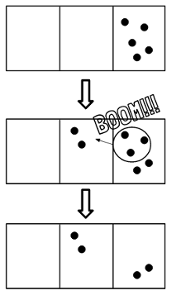
The interesting thing here is that there is no reason this model should be exclusive to integer bases. Suppose our rule is that 3 dots explode into 2 dots in the box to the left. Such a rule is called the 2←3 machine, and it corresponds to base 3/2. To represent 5 in this base, we load 5 dots into the rightmost box, then we use the exploding rule shown in the figure below. Using this machine, 5 is represented in base 3/2 as 22.

The figures were made by my junior PRIMES STEP group, in the 2017-2018 academic year, for our paper, Variants of Base 3 Over 2.

But, in this post, I want to discuss a different paper from the same academic year. With my senior PRIMES STEP group, we wrote a paper On Base 3/2 and its Sequences. A shorter version which includes a tribute to John Conway, appeared in The Mathematical Intelligencer.

Speaking of John Conway, he liked inventing new sequences, especially ones with unusual behaviors. One of his hobbies was tweaking the Fibonacci rule to create new sequences, which he called Fibs. For example, the sorted Fibs sequence starts the same as the Fibonacci sequence with 0 and 1. To calculate the next term, we add the two previous terms and sort the digits in non-decreasing order. In base 10, this sequence is A069638: 0, 1, 1, 2, 3, 5, 8, 13, 12, 25, 37, 26, …. It is known that this sequence is periodic with a maximum value of 667.

With my senior PRIMES STEP group, we studied analogs of this sequence in base 3/2. We begin with the sorted Fibs sequence f_n with the same two initial values that start the Fibonacci sequence: f₀ = 0 and f₁ = 1. To calculate f_n+1, we add f_n-1 and f_n in base 3/2 and sort the digits in non-decreasing order. It follows that the numbers in the sequence are written as several ones followed by several twos. Unlike base 10, the sequence is not periodic and grows indefinitely: 0, 1, 1, 2, 2, 12, 12, 112, 112, 1112, 1112, 11112, …. In recognition of the constant growth of this Fibs sequence, we call it the Pinocchio sequence.

Obviously, you can start the sorted Fibs sequence with any two numbers. But we proved an interesting theorem which stated that any sorted Fibs sequence eventually turns into either the tail of the Pinocchio sequence or the 3-cycle 112, 1122, 1122.

However, we didn’t stop there. There are two natural ways to sort the digits of a number, in increasing or decreasing order. Naturally, there is another type of sequences worth considering, in which the digits are sorted in non-increasing order. We called such sequences the reverse sorted Fibs.

We defined the reverse sorted Fibs sequence r_n in base 3/2 as follows. To calculate r_n+1, we add r_n-1 and r_n in base 3/2 and sort the digits in non-increasing order, ignoring zeros. It follows that after the initial terms, the terms of such a sequence are represented with several twos followed by several ones. We call the reverse sorted Fibs that start in a similar way to the Fibonacci sequence with r₀ = 0 and r₁ = 1, the proper reverse sorted Fibs. Here are several terms of the proper reverse sorted Fibs: 0, 1, 1, 2, 2, 21, 21, 221, 2211, 221, 221, 2211, 221, 221, 2211, …. This sequence becomes cyclic, starting from r₇.

We also found one reverse sorted Fibs growing indefinitely: 2211, 2211, 22211, 22211, 222211, 222211, and so on. We proved that any reverse sorted Fibs sequence eventually turns into either this sequence or a 3-cycle sequence: 221, 221, 2211. The similarity between the sorted Fibs and the reverse sorted Fibs surprised us. Up to the initial terms, they both have exactly one sequence which grows indefinitely and one 3-cycle. To emphasize this similarity, we reversed the word Pinocchio and named this growing reverse Fibs sequence the Oihcconip sequence.

Now I need to figure out how to pronounce the name of this new sequence.

One of my posts about John Conway has a picture I took of him in 2015, leafing through a book about himself, Genius at Play. I allowed Wikipedia to use this image, and they did. They also retouched it for their article on John Conway in Dutch. I like the result.

My friend, John Conway, had a trick to help him with tricky situations. Whenever he needed to make a non-trivial decision, he would ask himself, “What would John Conway do?” As he explained to me, he had in mind the public image he himself created. He liked the image and thought this mental trick helped him be a better, more productive, and not-to-forget, flashier person.

From time to time, I catch myself in need of a decision and ask myself, “What would John Conway do?” And he gave me the answer: I should change the question and ask myself, “What would Tanya Khovanova do?”

Yesterday I stumbled upon a picture of John Conway I completely forgot I had: it was saved in a wrong folder. The photo was taken at the MOVES conference in 2015. There is a third person in the original shot, but I do not remember her. I decided to cut her out as I didn’t know how to contact her for permission to post this photo.

(I wrote this piece for La Recherche. It was translated into French by Philippe PAJOT. You can find this piece and pieces by others at John Horton Conway: a magician of maths disappears.)

Unlike many other mathematicians I know, John Conway cared a lot about the way he presented things. For example, in the puzzle he invented—known as Conway’s Wizards—the wizards had to be riding on a bus. Why was the bus so important? You see, the numbers in the puzzle were related to the age of one of the wizards, the number of the bus, and the number of the wizard’s children. It was important to John that the readers be able to use a convenient notation a, b and c for these numbers and remember which number is which.

When I give my lecture on integers and sequences, I show my students a list of different famous sequences. The first question from the audience is almost always: “What are the Evil Numbers?” As you can guess the name for this sequence was invented by John Conway. This name was invented together with the name of another sequence which is called Odious Numbers. These two sequences are complementary in the same sense as even and odd numbers are complementary: every natural number is either evil or odious. The names are good, not only because they attract, but also because they help remember what the sequences are. Evil numbers are numbers with an even number of ones in their binary representation. I assume that you can interpolate what the odious numbers are.

When he was lecturing, John used all sorts of tricks to emphasize important points: From time to time I saw him shouting or throwing his shoes. Once I remember him staring at his statement written on the blackboard for a really long time. My neighbor in the lecture hall got uncomfortable. He assumed that John, who was at that time way over 70, was blanking out and had forgotten what he wanted to say. I calmed my neighbor down. It was my fourth time listening to the same lecture, including the same pause. John Conway didn’t forget.

The picture was taken on December 21 of 2019 at Parker Life care facility right before dinner.