Tanya Khovanova's Math Blog

In December 2022, I wrote a blog post Uncrossed Knight’s Tours about Derek Kisman’s amazing achievement of calculating the largest uncrossed knight’s tours on rectangular chessboards on sizes M-by-N, where M is small, and N can be very very large.

The data showed some asymptotic periodicity, and I wondered how to prove it mathematically. I didn’t realize that Derek already proved it. In my ignorance of programming, I assumed that programs just spewed out the data and didn’t think they could prove anything. I was wrong. It appears that no other proof is needed. Derek tried to explain the details to me using the terminology of dynamic programming, but I am not sure I can reproduce it here.

Let’s recall the problem. Consider an M-by-N chessboard and a knight that moves according to standard chess rules: jumping one square in one direction and two squares in an orthogonal direction. The knight must visit as many squares as possible, without repeats, and then return to its starting square. In addition, the knight may never cross its own path. If you imagine the knight’s path consisting of straight line segments connecting the centers of the squares it visits, these segments must form a simple polygon. To summarize, given M and N, we want to calculate the longest uncrossed knight’s tour length.

To be clear: the programs, their output data, proven answers, and images are by Derek Kisman. I am just a humble messenger showing my new appreciation of the power of a computational proof.

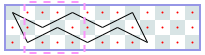
The image shows Derek’s solution for a 3-by-13 chessboard. There is a repeating 3-by-4 pattern marked by dashed lines. The same tour works for boards of lengths 10, 11, and 12. Thus, for chessboards of width 3 and length from 10 to 13 inclusive, the longest uncrossed knight’s tour is length 10. We can write the answers for 3-by-N chessboards as a sequence with index N, where -1 means the tour is impossible. The sequence starts with N = 1: -1, -1, -1, 4, 6, 6, 6, 6, 10, 10, 10, 10, 14, 14, ….

We can prove that this sequence is correct without programming. Suppose the tour starts in the leftmost column. If we start in the middle of the column, the whole tour ends as a rhombus and a tour of length 4, which, by the way, is the longest tour for N = 5. Thus, for a larger N, we have to start in a corner. From there, there are only two possible moves. We can see that the continuation is unique and that, asymptotically, we gain one step per extra column. That is, asymptotically, the length of the longest tour divided by N is 1.

Derek uses an additional notation in the following sequence: each cycle is in brackets. Any two consecutive cycles differ by the same constant. So to continue the sequence indefinitely, it is enough to know the first two cycles.

Closed tours: 3xN (asymptote 1):  -1, -1, -1, -1, 4, [6, 6, 6, 6], [10, 10, 10, 10], …

I continue with other examples Derek calculated:

Closed tours: 4xN (asymptote 2): -1, -1, -1, [4], [6], …

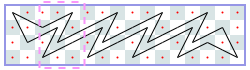
Closed tours: 5xN (asymptote 2 3/5):  -1, -1, 4, 6, [8, 12, 14, 18, 20, 22, 24, 28, 30, 34], [34, 38, 40, 44, 46, 48, 50, 54, 56, 60], …

Closed tours: 6xN (asymptote 4): -1, -1, 6, 8, 12, 12, 18, 22, 24, 28, 32, 36, [38], [42], …

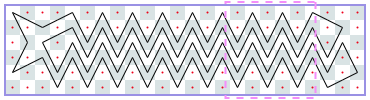
Closed tours: 7xN (asymptote 4 10/33):  -1, -1, 6, 10, 14, 18, 24, 26, 32, 36, 42, 44, 48, 54, 58, 62, 66, 72, 74, 80, 84, 88, 94, 98, 100, 106, 112, 114, 118, 124, 128, 130, [136, 140, 144, 148, 154, 158, 162, 166, 170, 176, 180, 184, 188, 192, 196, 200, 204, 210, 214, 218, 222, 226, 232, 236, 240, 244, 248, 254, 256, 260, 266, 270, 274], [278, 282, 286, 290, 296, 300, 304, 308, 312, 318, 322, 326, 330, 334, 338, 342, 346, 352, 356, 360, 364, 368, 374, 378, 382, 386, 390, 396, 398, 402, 408, 412, 416], …

Closed tours: 8xN (asymptote 6): -1, -1, 6, 12, 18, 22, 26, 32, 36, 42, 46, 52, 58, [64, 70, 76, 80, 88, 92], [100, 106, 112, 116, 124, 128], …

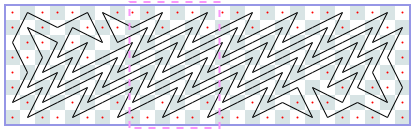
Closed tours: 9xN (asymptote 6 6/29): -1, -1, 6, 14, 20, 24, 32, 36, 42, 50, 56, 60, 68, 74, 80, 86, 94, 98, 106, 114, 118, 126, 132, 136, [144, 150, 156, 162, 168, 174, 180, 186, 192, 200, 206, 212, 218, 224, 230, 236, 242, 250, 254, 262, 268, 274, 280, 286, 292, 300, 304, 312, 318, 324, 330, 336, 342, 348, 354, 360, 366, 372, 378, 386, 392, 398, 404, 410, 416, 422, 428, 436, 440, 448, 454, 460, 466, 474, 478, 486, 492, 498], [504, 510, 516, 522, 528, 534, 540, 546, 552, 560, 566, 572, 578, 584, 590, 596, 602, 610, 614, 622, 628, 634, 640, 646, 652, 660, 664, 672, 678, 684, 690, 696, 702, 708, 714, 720, 726, 732, 738, 746, 752, 758, 764, 770, 776, 782, 788, 796, 800, 808, 814, 820, 826, 834, 838, 846, 852, 858], …

Closed tours: 10xN (asymptote 8): -1, -1, 10, 16, 22, 28, 36, 42, 50, 54, 64, 70, 78, 84, 92, 100, [106], [114], … I do not have an image for this case.

As you might have noticed, for an even M, the asymptote equals M-2. The asymptote for an odd M is slightly greater than the asymptote for M-1.

Derek also calculated the longest open knight’s tours: the tours where the knight doesn’t have to return to its starting position.

Open tours: 2xN (asymptote 1/2): -1, -1, [2, 2], [3, 3], …

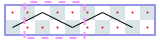
Open tours: 3xN (asymptote 1): -1, 2, 3, 5, 6, 7, [9], [10], …

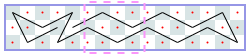
Open tours: 4xN (asymptote 2): -1, 2, 5, [6], [8], …

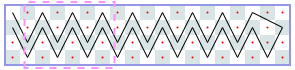
Open tours: 5xN (asymptote 3): -1, 3, 6, 8, 11, 15, 17, 20, 23, 26, 29, [32, 35, 38, 41, 44, 46], [50, 53, 56, 59, 62, 64], …

Open tours: 6xN (asymptote 4): -1, 3, 7, 10, 15, 18, 22, 26, 30, 33, [36], [40], …

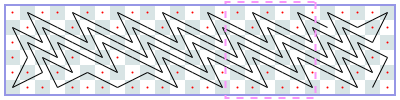
Open tours: 7xN (asymptote 5): -1, 4, 9, 12, 17, 22, 25, 31, 36, [40], [45], …

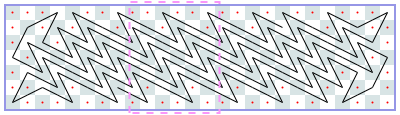
Open tours: 8xN (asymptote 6): -1, 4, 10, 14, 20, 26, 31, 36, 43, 48, 54, 60, [64], [70], …

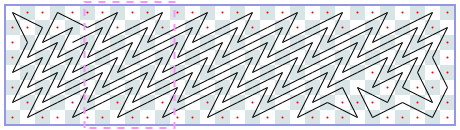
Open tours: 9xN open (asymptote 7): -1, 5, 11, 16, 23, 30, 36, 43, 48, 56, 62, 68, 75, [82, 88, 94], [103, 109, 115], … I do not have an image for this case.

There are a lot of interesting new sequences in this essay that were very nontrivial to calculate. I hope someone adds them to the OEIS database.

The 2018 International Collegiate Programming Contest (ICPC) had a very hard problem which is of interest to mathematicians. The problem was proposed by super-coder Derek Kisman. Here is the problem as it was presented at the contest.

Problem J. Uncrossed Knight’s Tour. A well-known puzzle is to “tour” all the squares of an 8 × 8 chessboard using a knight, which is a piece that can move only by jumping one square in one direction and two squares in an orthogonal direction. The knight must visit every square of the chessboard, without repeats, and then return to its starting square. There are many ways to do this, and the chessboard size is manageable, so it is a reasonable puzzle for a human to solve.

However, you have access to a computer, and some coding skills! So, we will give you a harder version of this problem on a rectangular m × n chessboard with an additional constraint: the knight may never cross its own path. If you imagine its path consisting of straight line segments connecting the centers of squares it jumps between, these segments must form a simple polygon; that is, no two segments intersect or touch, except that consecutive segments touch at their common end point. This constraint makes it impossible to visit every square, so instead you must maximize the number of squares the knight visits. We keep the constraint that the knight must return to its starting square. Figure J.1 shows an optimal solution for the first sample input, a 6 × 6 board.

The input consists of a single line containing two integers m (1 ≤ m ≤ 8) and n (1 ≤ n ≤ 10¹⁵), giving the dimensions of the rectangular chessboard.

Mathematicians know many things about knight tours on a standard 8 × 8 chessboard. But one of the limits in this puzzle is so huge, that the answer to this computational puzzle constitutes a new mathematical discovery. Unsurprisingly, no one solved this puzzle during the contest. A well-written solution summary is available on the ICPC website. The solution requires dynamic programming and a realization that tours have to have repeating patterns.

Since no one solved this problem during the competition, it is useful that, in addition to the solution summary, Derek posted his innovative code online. The two figures below (courtesy of Derek Kisman) show his answer for the longest closed tour on a 6 × 24 board and the longest open tour on a 6 × 26 board.

Derek got interested in uncrossed knight’s tours after reading my blog post, 2014 Math Festival in Moscow, where I presented the following problem given at that festival to 7th graders.

Problem. Inside a 5 × 8 rectangle, Bart draws closed paths that follow diagonals of 1 × 2 rectangles. Find the longest possible path.

The 2014 Math Festival organizers offered an extra point for every diagonal on top of 16. It is funny that the organizers obfuscated that it is useless to try and find 17 diagonals, as the number of diagonals has to be even. The official solution, shown below, had 24 diagonals.

In the solution booklet, the organizers mentioned that they did not know the best answer to their own question. They hoped that the longest possible path matched their official solution.

In Derek’s notation, the above problem is equivalent to finding the largest uncrossed knight’s closed tour on a 6 × 9 grid. And Derek proved that, indeed, 24 is the largest tour. While proving this, he also calculated the answer for gazillions of other boards.

We can go further: beyond gazillions. Let’s consider what happens on m × n boards, where m is fixed, and n is astronomically large. Suppose f_m(n) is the largest size of an uncrossed knight’s closed tour on the m × n board and g_m(n) is the largest size of an uncrossed open tour.

The answer has repeating patterns everywhere except around the ends of the board. We would expect that the number of possible repeating patterns is finite. Moreover, for large boards, only the densest patterns would appear. This means that asymptotically, both functions f and g are linear functions of n. On top of that, as each pattern is periodic, the behavior at the ends of the long boards should become periodic as well. Hence, the difference functions of f and g for fixed m would eventually become periodic. (Here, the f’s difference function, which I denote D(f_m) is defined as follows: D(f_m)(n) = f_m(n+1) – f_m(n).)

That means we can solve a more difficult problem. We do not need the limits for n. It should be possible to calculate these functions for a given m and any n (even if n is way more than a gazillion). I am being over-optimistic here. First, we need some mathematical theory to find the bounds for where the periodic behavior has to start and estimate the size of the period. Suppose we can prove that for D(f₆)(n), the eventual period has to start before n reaches A, and the length of the eventual period is not more than B. Then, we need to calculate the A + 2B values of the function f₆(n) to know the function for any n.

Derek actually calculated the functions f_m(n) and g_m(n) for m up to 9 and n up to infinity. More precisely, he found the cycles I am describing above. What a mindblowing achievement!

My son, Alexey Radul, is gainfully unemployed. While looking for a new job he wrote several essays about his programming ideas. I am a proud and happy mother. While I can’t understand his code, I understand his cutting-edge essays. Below are links to the four essays he has posted so far. He is also a superb writer. You do not need to take my word for it. Each link is accompanied by the beginning of the essay.

• Digital FoxesThe successful fox must know more than the sum of what the hedgehogs know, for it must know the connections from one thing to another. This fact is key to the design of computer systems for solving certain kinds of problems. Read more
• Introduction to Automatic DifferentiationAutomatic differentiation may be one of the best scientific computing techniques you’ve never heard of. If you work with computers and real numbers at the same time, I think you stand to benefit from at least a basic understanding of AD, which I hope this article will provide; Read more
• On the Cleverness of CompilersThe “Sufficiently Clever Compiler” has become something of a trope in the Lisp community: the mythical beast that promises language and interface designers near-unlimited freedom, and leaves their output in a performance lurch by its non-appearance. A few years ago, I was young enough to join a research project to build one of these things. Neglecting a raft of asterisks, footnotes, and caveats, we ended up making something whose essence is pretty impressive: you pay for abstraction boundaries in compile-time resources, but they end up free at runtime. One prototype was just open-sourced recently, so that makes now a good time to talk about it. Read more
• Cleverness of Compilers 2: HowThe Cleverness of Compilers essay described the name of the hyperaggressive compilation game in broad, philosophical strokes. Here, I would like to walk through the Mandelbrot example in some detail, so that the interested reader may see one particular way to actually accomplish that level of optimization. Read more

Share:

My new favorite hat puzzle was invented by Konstantin Knop and Alexander Shapovalov. It appeared (in a different wording) in March 2013 at the Tournament of the Towns:

A sultan decides to give 100 of his sages a test. The sages will stand in line, one behind the other, so that the last person in the line sees everyone else. The sultan has 101 hats, each of a different color, and the sages know all the colors. The sultan puts all but one of the hats on the sages. The sages can only see the colors of the hats on people in front of them. Then, in any order they want, each sage guesses the color of the hat on his own head. Each hears all previously made guesses, but other than that, the sages cannot speak. They are not allowed to repeat a color that was already announced. Each person who guesses his color wrong will get his head chopped off. The ones who guess correctly go free. The rules of the test are given to them one day before the test, at which point they have a chance to agree on a strategy that will minimize the number of people who die during this test. What should that strategy be?

I loved it so much that I wrote a paper about it. You can find the solution there.Share:

There is an array containing all the integers from 1 to n in some order, except that one integer is missing. Suggest an efficient algorithm for finding the missing number.

A friend gave me the problem above as I was driving him from the airport. He had just been at a job interview where they gave him two problems. This one can be solved in linear time and constant space.

But my friend was really excited by the next one:

There is an array containing all the integers from 1 to n in some order, except that one integer is missing and another is duplicated. Suggest an efficient algorithm for finding both numbers.

My friend found an algorithm that also works in linear time and constant space. However, the interviewer didn’t know that solution. The interviewer expected an algorithm that works in n log n time.

The company claims that they are looking for the smartest people in the world, and my friend had presented them with an impressive solution to the problem. Despite his excitement, I predicted that they would not hire him. Guess who was right?

I reacted like this because of my own story. Many years ago I was interviewing for a company that also wanted the smartest people in the world. At the interview, the guy gave me a list of problems, but said that he didn’t expect me to solve all of them — just a few. The problems were so difficult that he wanted to sit with me and read them together to make sure that I understood them.

The problems were Olympiad style, which is my forte. While we were reading them, I solved half of them. During the next hour I solved the rest. The interviewer was stunned. He told me of an additional problem that he and his colleagues had been trying to solve for a long time and couldn’t. He asked me to try. I solved that one as well. Guess what? I wasn’t hired. Hence, my reaction to my friend’s interview.

The good news: I still remember the problem they couldn’t solve:

A car is on a circular road that has several gas stations. The gas stations are running low on gas and the total amount of gas available at the stations and in the car is exactly enough for the car to drive around the road once. Is it true that there is a place on the road where the car can start driving, stopping to refuel at each station, so that the car completes a full circle without running out of gas? Assume that the car’s tank is large enough not to present a limitation.

Share:

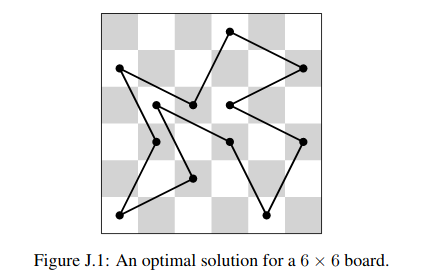
Sid Dhawan was one of our RSI 2011 math students. He was studying interlocking polyominoes under the mentorship of Zachary Abel.

A set of polyominoes is interlocked if no subset can be moved far away from the rest. It was known that polyominoes that are built from four or fewer squares do not interlock. The project of Dhawan and his mentor was to investigate the interlockedness of larger polyominoes. And they totally delivered.

They quickly proved that you can interlock polyominoes with eight or more squares. Then they proved that pentominoes can’t interlock. This left them with a gray area: what happens with polyominoes with six or seven squares? After drawing many beautiful pictures, they finally found the structure presented in our accompanying image. The system consists of 12 hexominoes and 5 pentominoes, and it is rigid. You cannot move a thing. That means that hexominoes can be interlocked and thus the gray area was resolved.

You can find the proofs and the details in their paper “Complexity of Interlocking Polyominoes”. As you can guess by the title, the paper also discusses complexity. The authors proved that determining interlockedness of a a system that includes hexominoes or larger polyominoes is PSPACE hard.Share:

My son Sergei invented the following game a couple of years ago. Two people, Alice and Bob, agree on a number, say, four. Alice takes a clean Rubik’s cube and secretly makes four moves. Bob gets the resulting cube and has to rotate it to the initial state in not more than four moves. Bob doesn’t need to retrace Alice’s moves. He just needs to find a short path back, preferably the shortest one. If he is successful, he gets a point and then it is Alice’s turn.

If they are experienced at solving Rubik’s cube, they can increase the difficulty and play this game with five or six moves.

By the way, how many moves do you need to solve any position on a Rubik’s cube if you know the optimal way? The cube is so complicated that people can’t always know the optimal way. They think that God can, so they called the diameter of the set of all possible Rubik’s cube positions, God’s Number. It was recently proven that God’s Number is 20. If Alice and Bob can increase the difficulty level to 20, that would mean that they can find the shortest path back to the initial state from any position of the cube, or, in short, that they would master God’s algorithm.Share:

I recently published my new favorite math problem:

A deck of 36 playing cards (four suits of nine cards each) lies in front of a psychic with their faces down. The psychic names the suit of the upper card; after that the card is turned over and shown to him. Then the psychic names the suit of the next card, and so on. The psychic’s goal is to guess the suit correctly as many times as possible.
The backs of the cards are asymmetric, so each card can be placed in the deck in two ways, and the psychic can see which way the top card is oriented. The psychic’s assistant knows the order of the cards in the deck; he is not allowed to change the order, but he may orient any card in either of the two ways.
Is it possible for the psychic to make arrangements with his assistant in advance, before the latter learns the order of the cards, so as to ensure that the suits of at least (a) 19 cards, (b) 23 cards will be guessed correctly?
If you devise a guessing strategy for another number of cards greater than 19, explain that too.

If the psychic is only allowed to look at the backs of the cards, then the amount of transmitted information is 2³⁶, which is the same amount of information as suits for 18 cards. This number of guesses is achievable: the backs of every two cards can clue in the suit of the second card in the pair. This way the psychic can guess the suits of all even-numbered cards in the deck. So the problem is to improve on that. Using the info from the cards that the psychic is permitted to turn over can help too.

The problem is from the book Moscow Mathematical Olympiads, 2000-2005. The book and Russian blog discussions provide many different ideas on how to guess more than half of the deck.

Here is the list of ideas.

Idea 1. Counting cards. If you count cards you will know the suits of the last cards.

Idea 2. Trading. As we discussed before, the psychic can correctly guess the suits of even-numbered cards. By randomly guessing the odd-numbered cards she can correctly guess on average the suits of 4.5 additional cards. Unfortunately, this is not guaranteed. But wait. What if we trade the knowledge of the second card’s suit for the majority suit among odd-numbered cards?

Idea 3. Three cards. Suppose we have three cards. Three bits can provide the following knowledge: the majority color, plus the suit of the first and of the second cards in the majority color. Thus, three bits of information will allow the psychic to guess the suits of two cards out of three.

Idea 4. Which card. Suppose the assistant signals the suits of even-numbered cards. With no loss, the psychic can guess the even-numbered card and repeat the same suit for the next card. If this is the plan, the assistant can choose which of the two cards to describe. Which card of the two matches the psychic’s guess provides an additional bit of information.

Idea 5. Surprise. Suppose we have a strategy to inform the psychic about some cards. Suppose the assistant deliberately fails on one of the cards. Then the index of this card provides info to the psychic.

I leave it to my readers to use these ideas to find the solution for 19, 23, 24 and maybe even for 26 cards.Share:

I recently posted an essay Binary Bulls without Cows with the following puzzle:

The test Victor is taking consists of n “true” or “false” questions. In the beginning, Victor doesn’t know any answers, but he is allowed to take the same test several times. After completing the test each time, Victor gets his score — that is, the number of his correct answers. Victor uses the opportunity to re-try the test to figure out all the correct answers. We denote by a(n) the smallest numbers of times Victor needs to take the test to guarantee that he can figure out all the answers. Prove that a(30) ≤ 24, and a(8) ≤ 6.

There are two different types of strategies Victor can use to succeed. First, after each attempt he can use each score as feedback to prepare his answers for the next test. Such strategies are called adaptive. The other type of strategy is one that is called non-adaptive, and it is one in which he prepares answers for all the tests in advance, not knowing the intermediate scores.

Without loss of generality we can assume that in the first test, Victor answers “true” for all the questions. I will call this the base test.

I would like to describe my proof that a(30) ≤ 24. The inequality implies that on average five questions are resolved in four tries. Suppose we have already proven that a(5) = 4. From this, let us map out the 24 tests that guarantee that Victor will figure out the 30 correct answers.

As I mentioned earlier, the first test is the base test and Victor answers every question “true.” For the second test, he changes the first five answers to “false,” thus figuring out how many “true” answers are among the first five questions. This is equivalent to having a base test for the first five questions. We can resolve the first five questions in three more tests and proceed to the next group of five questions. We do not need the base test for the last five questions, because we can figure out the number of “true” answers among the last five from knowing the total score and knowing the answers for the previous groups of five. Thus we showed that a(mn) ≤ m a(n). In particular, a(5) = 4 implies a(30) ≤ 24.

Now I need to prove that a(5) = 4. I started with a leap of faith. I assumed that there is a non-adaptive strategy, that is, that Victor can arrange all four tests in advance. The first test is TTTTT, where I use T for “true” and F for “false.” Suppose for the next test I change one of the answers, say the first one. If after that I can figure out the remaining four answers in two tries, then that would mean that a(4) = 3. This would imply that a(28) ≤ 21 and, therefore, a(30) ≤ 23. If this were the case, the problem wouldn’t have asked me to prove that a(30) ≤ 24. By this meta reasoning I can conclude that a(4) ≠ 3, which is easy to check anyway. From this I deduced that all the other tests should differ from the base test in more than one answer. Changing one of the answers is equivalent to changing four answers, and changing two answers is equivalent to changing three answers. Hence, we can assume that all the other tests contain exactly two “false” answers. Without loss of generality, the second test is FFTTT.

Suppose for the third test, I choose both of my “false” answers from among the last three questions, for example, TTFFT. This third test gives us the exactly the same information as the test TTTTF, but I already explained that having only one “false” answer is a bad idea. Therefore, my next tests should overlap with my previous non-base tests by exactly one “false” answer. The third test, we can conclude, will be FTFTT. Also, there shouldn’t be any group of questions that Victor answers the same for every test. Indeed, if one of the answers in the group is “false” and another is “true,” Victor will not figure out which one is which. This uniquely identifies the last test as FTTFT.

So, if the four tests work they should be like this: TTTTT, FFTTT, FTFTT, FTTFT. Let me prove that these four tests indeed allow Victor to figure out all the answers. Summing up the results of the last three tests modulo 2, Victor will get the parity of the number of correct answers for the first four questions. As he knows the total number of correct answers, he can deduce the correct answer for the last question. After that he will know the number of correct answers for the first four questions and for every pair of them. I will leave it to my readers to finish the proof.

Knop and Mednikov in their paper proved the following lemma:

If there is a non-adaptive way to figure out a test with n questions by k tries, then there is a non-adaptive way to figure out a test with 2n + k − 1 questions by 2k tries.

Their proof goes like this. Let’s divide all questions into three non-overlapping groups A, B, and C that contain n, n, and k − 1 questions correspondingly. By our assumptions there is a non-adaptive way to figure out the answers for A or B using k tries. Let us denote subsets from A that we change to “false” for k − 1 non-base tests as A₁, …, A_k-1. Similarly, we denote subsets from B as B₁, …, B_k-1.

Our first test is the base test that consists of all “true” answers. For the second test we change the answers to A establishing how many “true” answers are in A. In addition we have k − 1 questions of type Sum: we switch answers to questions in A_i ∪ B_i ∪ C_i; and type Diff: we switch answers to (A ∖ A_i) ∪ B_i. The parity of the sum of “false” answers in A − A_i + B_i and A_i + B_i + C_i is the same as in A plus C_i. But we know A‘s score from the second test. Hence we can derive C_i. After that we have two equations with two unknowns and can derive the scores of A_i and B_i. From knowing the number of “true” answers in A and C, we can derive the same for B. Knowing A and A_i gives all the answers in A. Similarly for B. QED.

This lemma is powerful enough to answer the original puzzle. Indeed, a(2) = 2 implies a(5) ≤ 4, and a(3) = 3 implies a(8) ≤ 6.Share:

The following variation of a Bulls and Cows problem was given at the Fall 2008 Tournament of the Towns:

A test consists of 30 true or false questions. After the test (answering all 30 questions), Victor gets his score: the number of correct answers. Victor doesn’t know any answer, but is allowed to take the same test several times. Can Victor work out a strategy that guarantees that he can figure out all the answers after the 29th attempt? after the 24th attempt?

Let’s assume that we have a more general problem. There are n questions, and a(n) is the smallest number of times we need to take the test to guarantee that we can figure out the answers. First we can try all combinations of answers. This way we are guaranteed to know all the answers after 2ⁿ attempts. The next idea is to start with a baseline test, for example, to say that all the answers are true. Then we change answers one by one to see if the score goes up or down. After changing n − 1 answers we will know the answers to the first n − 1 questions. Plus we know the total number of true answers, so we know the answers to all the questions. We just showed that a(n) ≤ n.

This is not enough to answer the warm-up question in the problem. We need something more subtle.

Let’s talk about the second part of the problem. As we know, 24 = 4 ⋅ 6. So to solve the second part, on average, we need to find five correct answers per four tests. Is it true that a(5) ≤ 4? If so, can we use it to show that a(30) ≤ 24?

The following three cases are the most fun to prove: a(5) = 4, a(8) ≤ 6, and a(30) ≤ 24. Try it!

By the way, K. Knop and L. Mednikov wrote a paper (available in Russian) where they proved that a(n) is not more than the smallest number k such that the total number of ones in the binary expansion of numbers from 1 to k is at least n − 1. Which means they proved that a(30) ≤ 16.Share: