15th November 2012, 02:34 pm
One of the 2012 PRIMES projects, suggested by Professor Jacob Fox, was about bounds on the number of halving lines. I worked on this project with Dai Yang.
Suppose there are n points in a general position on a plane, where n is an even number. A line through two given points is called a halving line if it divides the rest of n−2 points in half. The big question is to estimate the maximum number of halving lines.
Let us first resolve the small question: estimating the minimum number of halving lines. Let’s take one point from the set and start rotating a line through it. By a continuity argument you can immediately see that there should be a halving line through any point. Hence, the number of halving lines is at least n/2. If the point is on the convex hull of the set of points, then it is easy to see that it has exactly one halving line through it. Consequently, if the points are the vertices of a convex n-gon, then there are exactly n/2 halving lines. Thus, the minimum number of halving lines is n/2.
Finding the maximum number of halving lines is much more difficult. Previous works estimated the upper bound by O(n4/3) and the lower bound by O(ne√log n). I think that Professor Fox was attracted to this project because the bounds are very far from each other, and some recent progress was made by elementary methods.
Improving a long-standing bound is not a good starting point for a high school project. So after looking at the project we decided to change it in order to produce a simpler task. We decided to study the underlying graph of the configuration of points.
Suppose there is a configuration of n points on a plane, and we are interested in its halving lines. We associate a graph to this set of points. A vertex in the configuration corresponds to a vertex in the graph. The graph vertices are connected, if the corresponding vertices in the set have a halving line passing through them. So we decided to answer as many questions about the underlying graph as possible.
For example, how long can the longest path in the underlying graph be? As I mentioned, the points on the convex hull have exactly one halving line through them. Hence, we have at least three points of degree 1, making it impossible for a path to have length n. The picture below shows a configuration of eight points with a path of length seven. We generalized this construction to prove that there exists a configuration with a path of length n−1 for any n.
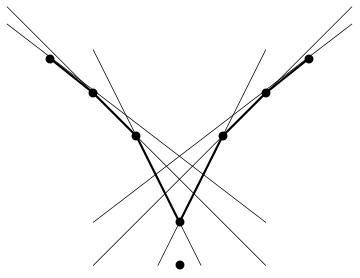
We also proved that:
- The largest cycle can have length n − 3.
- The largest clique is of the order O(√n).
- The degrees of two distinct vertices sum to at most n, if they are connected by an edge, and at most n − 2 otherwise.
After we proved all these theorems, we came back to the upper bound and improved it by a constant factor. Our paper is available at arXiv:1210.4959.
Share:





12th November 2012, 03:27 pm
Samuel Hansen has an unusual profession: he is a mathematics podcaster. He interviewed me for his Relatively Prime podcast titled 0,1,2,3,…, where we discussed my Number Gossip project. The podcast also includes interviews with Neil Sloane, Michael Shamos, and Alex Bellos.
My previous interview with Samuel is at acmescience.com. There I discuss both math education and gender in math issues.
When I listened to myself, I found it strange that I seemed to have a British accent on top of my Russian accent. Did you notice that too?
Share:





10th November 2012, 09:58 am
I discovered the following chess puzzle on a Russian blog for puzzle lovers. It is a helpmate-type puzzle. Black cooperates with White in checkmating himself. In this particular puzzle Black starts and helps White to win in one move.
Oops. Something is not quite right. There are not enough pieces on the board. To recover the missing pieces in order to solve the puzzle, you need to retrace your steps. If Black and White go back one move each, they will be able to cooperatively checkmate Black in one move. Find the position one move back and the cooperative checkmate.
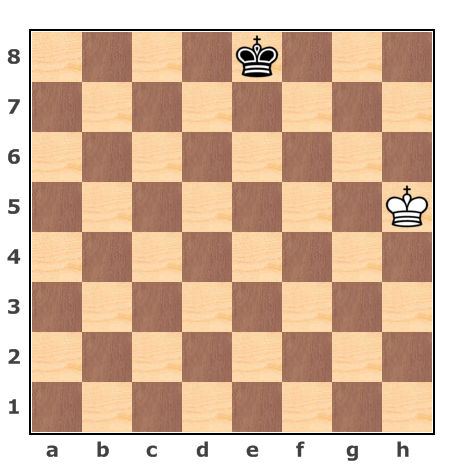
Share:





10th November 2012, 09:51 am
I am Russian; I know how to play chess. My father taught me when I was three or four. We played a lot and he would always win. I got frustrated with that and one day, when I was five, I didn’t announce my check. On the next move, I grabbed his king and claimed my victory.
He was so angry that he turned red and almost hit me. This frightened me so much that I lost my drive for chess that very moment.
I still understand its beauty and solve a chess problem about once a decade. Look for a cute chess puzzle in my next post.
Share:





7th November 2012, 04:03 pm
For my every class I try to prepare a challenge problem to stretch the minds of my students. Here is a problem I took from Adam A. Castello’s website:
There is a ceiling a hundred feet above you that extends for- ever, and hanging from it side-by-side are two golden ropes, each a hundred feet long. You have a knife, and would like to steal as much of the golden ropes as you can. You are able to climb ropes, but not survive falls. How much golden rope can you get away with, and how? Assume you have as many hands as you like.
The next problem I heard from my son Sergei:
You are sitting at the equator and you have three planes. You would like to fly around the equator. Each plane is full of gas and each has enough gas to take you half way around. Planes can transfer gas between themselves mid-air. You have friends, so that you can fly more than one plane at once. How do you fly around the equator?
Share:





7th November 2012, 03:23 pm
* * *
Right clicking a file with a mouse will allow you to change it, check it for viruses, or revert to the previous version. I wonder where I can buy a mouse that can do the same thing with my husband.
* * *
— Let’s have sex.
— Sure, but today I want to be the numerator.
* * *
Attention! We want to check that you are not a robot. Please, undress and turn on a web-camera.
* * *
In a drug store:
— I would like input and output cleaners.
— ???
— Toothpaste and toilet paper.
* * *
I used to recount the multiplication tables to delay my ejaculation. Now, each time I see the multiplication tables I get a hard on.
* * *
— Tonight my parents are away. Let’s finally try a forbidden thing.
— Dividing by zero?
* * *
My friend put his mistress in his phone’s contact list as ‘low battery’.
Share:





3rd October 2012, 08:24 pm
3rd October 2012, 10:05 am
I would like to report on my weight loss progress. Last time I added two new habits, walking my toy dog every day, and drinking more water from the enticing cute bottles I bought.
I named my stuffed dog Liza and I walk with her every day. I didn’t expect immediate weight loss due to this new regime, because my first goal was to get out of the house every day, even if only for two seconds. The next step will be to increase walking time to ten minutes.
Drinking a lot of water doesn’t work well. I spend too much time looking for bathrooms and panicking that I will not make it. I like the idea of drinking a lot of water, but I am not sure I can hold to it, if you understand what I mean.
Since taking on this challenge, I’ve gained two habits, but I haven’t lost a pound.
Now I’m upping my game. Below is my analysis of why I eat. When I eat, I believe that I am hungry. But looking at this more objectively I think this is not always the case: sometimes there are other reasons. I am listing these other reasons so I can fight them face-to-face. Here we go:
- I eat to finish what is on my plate. My mom lived through World War II in Moscow, and instilled in me a terrible guilt when I throw away food.
- I eat extra when I do not know when my next meal is. I experienced extreme hunger in my childhood, so I try to prevent ever having that terrible feeling again.
- I can’t resist free food. I do not feel comfortable with my financial situation, so saving money gives me an extra push to eat even when I’m not hungry.
- I procrastinate by eating. When I am facing a chore I don’t really want to do, I delay it by eating.
- I crave sugar. It used to be worse.
- I have a problem with delicious food. I think that deep inside I feel that life was unfair to me and this piece of tiramisu will be a small bright spot in my usually rainy life. Therefore I need to grab it and gobble it down before it disappears.
Hmm. That was painful to write. My psychoanalyst taught me that pain means I am on the right track.
Share:





2nd October 2012, 08:33 am
Davidson Institute for Talent Development announced their 2012 Winners. Out of 22 students, three were recognized for their math research. All three of them are ours: that is, they participated in our PRIMES and RSI programs:
- David Ding’s project, “Infinitesimal Cherednik Algebras of gln,” came out of his participation in the PRIMES program.
- Sitan Chen’s project, “On the Rank Number of Grid Graphs,” came out of his participation in the RSI program.
- Xiaoyu He’ project, “On the Classification of Universal Rotor-Routers,” came out of his participation in the PRIMES program.
I already wrote about Xiaoyu’s project. Today I want to write about Sitan’s project and what I do as the math coordinator for RSI.
RSI students meet with their mentors every day and I meet with students once a week. On the surface I just listen as they describe their projects. In reality, I do many different things. I cheer the students up when they are overwhelmed by the difficulty of their projects. I help them decide whether they need to switch projects. I correct their mistakes. Most projects involve computer help, so I teach them Mathematica. I teach them the intricacies of Latex and Beamer. I explain general mathematical ideas and how their projects are connected to other fields of mathematics. I never do their calculations for them, but sometimes I suggest general ideas. In short, I do whatever needs to be done to help them.
I had a lot of fun working with Sitan. His project was about the rank number of grid graphs. A vertex k-ranking is a labeling of the vertices of a graph with integers from 1 to k so that any path connecting two vertices with the same label passes through a vertex with a greater label. The rank number of a graph is the minimum possible k for which a k-ranking exists for that graph. When Sitan got the project, the ranking numbers were known for grid graphs of sizes 1 by n, 2 by n, and 3 by n. So Sitan started working on the ranking number of the 4 by n graph.
His project was moving unusually fast and my job was to push him to see the big picture. I taught him that the next step, once he finishes 4 by n graphs is not to do 5 by n graphs, as one might think. After the first step, the second step should be bigger. He should use his insight and understanding of 4 by n graphs to try to see what he can do for any grid graphs.
This is exactly what he did. After he finished the calculation of the rank number of the 4 by n graphs, he found a way to improve the known bounds for the ranking number of any grid graph. His paper is available at the arXiv.
I just looked at my notes for my work with Sitan. The last sentence: “Publishable results, a potential winner.”
Share:





30th September 2012, 09:06 am
PRIMES-USA: A new MIT program for talented math students from across the country.
I’ve been working as a math coordinator for RSI, the most competitive summer program for high school juniors. RSI arranges for these select students to do scientific research. I only work with kids who do math, and usually we have a dozen of them. Every student has an individual mentor, usually a graduate student, with whom they meet daily. I supervise all the projects and meet with each high school student about once a week. My job was described as “going for the biggest impact”: when the project is in trouble, I jump in to sort it out; when the project is doing well, I push it to further limits.
RSI is a great program: kids enjoy it and we produce interesting research. My biggest concern is that the program is too short. The kids do math for five weeks and they usually approach a good result, but at the end of RSI we generally see just a hint of what they could truly achieve. Kids who continue to work on their own after the program ends are more successful. Unfortunately most of the students stop working at the end of the program just as they are approaching a big theorem.
I discussed this dissatisfying trend with Pavel Etingof and Slava Gerovitch and we decided to do something about it. Pavel and Slava conceived and found funding for a new program called PRIMES that is similar to RSI, but runs for a year. From February through May, PRIMES students meet with their mentors weekly. In fact, we require on the application that the students commit to coming to MIT once a week, thereby limiting us to local students. Theoretically, someone from Detroit with a private jet who can fly to MIT weekly would be welcomed.
Before the first year, we wondered whether the smaller pool of local students would be weaker than national and international RSI students. To our delight, that wasn’t the case. In the first year we got fantastic students. One explanation is that PRIMES is much more flexible. We do not mind when our students go to IMO in the summer or to math camps or when they go away on vacation with their parents. As a result, we get students who would never apply to RSI because of their summer schedules. Our PRIMES students have won so many prizes that I do not remember them all. We post our successes on the website.
Our success in PRIMES suggests that there are likely many talented kids in other states who never even apply to RSI because of a scheduling conflict. This led us to try to adapt PRIMES to national needs. So we created a new program called PRIMES-USA that will accept students from across the country. We will work with them through Skype. These students must commit to travel to MIT for a PRIMES conference in May. Because this is our pilot program, we will only accept five students.
Share:






