I am Hooked on Star Battles
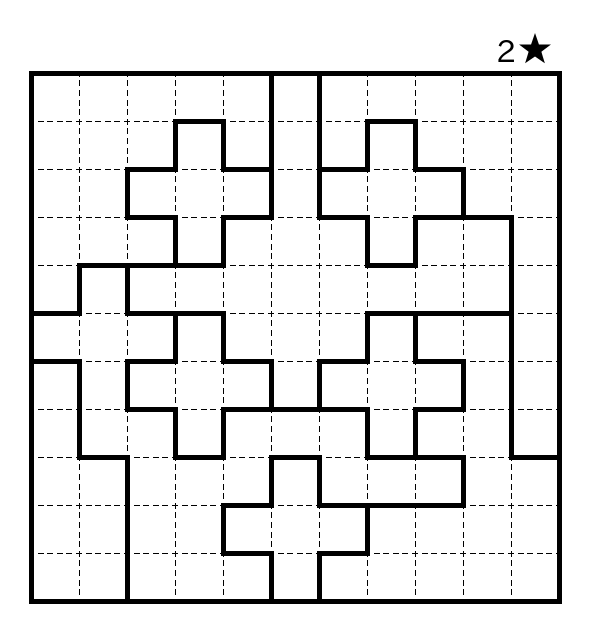
I recently published Sergei Bernstein’s awesome Star Battle called Swiss Cheese. Another lovely Star Battle from him is called Hooks. You can play it online at puzz.link.
Share:
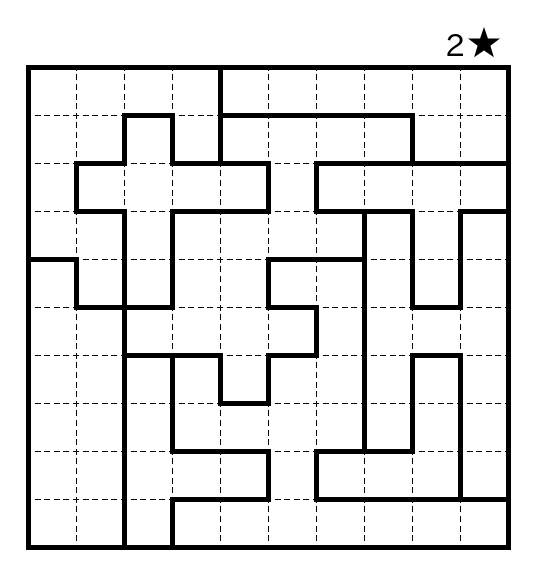
Swiss Cheese Star Battle
Star Battle is one of my favorite puzzle types. The rules are simple: put two stars in each row, column, and bold region (one star per cell). In addition, stars cannot be neighbors, even diagonally.
My son, Sergei Bernstein, recently designed a Star Battle with a beautiful solve path. This is my favorite Star Battle so far. I like its title too: Swiss Cheese.
You can also solve it at the puzz.link Star Battle player.
Share:
Our Familect Story
A familect is a portmanteau word formed by squashing together two words: family and dialect. It means words that a family uses that are not a part of a standard vocabulary. This story is about two words that my son Sergei invented, and twenty years later, my family still uses them.
As you might know, I was married three times, and I have two sons, from two different fathers. These fathers were also married several times and had other children. My two sons are half-brothers, and they also have half-siblings through their fathers. Thus a half-sister of a half-brother became a quarter-sister. Inventing this term was quite logical for a son of two mathematicians.
As you can imagine, our family tree is complicated. One day Sergei pointed out that our tree doesn’t look like a standard tree and called it a family bush.
Share:I Miss John Conway
Yesterday I stumbled upon a picture of John Conway I completely forgot I had: it was saved in a wrong folder. The photo was taken at the MOVES conference in 2015. There is a third person in the original shot, but I do not remember her. I decided to cut her out as I didn’t know how to contact her for permission to post this photo.

Share:
The Anniversary Coin
Konstantin Knop, the world’s top authority on coin-weighing puzzles, suggested the following problem for the 2019 Russian Math Olympiad.
Share:Puzzle. Eight out of sixteen coins are heavier than the rest and weigh 11 grams each. The other eight coins weigh 10 grams each. We do not know which coin is which, but one coin is conspicuously marked as an “Anniversary” coin. Can you figure out whether the Anniversary coin is heavier or lighter using a balance scale at most three times?
Build an All-red Cube
This is one of my favorite problems given at the 2017 Moscow Olympiad to grades 6 and 7. It was suggested by one of my favorite problem writers: Alexander Shapovalov.
Share:Problem. We are given eight unit cubes. The third of the total number of their faces are blue, and the rest are red. We build a large cube out of these cubes so that exactly the third of the unit cube’s visible faces are red. Prove that you can use these cubes to build a large cube whose faces are entirely red.
Penney’s Game and Groups
For the last year, I’ve been obsessed with Penney’s game. In this game, Alice picks a string of coin tosses, say HHH for three heads. After that, Bob picks his string of tosses of the same lengths, say HTH. Then they toss a fair coin. The person whose string shows up first wins. For example, if the tosses are THTTHHH, then Alice wins after the seventh toss. For these particular choices, Bob wins with probability 3/5.
With my PRIMES student, Sean Li, we looked at this game and asked a different question. Suppose Alice picks a pattern of three tosses in a row that are the same. Suppose after that, Bob chooses a pattern of three alternating tosses. Then they toss a fair coin. Alice is hoping for HHH or TTT, while Bob is hoping for HTH or THT. The person whose pattern shows up first wins. For example, if the tosses are THTTHHH, then Bob wins after the third toss. For these particular choices, Bob wins with probability 1/2.
In this example, what actually happens. We assume that the group of two elements acts on the alphabet of two letters. The group’s non-identity element swaps letters H and T. We assume that two strings are equivalent if they belong to the same equivalency class under the group action. We call such an equivalency class a pattern.
In the new game we invented, we have an alphabet of any size and any group acting on the alphabet. Then Alice and Bob pick their patterns. After that, they play the Penney’s game on these patterns. The answers to all the relevant questions are in our paper, The Penney’s Game with Group Action, posted at the math.CO arxiv 2009.06080.
Share: