15th December 2021, 02:06 pm
Today I present three problems from the 41-st Tournament of the Towns that I liked: an easy one, one that reminds me of the Collatz conjecture, and a hard one.
Problem 1 (by Aleksey Voropayev). A magician places all the cards from the standard 52-card deck face up in a row. He promises that the card left at the end will be the ace of clubs. At any moment, an audience member tells a number n that doesn’t exceed the number of cards left in the row. The magician counts the nth card from the left or right and removes it. Where does the magician need to put the ace of clubs to guarantee the success of his trick?
Problem 2 (by Vladislav Novikov). Number x on the blackboard can be replaced by either 3x + 1 or ⌊x/2⌋. Prove that you can use these operations to get to any natural number when starting with 1.
Problem 3 (by A. Gribalko). There are 2n consecutive integers written on a blackboard. In one move, you can split all the numbers into pairs and replace every pair a, b with two numbers: a + b and a − b. (The numbers can be subtracted in any order, and all pairs have to be replaced simultaneously.) Prove that no 2n consecutive integers will ever appear on the board after the first move.
Share:





14th December 2021, 06:29 pm
Here is a cute old problem that Facebook recently reminded me of.
Puzzle. By mistake, a clock-maker made the hour hand and the minute hand on a clock exactly the same. How many times a day, you can’t tell the current time by looking at the clock? (It is implied that the hands move continuously, and you can pinpoint their exact location. Also, you are not allowed to watch how the hands move.)
Here is the solution by my son who was working on it together with my grandson.
The right way to think about it is to imagine a “shadow minute hand”, like this: Start at noon. As the true hour hand advances, the minute hand advances 12 times faster. If the true minute hand were the hour hand, there would have to be a minute hand somewhere; call that position the shadow minute hand. The shadow minute hand advances 12 times faster than the true minute hand. The situations that are potentially ambiguous are the ones where the shadow minute hand coincides with the hour hand. Since the former makes 144 circuits while the latter makes 1, they coincide 143 times. However, of those, 11 are positions where the true minute hand is also in the same place, so you can still tell the time after all. So there are 132 times where the time is ambiguous during the 12-hour period, which leads to the answer: 268.
I love the problem and gave it to my students; but, accidentally, I used CAN instead of CAN’T:
Puzzle. By mistake, a clock-maker made the hour hand and the minute hand on a clock exactly the same. How many times a day can you tell the current time by looking at the clock?
Obviously, the answer is infinitely many times. However, almost all of the students submitted the same wrong finite answer. Can you guess what it was? And can you explain to me why?
Share:





11th December 2021, 02:36 pm
5th December 2021, 11:03 am
A cute puzzle found on Facebook:
Puzzle. Four wizards A, B, C, and D, were given three cards each. They were told that the cards had numbers from 1 to 12 written without repeats. The wizards only knew their own three numbers and had the following exchange.
- A: “I have number 8 on one of my cards.”
- B: “All my numbers are prime.”
- C: “All my numbers are composite. Moreover, they all have a common prime factor.”
- D: “Then I know the cards of each of you.”
Given that every wizard told the truth, what cards does A have?
Share:





28th November 2021, 01:54 pm
* * *
I surveyed many people who had played Russian roulette. Seems like the probability of dying is actually 0%.
* * *
What has the probability of one in five million?
Zero: there’s no 1 in 5000000. Only a five and six zeros.
* * *
Two classmates:
—What did you think of our probability exam yesterday?
—All means to an end.
* * *
My classmate didn’t study for our test in probability.
“I’ll take my chances”, he said.
* * *
I saw my math teacher with a piece of graph paper yesterday. I think he must be plotting something.
* * *
Not all math puns are terrible. Just sum.
* * * (submitted by Sergei Bernstein)
A programmer walks into a bar, holds up two fingers, and says, “I’ll have three beers please.”
* * *
What is the similarity between me and an experiment involving a biased coin with two tails?
The probability of getting a head is zero.
Share:





27th November 2021, 01:06 pm
I’ve been crocheting hyperbolic surfaces of constant curvature. The process is time-consuming, so while I am crocheting, I wonder about the mathematics of crocheting.
Hilbert’s theorem says that I can’t embed a hyperbolic plane in 3-dimensional space. The proof is rather involved. But here, I have an explanation from the point of view of a crochet hook. My hook starts with a tiny cycle of four stitches. Then for every x stitches the hook makes y stitches in the next row, where y is greater than x. The extra stitches should be evenly distributed to guarantee that locally every small area is approximately isomorphic to other areas, meaning that the surface has a constant curvature.
The ratio of stitches in the next row to the current row is r = y/x. Thus, the number of stitches in each row increases exponentially. But each row is a fixed height h. That means after k rows, my thingy has to fit inside a ball of radius kh. But the length of the last row is 4rk-1. It becomes huge very fast. As the last row is a physical curve made out of stitches, there is a limit of how much of it I can fit into a given volume, creating a contradiction.
That means, if I start crocheting, something should happen that won’t allow me to continue. I decided to experiment and see what actually would happen. Being lazy, I preferred the disaster to happen sooner rather than later. So I chose the ratio of three: for each stitch on my perimeter, I added three new stitches. Shortly after I started to work, the process became more and more difficult. The ball was too tight. It was challenging to hold that thing in the place where I needed to insert the hook. And the loops were getting tighter, making it more exhausting to insert the hook into the proper hole. So each new stitch was taking more and more time to complete.
To my disappointment, the thing didn’t explode, as I was secretly hoping: I just couldn’t work on it anymore.
Share:





15th October 2021, 03:24 pm
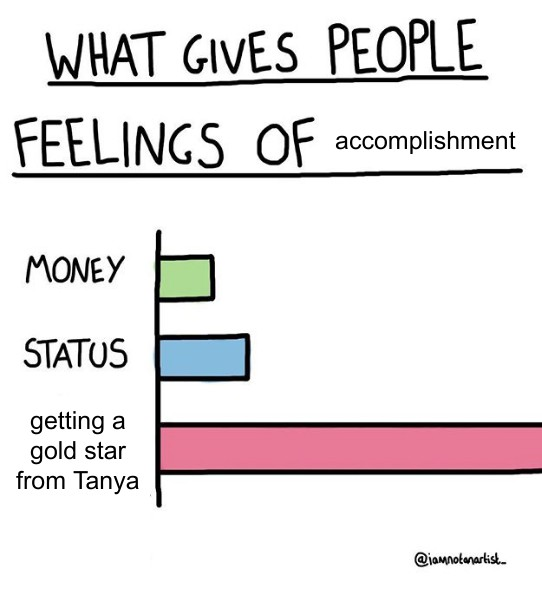
I like rewarding my students. Before covid, I used to give them star stickers for good ideas. When I started to teach remotely, I wondered what I should do instead. I could tell them that they had won a star, but it felt too weak. The next idea was to show them a star and tell them that it belonged to them. But that still felt insufficient. Then I had an epiphany. I would say to them they earned a star, show it to them, and stick it to my face. So they, and all the other students, would see it for the rest of the class. The photo shows how I looked at the end of a successful lesson.
Another picture shows what my MathRoots students posted on our Discord channel.
Now that I am back teaching in person, my students asked me to continue sticking their stars to my face. Sometimes I forget about the stars and, after my class, wander around MIT star-covered.
Share:





27th September 2021, 02:20 pm
My son, Alexey Radul, wrote a program that finds the largest numbers to start a sequence in the Online Encyclopedia of Integer Sequences (OEIS). To my surprise, the top ten are all numbers consisting of ones only. The largest number is 11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111: a number with 128 ones. The sequence is A095646: a(n) is 128 written in base n. It starts with base 1, or more precisely, the unary expansion, which indeed requires 128 ones to express the number 128.
I decided to expand my top list to 50. Again, most of the numbers are bunches of ones: 48 out of the top 50 numbers are unary expansions of numbers 81 through 128. There are two more numbers in the top 50 that are different and belong to awesome sequences.
The first awesome sequence is sequence A033290: Ten consecutive primes in arithmetic progression. It starts with the number 100996972469714247637786655587969840329509324689190041803603417758904341703348882159067229719, which has 93 digits. This number takes 37th place on my list.
The second awesome sequence is sequence A291042: One powerful arithmetic progression with a nontrivial difference and maximal length. The sequence corresponds to a cool puzzle that appeared in the American Mathematical Monthly in 2000. The question was, “What is the length of the longest non-constant arithmetic progression of integers with the property that the kth term is a perfect kth power?” The answer is 5. John P. Robertson proved that such progression can’t have 6 terms and provided an example of a sequence with 5 terms, which is the sequence in the OEIS.
Here is how to construct this sequence. Start with an arithmetic progression 1, 9, 17, 25, 33, and multiply each term by 32453011241720: the result is also an arithmetic progression. The first term is trivially a first power. The second term is 32653011241720 = (31351511121710)2 and a square. The third term is 32453011241721 = (38510118177)3 and a cube. The fourth term is 32453211241720 = (3658116175)3 and a fourth power. The fifth term is 32553011251720 = (3556115174)5 and a fifth power.
The sequence starts with the number 10529630094750052867957659797284314695762718513641400204044879414141178131103515625. It has 83 digits, and it takes 48th place on my list.
Share:





19th September 2021, 05:30 pm
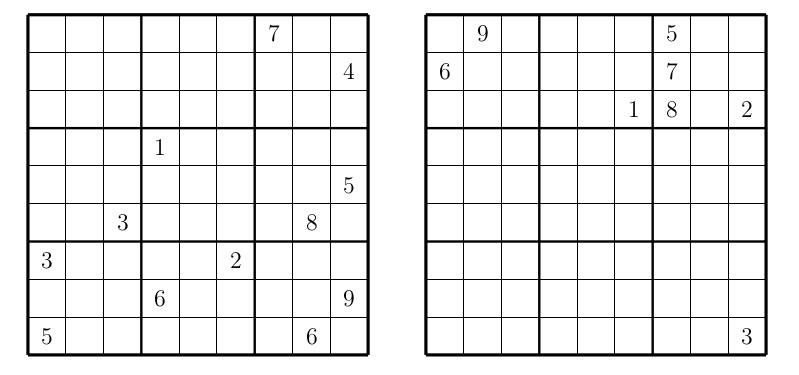
My students (Matvey Borodin, Eric Chen, Aidan Duncan, Boyan Litchev, Jiahe Liu, Veronika Moroz, Matthew Qian, Rohith Raghavan, Garima Rastogi, Michael Voigt) and I recently wrote a paper connecting the stable marriage problem and Sudoku. I just blogged about it. By the way, my students are in grades 7-9.
On the way, we invented a new type of Sudoku, which we call joint-groups Sudoku. This type is in contrast to a famous type of Sudoku, called disjoint-groups Sudoku. In a disjoint-groups Sudoku, in a particular place in a 3 by 3 box, all the digits are distinct across all the boxes. For example, the top-left corners of nine boxes have all the digits 1 thought 9. This creates nine additional disconnected regions (depending on the placements inside a 3 by 3 box) to add to columns, rows, and boxes that have to contain distinct digits.
For our new type, we wanted the digits in a particular place in each box, instead of being different, to be the same as much as possible. How much of sameness is possible? The first row contains three top-left corners. Thus, by Sudoku rules, these top-left corners have to be distinct. Thus, the top-left corners in all nine boxes have to contain at least three distinct digits. So here is the rule for the joint-groups Sudoku: the nine digits in a particular place in a 3 by 3 box contain not more than three distinct digits. It is easy to see that it means they contain exactly 3 distinct digits, each of them three times.
Here are two Sudoku puzzles from our paper. Each puzzle, when completed, forms a joint-groups Sudoku.
Share:





3rd September 2021, 05:53 pm
As you may know, I run PRIMES STEP, a local program where we do mathematical research with students in grades 6-9. Last academic year, we looked at the stable marriage problem and discovered its connection to Sudoku. Our paper The Stable Matching Problem and Sudoku (written jointly with Matvey Borodin, Eric Chen, Aidan Duncan, Boyan Litchev, Jiahe Liu, Veronika Moroz, Matthew Qian, Rohith Raghavan, Garima Rastogi, Michael Voigt) is now available at the arxiv.
Consider 3 men and 3 women who want to be married to each other in heterosexual couples. They rank each other without ties. The resulting 6 permutations of numbers 1, 2, and 3 that describe the six rankings are called the preference profile of this group of people. A matching is unstable if two people would be happier to run away together than to marry into the assigned couples. The two potential runaways are called a rogue couple. A matching is called stable if no rogue couple exists. The Gale-Shapley algorithm, invented by Gale and Shapley, finds a stable matching for any preference profile, implying that stable matching is always possible.
We discovered that preference profiles form a natural bijection with ways to place one digit into a Sudoku grid. So we wrote a paper describing the stable marriage, rogue couples, the Gale-Shapley algorithm, soulmates, and such in terms of Sudoku.
Oops, I forgot to explain who the soulmates are. We invented this term to describe two people who rank each other first. Though it is possible to have several stable matchings for the same preference profile if the soulmates exist, they must always be matched together.
We also invented a new Sudoku type, which I will explain next time.
Share: