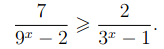Tanya Khovanova's Math Blog

This puzzle was in last week’s homework.

Puzzle. How can an egg fly three meters and not break?

The expected answer:

• The egg flew more than 3 meters and broke afterward.

Some students tried to protect the egg:

• The egg was bubble-wrapped.
• The egg was dropped on a cushion.
• The egg was thrown up, then caught.
• The egg was thrown into water.
• My favorite: The egg used a parachute.

Other students specified qualities of an egg making it more resistant:

• The egg was hard-boiled.
• The egg was made of plastic.
• The egg was a frog egg.
• An educated answer: It could be an ostrich egg, which is extremely strong. (I checked that online, and, indeed, a human can stand on an ostrich egg without breaking it.)
• My favorite: The egg was fried.

Here are some more elaborate explanations:

• The egg flew on a plane.
• The egg was thrown on another planet with low gravity.
• The egg was thrown in space and will orbit the Earth forever.
• My favorite: The egg was not birthed yet: it flew inside a chicken.

To conclude this essay, here is a punny answer:

• The egg was confident, not easy to break by throwing around.

Puzzle. A goat was on a 10-meter leash. Yet it managed to go 300 meters away from the post. How come?

The standard answer. The leash wasn’t attached to the post.

My students scrutinized the puzzle and found some other possible ambiguities. For example, there might be two posts: the goat was leashed to one and was far away from the other. In another example, the timing is not given. It is possible that the goat was on the leash at one time and unleashed and far away from the post at another time. Here is my favorite answer.

My favorite answer. The goat ate the leash.

Here is the current picture of my coauthor, Joel Lewis. I remember him from many years ago when he was a graduate student at MIT. I am glad he kept his big smile.

Back to the subject matter. Joel Lewis made a comment on my recent post, thinking-outside-the-box ideas. He mentioned his two theorems:

The Big Point Theorem. Any three lines intersect at a point, provided that the point is big enough.

The Thick Line Theorem. Any three points lie on the same line, provided that the line is thick enough.

I recently wrote an essay, Thinking Inside and Outside the Box, which starts with a famous nine-dots puzzle that kicked off the expression: thinking outside the box. Here is another puzzle with the same nine-dots setup.

Puzzle. What is the smallest number of squares needed to ensure that each dot is in its own region?

Usually, people who try to solve this puzzle come up with the following four-squares solution.

As with the classic nine-dots puzzle, they imagine that the dots are on a grid and try to build squares with sides parallel to the grid lines. What would be the outside-the-box idea? The sides of the squares would not need to be parallel to the grid. This way, we can solve the puzzle with three squares.

One of my MathRoots students offered a different and awesome solution also using three squares.

The most famous thinking-outside-the-box puzzle is the Nine-Dots puzzle. This puzzle probably started the expression, “To think outside the box”. Here is the puzzle.

Puzzle. Without lifting the pencil off the paper, connect the nine dots by drawing four straight continuous lines that pass through all the dots.

Most people attempt something similar to the picture below and fail to connect all the dots.

They try to connect the dots with line segments that fit inside the square box around the dots, mentally restricting themselves to solutions that are literally inside the box.

To get to the correct solution, the line segments should be drawn outside this imaginary box.

Do you think that four line segments is the best you can do? Jason Rosenhouse showed me a solution for this puzzle that requires only three lines. Here, the outside-the-box idea is to use the thickness of the dots.

This and many other examples of thinking outside the box are included in my paper aptly titled Thinking Inside and Outside the Box and published in the G4G12 Exchange book.

A section of this paper is devoted to my students, who sometimes give unexpected and inventive solutions to famous puzzles. Here is an example of such a puzzle and such solutions that aren’t in the paper because I collected them after the paper was published.

Puzzle. Three men were in a boat. It capsized, but only two got their hair wet. Why?

The standard answer is the following: One man was bald.

Lucky for me, my creative students suggested tons of other solutions. For example,

• One man was wearing a waterproof helmet.
• The boat capsized on land, and two men had their hair already wet.

My favorite example, however, is the following.

• One man didn’t have a head.

For students applying to PRIMES, we have a question about their research interests. RSI asks a similar question from their applicants.

I am looking at all the submissions, and this essay will help our applicants to get projects that are well-suited for them.

We, at PRIMES and RSI Math, usually have research projects lined up in advance. That means, we are not creating projects to match applicants’ requests. We match existing projects to students’ backgrounds and interests.

If you are applying to one of these programs, here is my advice.

Don’t be too specific about what you want. Suppose you want to study the symmetries of an icosahedron. This request is too narrow: there is a high probability we do not have such a project. How will we match you to a project? Our hope, in this case, is to find clues in your essay. For example, we might discover that you heard a fascinating lecture on icosahedron’s symmetries, which is why you requested the topic. In this case, we assume that another fascinating lecture on a different topic might also excite you, and you will be matched with a random project. But if your description is broader, say, if you write that you like group theory or geometry, your match won’t be as random.

Specify things you do not want. Given our project distribution, you might not get a project in the area that is your first or even your second choice. On the other hand, if you write to us that you hate geometry, it is very easy to find a project without a geometric component. If there is something you definitely do not want, it is advantageous for you to mention it. Be precise about your advanced knowledge. For example, linear algebra is one of the most powerful tools in mathematics. Not surprisingly, we often have projects that require a serious background in linear algebra and specifically look for students who know it. Unfortunately, we often receive inadequate descriptions of students’ backgrounds. Even if you took a linear algebra course, it might be useful to mention which book you used and how many chapters you covered. This also applies to other advanced topics. An applicant might say they are proficient in cohomologies after half-listening to one half-hour lecture on the topic. This is not proficiency; it only indicates interest. If you claim advanced knowledge, specify the scope. The best way to start is by listing the books you have attempted to read. For each book, describe which chapters you only scanned, which chapters you read and understood, and for which chapters you solved all of the exercises.

Add more information if your first choice is number theory. Almost every year, we have several students requesting number theory. This might be explained by the successes of the Ross and PROMYS summer programs. The graduates from these programs love number theory and have a good number theory background. However, modern number theory is very advanced, and we seldom have these types of projects. So, if number theory is your top choice, there are two things you can do. First, mention your second choice. Second, specify what you like about number theory. For example, if you are into the more abstract parts of number theory, another abstract project might be a good fit.

Describe your priorities in broader terms. It is beneficial for every starting mathematician to figure out the area they like by asking themselves broader questions. If you know the answers to the questions below, it is helpful to write them on the application form.

• Do you love or hate abstractions?
• Do you prefer discreet or continuous problems?
• Is the real-life impact or inner beauty of your project more important to you?
• Do you enjoy having a visual component to your project?
• Do you like when problems involve programs and calculations?

If you follow my advice, you might get a project that matches your tastes better. Not only that: figuring out the answers to these questions will help you build the life you love.

I want to discuss a problem from a test I gave recently.

Problem. My dog, Fudge, likes books. He brought two books to his corner in the morning and three more books in the evening. How many books will he read tonight?

As I expected, many students didn’t pay attention and just summed up the two numbers in the problem and gave five as the answer. Here are three answers that I especially liked.

Answer 1. Zero, because most dogs can’t read.

This cautious student added most to be on the safe side.

Answer 2. You cannot tell how many books he will read. Just because he brings books to his corner doesn’t mean he will read them.

The second answer demonstrates great logical thinking, were Fudge a human. But the third answer made me laugh.

Answer 3. Three. If he brought three more books to his corner in the evening, it means he finished the two from that morning, so there are three books left for him to read.

I wrote a lot about how during entrance tests for Moscow State University, the examiners were giving Jewish and other undesirable students special (e.g. more difficult) questions during the oral exams. (See, for example, our paper Jewish Problems with Alexey Radul.) Not all examiners agreed to do this. So the administration made sure that there were different exam rooms: brutal rooms with compliant examiners torturing students with difficult questions, and normal rooms with normal examiners testing preapproved students. The administration also had other methods. One of them is the topic of this essay.

The math department of Moscow State University had four entrance exams. The first was a written math test consisting of three trivial problems, a very difficult one, and a brutally challenging one. At the end, I will show you a sample: a trivial problem and a very difficult one from 1976, my entrance year.

What was the point of such vast variation in difficulty, you may ask? There were two reasons.

But first, let me explain some entrance rules. The exam was scored according to the number of solved problems. A score of two or less was a failing score. People with such scores would be disqualified from the next exam. Any applicant with a smidge of mathematical intelligence would be able to solve all three trivial problems. Almost all applicants who qualified for the next test would have the same score of three on the first test, as they wouldn’t be able to solve the last two problems. Thus, mathematical geniuses and people who barely made the cut got the same score.

There was another rule. Officially, people with a gold medal from their high school (roughly equivalent to a valedictorian) could be accepted immediately if they scored 5 on the first exam. So one of the administrative goals was to prevent anyone getting a 5, thus, blocking Jewish applicants from sneaking in after the first exam.

Another goal was to have all vaguely qualified people get the same score. The same goal applied to other exams. After the four admission exams, the passing score, say X, was announced. A few people with a score higher than X were immediately accepted. Then there were hundreds of applicants with a score of X, way more than the quota of people the department was planning to accept. An official rule allowed the math department to pick and choose whoever they wanted from everyone who scored X.

I heard a speech by the famous Russian mathematician, Vladimir Arnold, directed at decent examiners who tested “approved” students at the oral math exam, which was the second admissions exam. His suggestion was brilliant and simple. If the students are good and belong in the department, give them an excellent grade of 5. If not, give them a failing grade of 2. Arnold’s plan boosted the chances of good students doing better than the cutoff passing score X and removed mediocre students from the competition. His idea was not only brilliant and simple but also courageous: he was risking his career by trying to fight the system.

I never experienced the entrance exams firsthand. By ministry order, as a member of the USSR IMO team, I was accepted without taking any exams. I already wrote an essay, A Hole for Jews, about how getting on the IMO team was the only way for Jewish students to get into the Moscow State University, and how the University tried to block them.

But I still looked at the entrance exam problems I would have had to solve to get in. The last two problems scared me. Now I found them again online (in Russian) at: the 1976 entrance test. The trivial problem below is standard and mechanical, while the other problem still looks scary.

Trivial problem. Solve for x:

Solution. We were drilled in school to solve these types of problems, so this one was trivial. First, make a substitution: y = 3^x. This leads to an equation: (2y – 1)(y – 3)/(y² – 2)(y – 1) ≤ 0. From this we get ranges for y: (-∞, -√2], [1/2,1], [√2, 3]. The last step is to take a logarithm.

Very difficult problem. Three spheres are tangent to plane P and to each other. Two of the spheres are the same size. The apex of a circular cone is on P, and the cone’s axis is perpendicular to the plane P. All three spheres are outside the cone and tangent to it. Find the cosine of the angle between the cone’s generatrix and the plane P, if one of the angles of the triangle formed by the intersection points of the spheres and the cone is 150 degrees.

I stumbled upon one of Smullyan’s puzzle on Facebook, in Russian. I couldn’t find the original text, so I just translated it back for my students.

Puzzle. You are on an island where only truth-tellers and liars live. The truth-tellers always tell the truth, and the liars always lie. You meet an islander who sits with you for a long time, then says, “I already said this sentence.” Is he a truth-teller or a liar?

I expected the following solution. If this islander is a truth-teller, then there should have been a time when he said, for the first time, “I already said this sentence.” But this would create a contradiction.

However, my students used this puzzle as an opportunity to teach me some intricacies of the English language. They explained to me the ambiguities of my translation. Here is a shortened and lightly edited quote from one of them:

There are two different linguistic opinions that give different answers to this problem. The first is that the truth of a statement is decided at the moment it starts to be delivered: in this case, when the islander starts saying his statement. With this interpretation, for the statement to be true, he had to have said the sentence before, and for that to be true, he had to have said it even before that, and this continues indefinitely. Clearly, he cannot have been alive forever, so he has to be a liar.
The other opinion is that the verity of a statement is decided at the exact conclusion of its deliverance. Then, when the islander finishes saying his sentence, its truth is judged, and he has at that same instant “already” said the sentence, so he is telling the truth. By this interpretation, the islander is a truth-teller.

Another student had a different brilliant idea. Depending on the islander’s intonation, it is possible that he says, “I already said ‘this sentence’.” In that case, there are no self-referencing sentences, and the islander could be either a truth-teller or a liar.

I consulted my best English consultant: my son, Alexey, and here is his reply. “The basic answer is that neither truth nor semantic meaning are absolute, and edge cases will be judged differently by different observers. A sentence whose truth is time-dependent on the same scale as the duration of uttering the sentence is clearly an edge case. That’s why mathematicians intentionally try to eliminate ambiguity from their communication.”

He suggested the following fix for the puzzle’s translation.

Fixed puzzle. You meet an islander who says, “I have said this sentence before.” Is he a truth-teller or a liar?

Alexey didn’t stop at fixes and suggested the following bonus puzzles.

Bonus puzzle 1. You meet an islander who says, “I will have said this sentence.” Is he a truth-teller or a liar?

Bonus puzzle 2. You meet an islander who says, “I will say this sentence again.” Is he a truth-teller or a liar?

Last year, our junior PRIMES STEP group studied Latin squares. We invented a lot of different types of Latin squares and wrote a paper about it, Fun with Latin Squares. Recall that a Latin square is an n by n table containing numbers 1 through n in every cell, so that every number occurs once in each row and column. In this post, I want to talk about anti-chiece Latin squares.

First, what’s a chiece? A chiece is a portmanteau word made out of two words, chess and piece, and, not surprisingly, it means a chess piece. Given a chiece, an anti-chiece Latin square is a Latin square such that any two cells, where our chiece can move from one cell to the other, according to the rules of chess, can’t contain the same number. Let’s see what this means.

Let’s start with rooks, which move along rows and columns. An anti-rook Latin square can’t have the same numbers repeating in any one row or column. Ha, anti-rook Latin squares are just Latin squares. Anti-bishop and anti-queen Latin squares can’t have the same numbers repeating on any diagonal.

Now, here is a picture of an anti-knight Latin square in which no two identical numbers are a knight’s move apart. This particular Latin square also forms a mini-Sudoku: not only does each row and column, but also each 2 by 2 corner region, contains all distinct numbers.

Consider all instances of some number, say 1, in an anti-chiece Latin square. If the board is n by n, we get n instances of non-attacking chieces. A famous math puzzle asks to place eight non-attacking queens on a standard chessboard. So the instances of any one particular number in an anti-queen Latin square solves the problem of placing n non-attacking queens on an n by n chessboard. Thus, building an anti-queen Latin square is more complicated than solving the non-attacking queens puzzle. The former requires filling the chessboard with n non-overlapping sets of non-attacking queens. The picture below gives an example of an anti-queen 5 by 5 Latin square.

This square has some interesting properties. It can be formed by cycling the first row. It also happens to be one of the chiece Latin squares we study in our paper. A chiece Latin square is a Latin square such that for each number in a cell, there is another cell, a chiece’s move apart, containing the same number. You can check that our anti-queen Latin square is at the same time a knight Latin square.

I wonder, can anyone build an anti-queen Latin square on the standard 8 by 8 chessboard?