Archive for the ‘Math Education’ Category.
Zipper Math

Each time I teach my students about the Möbius strip, I bring paper, scissors, and tape to class. The students make Möbius strips, and then I ask them to cut the strips in half along the midline and predict the result.
Then we move to advanced strips. To glue the Möbius strip, you need one turn of the paper. An interesting experiment is to glue strips with two, three, or more turns. In this case, too, it is fun to cut them along the midline and predict the shape of the resulting thingy. My class ends with a big paper mess.
As you might know, I am passionate about recycling. So I have always wanted to buy Möbius strips that can be cut in half and then put back together. I didn’t find them, so I made them myself from zippers. Now I can unzip them along the midline and zip them back together. I hope to have less mess in my future classes. We’ll see.
Share:Borromean Rings

Here are my newly-made Borromean rings: two identical sets of them. They are an example of three linked rings, with any two of them not linked. The top set is positioned the way the Borromean rings are usually presented. You can see that any two rings are not linked by mentally ignoring the third one. For example, the red ring is on top of the green one, the green one is on top of the blue one, and the blue one is on top of the red one. They have a non-transitive ordering.
The bottom set of rings is arranged for a lazier thinker. Obviously, the blue and green rings are not linked.
Share:
My Moscow State University Transcripts
I used to be proud of my Russian math education. I am still proud of my high school one, but not so much of the one I received in college. In Soviet Russia, a student had to choose their major before applying to college. I wanted to study mathematics, and I got accepted to the best place for it in Soviet Russia: mekhmat — the math school at the Moscow State University. I used to be proud of my education there, but now I have my doubts.
I had to take, on average, four math classes per semester for five years, which totals about 40 math classes. Woo hoo! I don’t think American students could even choose to take that many. This was presumably good, but most of the courses were required, and their curriculum remained unchanged for many, many years. Obviously, the system was very rigid. The faculty members feared retaliation from the communist party and forgot how to take initiative. The bureaucracy prevented the department from adding new and exciting math to the outdated curriculum.
This post is not about my grades but about the actual subjects that we were taught then. But, in case anyone is wondering, my only B was in English; everything else was straight As.
Some of the classes listed below lasted two or more semesters, that’s why they do not sum up to the promised 40. Unfortunately, I do not remember which ones. These were the required math classes:
- Analysis
- Analytical Geometry
- Advanced Algebra
- Theoretical Mechanics
- Linear Algebra and Geometry
- Differential Equations
- Partial Differential Equations
- Functions of Complex Variables
- Probability and Statistics
- Differential Geometry and Topology
- Numerical Methods
- Introduction to Mathematical Logic
- Control Theory
- Analysis III
- Computer Science and Programming
- Programming Practice
- Physics
- History and Methodology of Mathematics
- Thesis Work
An impressive list? But guess what — I remember nothing from most of these classes. As an exception, I remember bits of Differential Equations, taught by Vladimir Arnold, a charismatic teacher. I remember Linear Algebra well, not because of my Linear Algebra class, but because I read Gelfand’s book on the subject and loved it. I remember that the Differential Geometry and Topology class was taught by Fomenko with great pictures and boring material. By the time I took Fomenko’s class, I already knew topology from an unofficial class taught by Dmitry Fuchs, which was so much better. In fact, in order to learn what I wanted, I had to take many classes unofficially, so my total is actually way above 40.
By junior year, we were finally allowed to choose some classes which would count towards our transcripts, and this is what I picked.
- Infinite-Dimensional Representations of Lie Groups
- Theory of Functions of Many Complex Variables
- Representations of Lie Groups
- Discrete Mathematics
I remember these classes much more vividly. I also wrote a graduate thesis: “Models of Representations of Generalized Clifford Algebras.” I loved working on that paper.
We had non-math classes too: everyone had to take them.
- History of the Communist Party of the USSR
- Philosophy of Marxism-Leninism
- Political Economy
- Scientific Communism
- Foundations of Scientific Atheism
- Soviet Law
- Foreign Language (English)
- Physical Education
- Foundations of Marx-Lenin’s Aesthetics
To graduate, everyone had to pass two state exams: Mathematics and Scientific Communism. Whatever the latter might mean.
Did I mention that I am no longer proud of my former Soviet college education? What a colossal waste of time!
Share:
Hats and Time
Here is a classical puzzle I often give to my students.
Puzzle. The sultan has three red hats and two blue ones. He wants to test his three wizards, who know his hat collection. He asks them to close their eyes and puts a hat on each of their heads. After the wizards open their eyes, they see each other’s hats, but not their own. The sultan asks each of them to guess the color of their own hat, without communicating with each other. In this particular test, the sultan only puts red hats on the wizards’ heads. Sometime after the wizards open their eyes, one of them guesses his hat’s color. How did he guess?
Here is how my students explain the solution. If a wizard sees two blue hats, he immediately knows that his hat must be red. That means, if no one immediately announces their hat’s color, at least two of them are wearing red hats. In this case, if a wizard sees one red hat, he knows that his hat must also be red. So such a wizard can guess the color of his hat. If after some more time, no one announces their hat color, all the hats worn must be red.
After the students solve the problem, I run an evil experiment on them. I show the students my two blue and three red hats and ask three volunteers to close their eyes. Then, I put two red hats and one blue hat on their heads, and the blue hat goes on the fastest thinker in the group. I did this experiment many times. Half the time, the fastest thinker overestimates how fast the other students think and guesses, mistakenly, that s/he is wearing the red hat. Gotcha!
After the experiment, we discuss what is really going on in this puzzle. This is how I start my class on common knowledge.
Share:Preparing for My Knot Theory Class

I plan to teach knot theory to my students. So, I made four blue knots which are actually the four simplest non-trivial knots. Then I made the red ones which are mirror images of the blue ones.
Then I fiddled with the figure-eight knots, which are the second ones from the left. Out of all these four types of knots, the figure-eight knot is the only one that is amphichiral: its mirror image is equivalent to itself. It was fun to physically transform the red one to look identical to the blue one. So, I decided to crochet another pair of figure-eight knots for my students to fiddle with.
Did I mention that I hate crocheting?
Share:
Snowball Sentences
Here are some snowball sentences suggested by my students.
- I do not know about radon’s, osmium’s, polonium’s abilities.
- I am the only short person playing football.
- “I am not even smart,” mother remarks.
- I do not know where people acquire insanity.
- “A no,” Joe said while eating burgers mightily adultlike.
- I am not very happy during Mondays.
- I do not joke.
- I be—arr, mate—avast!
- I do not know super skates.
- I do not fear yucky cheese; however, kamikaze elephants jackhammer lumberjacks blackjacking backpedalling brontosauruses, artificializing territorializing icositetrahedrons.
Can you invent some other snowball sentences? But first, you need to figure out what they are.
Share:Clock Hands
Here is a cute old problem that Facebook recently reminded me of.
Puzzle. By mistake, a clock-maker made the hour hand and the minute hand on a clock exactly the same. How many times a day, you can’t tell the current time by looking at the clock? (It is implied that the hands move continuously, and you can pinpoint their exact location. Also, you are not allowed to watch how the hands move.)
Here is the solution by my son who was working on it together with my grandson.
The right way to think about it is to imagine a “shadow minute hand”, like this: Start at noon. As the true hour hand advances, the minute hand advances 12 times faster. If the true minute hand were the hour hand, there would have to be a minute hand somewhere; call that position the shadow minute hand. The shadow minute hand advances 12 times faster than the true minute hand. The situations that are potentially ambiguous are the ones where the shadow minute hand coincides with the hour hand. Since the former makes 144 circuits while the latter makes 1, they coincide 143 times. However, of those, 11 are positions where the true minute hand is also in the same place, so you can still tell the time after all. So there are 132 times where the time is ambiguous during the 12-hour period, which leads to the answer: 268.
I love the problem and gave it to my students; but, accidentally, I used CAN instead of CAN’T:
Puzzle. By mistake, a clock-maker made the hour hand and the minute hand on a clock exactly the same. How many times a day can you tell the current time by looking at the clock?
Obviously, the answer is infinitely many times. However, almost all of the students submitted the same wrong finite answer. Can you guess what it was? And can you explain to me why?
Share:My Virtual Stars
I like rewarding my students. Before covid, I used to give them star stickers for good ideas. When I started to teach remotely, I wondered what I should do instead. I could tell them that they had won a star, but it felt too weak. The next idea was to show them a star and tell them that it belonged to them. But that still felt insufficient. Then I had an epiphany. I would say to them they earned a star, show it to them, and stick it to my face. So they, and all the other students, would see it for the rest of the class. The photo shows how I looked at the end of a successful lesson.

Another picture shows what my MathRoots students posted on our Discord channel.
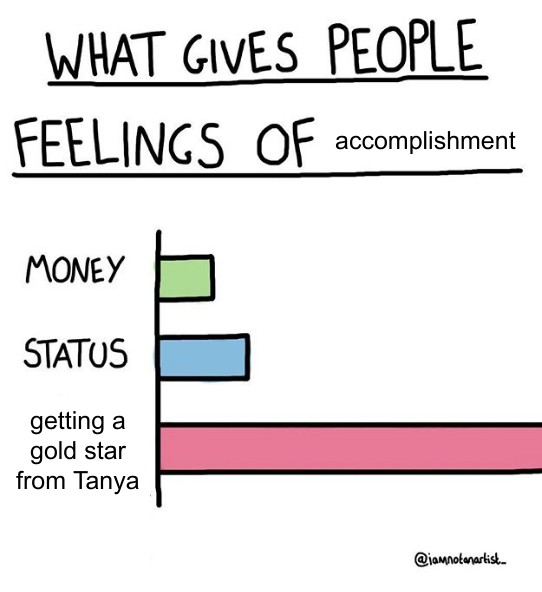
Now that I am back teaching in person, my students asked me to continue sticking their stars to my face. Sometimes I forget about the stars and, after my class, wander around MIT star-covered.
Share:
Joint-Groups Sudoku
My students (Matvey Borodin, Eric Chen, Aidan Duncan, Boyan Litchev, Jiahe Liu, Veronika Moroz, Matthew Qian, Rohith Raghavan, Garima Rastogi, Michael Voigt) and I recently wrote a paper connecting the stable marriage problem and Sudoku. I just blogged about it. By the way, my students are in grades 7-9.
On the way, we invented a new type of Sudoku, which we call joint-groups Sudoku. This type is in contrast to a famous type of Sudoku, called disjoint-groups Sudoku. In a disjoint-groups Sudoku, in a particular place in a 3 by 3 box, all the digits are distinct across all the boxes. For example, the top-left corners of nine boxes have all the digits 1 thought 9. This creates nine additional disconnected regions (depending on the placements inside a 3 by 3 box) to add to columns, rows, and boxes that have to contain distinct digits.
For our new type, we wanted the digits in a particular place in each box, instead of being different, to be the same as much as possible. How much of sameness is possible? The first row contains three top-left corners. Thus, by Sudoku rules, these top-left corners have to be distinct. Thus, the top-left corners in all nine boxes have to contain at least three distinct digits. So here is the rule for the joint-groups Sudoku: the nine digits in a particular place in a 3 by 3 box contain not more than three distinct digits. It is easy to see that it means they contain exactly 3 distinct digits, each of them three times.
Here are two Sudoku puzzles from our paper. Each puzzle, when completed, forms a joint-groups Sudoku.
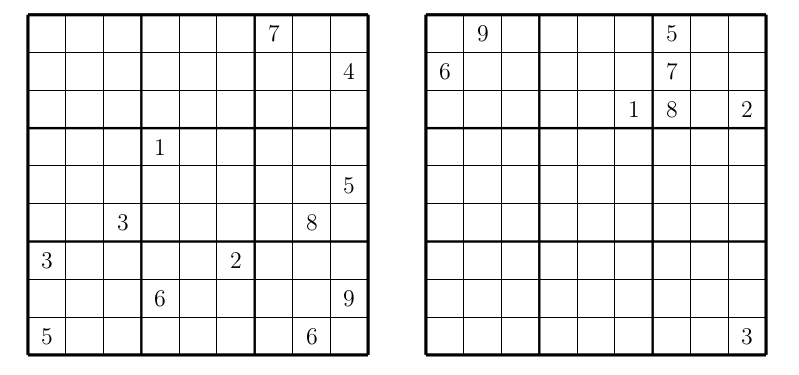
Share:
