Thinking Inside and Outside the Box
The most famous thinking-outside-the-box puzzle is the Nine-Dots puzzle. This puzzle probably started the expression, “To think outside the box”. Here is the puzzle.
Puzzle. Without lifting the pencil off the paper, connect the nine dots by drawing four straight continuous lines that pass through all the dots.

Most people attempt something similar to the picture below and fail to connect all the dots.
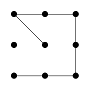
They try to connect the dots with line segments that fit inside the square box around the dots, mentally restricting themselves to solutions that are literally inside the box.
To get to the correct solution, the line segments should be drawn outside this imaginary box.
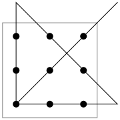
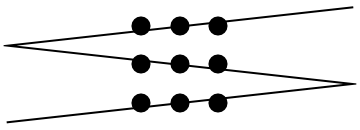
Do you think that four line segments is the best you can do? Jason Rosenhouse showed me a solution for this puzzle that requires only three lines. Here, the outside-the-box idea is to use the thickness of the dots.
This and many other examples of thinking outside the box are included in my paper aptly titled Thinking Inside and Outside the Box and published in the G4G12 Exchange book.
A section of this paper is devoted to my students, who sometimes give unexpected and inventive solutions to famous puzzles. Here is an example of such a puzzle and such solutions that aren’t in the paper because I collected them after the paper was published.
Puzzle. Three men were in a boat. It capsized, but only two got their hair wet. Why?
The standard answer is the following: One man was bald.
Lucky for me, my creative students suggested tons of other solutions. For example,
- One man was wearing a waterproof helmet.
- The boat capsized on land, and two men had their hair already wet.
My favorite example, however, is the following.
- One man didn’t have a head.
Share:
JBL:
Jason Rosenhouse’s solution to the nine dots problem is related to what I call in class the Big Point Theorem: any three lines are concurrent, provided you draw the point large enough.
31 July 2022, 1:31 pmtanyakh:
JBL, You made me laugh. I love your Big Point Theorem.
31 July 2022, 1:40 pmIvan:
The third man was Newton and he was standing on the shoulders of the others.
2 August 2022, 3:01 pmGeorge R.:
Ivan’s Newton is a fantastic answer! 👍
3 August 2022, 9:48 amThe third man could also -very trivially- of course be Jesus…
Tanya Khovanova's Math Blog » Blog Archive » Another Nine-Dots Puzzle:
[…] recently wrote an essay, Thinking Inside and Outside the Box, which starts with a famous nine-dots puzzle that kicked off the expression: thinking outside the […]
5 August 2022, 5:27 pmJBL:
Thanks :). I have a strong feeling that there should also be a dual theorem of the form
every three points are collinear, provided you draw the line [blank] enough
but I’ve never been quite satisfied with my choices for filling in the blank; suggestions welcome.
5 August 2022, 9:12 pmtanyakh:
JBL, wide enogh? Continuing with this reasoning, any three points are the same point.
7 August 2022, 10:12 amLeo B.:
Why do people keep implying that the only place humans have hair is the head? The standard answer should be “one person had total alopecia”.
11 August 2022, 2:40 pmJBL:
“wide” is definitely better than “wiggly” or “curvy”, which is what I’ve used before.
13 August 2022, 7:40 pmTanya Khovanova's Math Blog » Blog Archive » The Big Point Theorem:
[…] to the subject matter. Joel Lewis made a comment on my recent post, thinking-outside-the-box ideas. He mentioned his two […]
16 August 2022, 10:24 amChris:
If you think really far outside the box, you could do the nine-dots puzzle with only one line.
The catch is, you have to be on a round body (like a planet) on which you can circle (circumnavigate?) the body while drawing the line.
The line has to be angled from horizontal (or vertical) a tiny amount so that on the subsequent passes through the dot matrix, the line will pass through the next set of dots. Each subsequent pass takes place after a full circumnavigation of the round body you’re on. All while continuously drawing the line.
Easiest to do on a small round asteroid a few meters across. Provided you can get there. 🙂
9 September 2022, 3:18 amTanya Khovanova's Math Blog » Blog Archive » The Big Point Theorem - New Marathi Live:
[…] to the subject matter. Joel Lewis made a comment on my recent post, thinking-outside-the-box ideas. He mentioned his two […]
16 September 2022, 7:07 am