Fun with Latin Squares
Last year, our junior PRIMES STEP group studied Latin squares. We invented a lot of different types of Latin squares and wrote a paper about it, Fun with Latin Squares. Recall that a Latin square is an n by n table containing numbers 1 through n in every cell, so that every number occurs once in each row and column. In this post, I want to talk about anti-chiece Latin squares.
First, what’s a chiece? A chiece is a portmanteau word made out of two words, chess and piece, and, not surprisingly, it means a chess piece. Given a chiece, an anti-chiece Latin square is a Latin square such that any two cells, where our chiece can move from one cell to the other, according to the rules of chess, can’t contain the same number. Let’s see what this means.
Let’s start with rooks, which move along rows and columns. An anti-rook Latin square can’t have the same numbers repeating in any one row or column. Ha, anti-rook Latin squares are just Latin squares. Anti-bishop and anti-queen Latin squares can’t have the same numbers repeating on any diagonal.
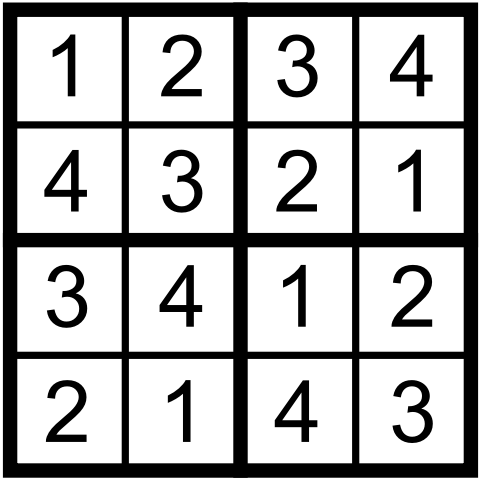
Now, here is a picture of an anti-knight Latin square in which no two identical numbers are a knight’s move apart. This particular Latin square also forms a mini-Sudoku: not only does each row and column, but also each 2 by 2 corner region, contains all distinct numbers.
Consider all instances of some number, say 1, in an anti-chiece Latin square. If the board is n by n, we get n instances of non-attacking chieces. A famous math puzzle asks to place eight non-attacking queens on a standard chessboard. So the instances of any one particular number in an anti-queen Latin square solves the problem of placing n non-attacking queens on an n by n chessboard. Thus, building an anti-queen Latin square is more complicated than solving the non-attacking queens puzzle. The former requires filling the chessboard with n non-overlapping sets of non-attacking queens. The picture below gives an example of an anti-queen 5 by 5 Latin square.

This square has some interesting properties. It can be formed by cycling the first row. It also happens to be one of the chiece Latin squares we study in our paper. A chiece Latin square is a Latin square such that for each number in a cell, there is another cell, a chiece’s move apart, containing the same number. You can check that our anti-queen Latin square is at the same time a knight Latin square.
I wonder, can anyone build an anti-queen Latin square on the standard 8 by 8 chessboard?
Share:
CharlesG:
Thank you for this. I really enjoy Latin Squares and am always looking for creative ways to play with them and puzzles to code up for them. The cross between Latin Squares and chess is one I hadn’t heard of before so thanks for that. I’m reading through the paper right now. Thanks!
25 March 2022, 8:37 amJBL:
So the answer to the final question is “no” but I wonder if you know a good reason they don’t exist (rather than just taking advantage of the fact that 92 is rather small and checking on a computer, as I did).
1 April 2022, 7:55 pmtanyakh:
JBL, no I do not have a good reason. I didn’t even have a proof, just a gut feeling.
1 April 2022, 9:54 pmCharlesG:
I’m back and full of questions. I’m not sure if you’ll have time to get to them but I’ll leave them here anyway as a reference. What got me into Latin Squares are Sudoku puzzles. One famous open (at least then it was open) was the minimum number of cells that were necessary to still have a unique Sudoku puzzle. When I read up on this years ago, the number was somewhere around 17 or 18 but I think most “challenging” puzzles left somewhere between 25-30 clues.
I ask this because I like to generate puzzles (https://learninglover.com/puzzles/) and when I read your post I was in the middle of creating a puzzle on Latin Squares. Initially I was going to play with your results as different types of puzzles to try (Basic/Knights/Bishop/King) but reading your paper and seeing difficulty that my puzzle generation algorithm is having with producing the Bishop and King Latin Squares, I may refrain from doing this,
But back to my question. In your paper you mention things like the existence of these Latin Squares of different types. Have you given any thought into the minimum representation of them? For example for the grid,
12345
34512
51234
23451
45123
we have a representation
__3__
3___2
__2__
_3___
4_1_3
revealing 8
_2___
___12
5_2__
____1
4_12_
revealing 9
_2___
___1_
__2__
_3___
4___1
revealing 6
Have you given any thought into this problem or has any work been done on the general minimum representation of Latin Squares and these new classes of Latin Squares in particular?
Ok, I don’t want to ramble any more but I had to get this idea out of my head.
2 April 2022, 10:24 pmtanyakh:
CharlesG, we dind’t think about the minimum number of clues. BTW, this number is 17 for Sudoku.
6 April 2022, 12:21 pmLatin Squares are so Beautiful | LEARNINGlover.com:
[…] was recently reading another math blog on Latin Squares and it brought the concept back to the forefront of my mind. For years I have […]
6 April 2022, 5:48 pmPlayful Math Carnival #154: The Math Journaling Edition – Denise Gaskins' Let's Play Math:
[…] Tanya Khovanova shares a puzzle from the Kyiv Olympiad, 1978. Also, check out her post about Anti-Chiece Latin Squares. […]
28 April 2024, 12:57 pm