Marriage Proposals, Or How I Learned to Say No
In the name of privacy, I have changed the names of the men I did not marry. But there is no point in changing the names of my ex-husbands, as my readers probably know their names anyway.
I received my first marriage proposal when I was 16. As a person who was unable to say “no” to anything, I accepted it. Luckily, we were not allowed to get married until I was 18, the legal marriage age in the USSR, and by that time we broke up.
To my next proposal, from Sasha, I still couldn’t say “no”, and ended up marrying him. The fact that I was hoping to divorce him before I got married at 19 shows that I should have devoted more effort in learning to say “no”. I decided to divorce him within the first year.
My next proposal came from Andrey, I said yes, with every intention of living with Andrey forever. We married when I was 22 and he divorced me when I was 29.
After I recovered from my second divorce, I had a fling with an old friend, Sam, who was visiting Moscow on his way to immigrate to Israel.
Sam proposed to me in a letter that was sent from the train he took from the USSR to Israel. At that point I realized I had a problem with saying “no”. The idea of marrying Sam seemed premature and very risky. I didn’t want to say yes. I should have said no, but Sam didn’t have a return address, so I didn’t say anything.
That same year I received a phone call from Joseph. Joseph was an old friend who lived in the US, and I hadn’t seen or heard from him for ten years. He invited me to visit him in the US and then proposed to me the day after my arrival. The idea of marrying Joseph seemed premature and very risky, but in my heart it felt absolutely right. I said yes, and I wanted to say yes.
I was very glad that I hadn’t promised anything to Sam. But I felt uncomfortable. So even before I called my mother to notify her of my marriage plans, I located Sam in Israel and called him to tell him that I had accepted a marriage proposal from Joseph. I needed to consent to marry someone else as a way of saying “no” to Sam.
After I married Joseph, I came back to Russia to do all the paperwork and pick up my son, Alexey for our move to the US. There I met Victor. I wasn’t flirting with Victor and was completely disinterested. So his proposal came as a total surprise. That was the time I realized that I had a monumental problem with saying “no”. I had to say “no” to Victor, but I couldn’t force myself to pronounce the word. Here is our dialogue as I remember it:
- Me: I can’t marry you, I am already married.
- Victor: I am sure it’s a fictitious marriage; you just want to move to the USA.
- Me: That’s not true. It’s a real marriage.
- Victor: If it were a fictitious marriage, you wouldn’t admit it. So, it’s a fictitious marriage. My proposal stands.
My sincere attempt at saying “no” didn’t work. I moved to the US to live with Joseph and I soon got pregnant. Victor was the first person on my list to notify — another rather roundabout way to reject a proposal.
The marriage lasted eight years. Sometime after I divorced Joseph, I met Evan who invited me on a couple of dates. I wasn’t sure I wanted to get involved with him. But he proposed and got my attention. I was single and available, though I had my doubts about him.
Evan mentioned that he had royal blood. So I decided to act like a princess. I gave him a puzzle:
I have two coins that together make 15 cents. One of them is not a nickel. What are my coins?
He didn’t solve it. In and of itself, that wouldn’t be a reason to reject a guy. But Evan didn’t even understand my explanation, despite the fact that he was a systems administrator. A systems administrator who doesn’t get logic is a definite turn-off.
So I said “no”! That was my first “no” and I have mathematics to thank.
Share: When the
When the  Sergei Bernstein and Nathan Benjamin brought back a variation of the
Sergei Bernstein and Nathan Benjamin brought back a variation of the 
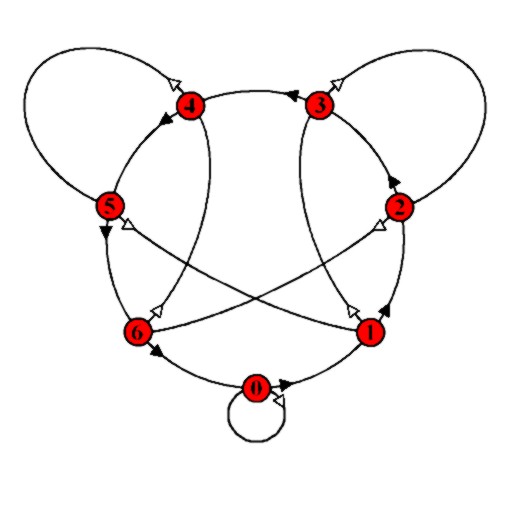 The graph is used in the same way as the first graph. To find the remainder on dividing a number by 7, start at node 0, for each digit D of the number, move along D black arrows (for digit 0 do not move at all), and as you pass from one digit to the next, move along a single white arrow.
The graph is used in the same way as the first graph. To find the remainder on dividing a number by 7, start at node 0, for each digit D of the number, move along D black arrows (for digit 0 do not move at all), and as you pass from one digit to the next, move along a single white arrow.