Conway’s Circle
John Conway has a T-shirt with his theorem on it. I couldn’t miss this picture opportunity and persuaded John to pose for pictures with his back to me. Here is the theorem:
If you continue the sides of a triangle beyond every vertex at the distances equaling to the length of the opposite side, the resulting six points lie on a circle, which is called Conway’s circle.
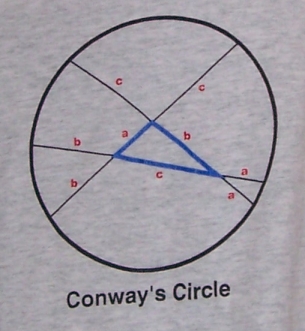
Poor John Conway had to stand with his back to me until I figured out the proof of the theorem and realized which point must be the center of Conway’s circle.
misha:
Lol, poor John, I hope you figured it out fast enough, so he didn’t suffer too much.
13 June 2010, 8:19 amJBL:
Now, did you figure out that the perpendicular bisector of the segment joining the endpoints of the two extensions through vertex A is also the angle bisector of angle A (my first solution), or via the more natural observation that the three chords have the same length and so any center must be equidistant from them (which seems like an optimally fast way to figure out what the center is, though I don’t see how to translate it as easily into a proof that the six points are actually concyclic), or some other way?
13 June 2010, 8:14 pmTanya Khovanova:
JBL,
I did your first solution. From your observation it follows that the in-centre is at the same distance from any two consecutive points on the circle.
29 June 2010, 11:41 amC y N:
Hello we are Carol and Natalia Montecinos Sepulveda, Catholic University of Maule, Chile and we very interested in your blog, but if we stay the doubt of the center point of the circle to guide us more about where they stood exactly the triangle as straight lines projecting from the sides of the triangles are of equal measure to his side. And knowing we can build it and really check it and to work with this formula in our homework and study the race as pedagogy in mathematics. Ojala interesting follow up work like this and the other to go practice and learn more.
28 July 2010, 11:36 pmCharles Worrall:
Here’s a fun theorem I’ve proved recently. I didn’t know it was connected to John Conway!
Theorem: Consider the midpoint F of the arc AB on the circumcircle of triangle ABC. There is a unique parabola with focus F that is tangent to all three sides of ABC; furthermore the parabola’s tangent points on sides AC and BC are two of the six points on the Conway Circle.
I’ve got an aesthetically pleasing proof using some of Archimedes’ theorems about parabolas…
15 February 2012, 2:18 pmTom Shannon:
I’d like to add a couple of corollaries to John Horton Conway’s Circle Theorem.
1. The radius of the Conway Circle equals the sum of the triangle’s side lengths divided by two.
CC r = a+b+c over 2
2. In the case of the equilateral triangle the radius of the Conway Circle is 5 times the radius of the triangle’s incircle .
Respectfully,
2 June 2020, 1:53 pmTom Shannon
June 2, 2020
La circunferencia de Conway - Gaussianos:
[…] ¿Y quién mejor para hacerlo que el propio John Horton Conway? Pues ahí la tenéis, tomada de este post del blog de Tanya Khovanova (lugar por el que supe por primera vez sobre la existencia de este […]
10 July 2023, 5:48 pmFrancisco Javier García Capitán:
Do you know when Conway discovered his theorem?
18 October 2023, 1:29 amtanyakh:
Fransisco, I do not know then Conway discovered the theorem.
18 October 2023, 12:12 pmYi Zhang:
Can you let wikipedia know that their radius of the Conway circle is wrong. https://en.m.wikipedia.org/wiki/Conway_circle_theorem#:~:text=In%20plane%20geometry%2C%20the%20Conway,the%20incentre%20of%20the%20triangle.
25 August 2024, 1:02 pmIt’s ‘a+b+c’ instead of ‘abc’
tanyakh:
Thank you, Yi. Done.
25 August 2024, 1:41 pmYi Zhang:
Thank you so much for your prompt reply and correction. Toda Raba!
26 August 2024, 11:29 am