We worked for several years with RSI where we supervised summer math research projects by high school students. Now, we’ve started an additional program at MIT’s math department called PRIMES, where local high school students do math research during the academic year. In this essay we would like to discuss what makes a good math research project for a high school student.
A doable project. The project should not be believed to be extremely difficult to yield at least results. It is very discouraging for an aspiring mathematician not to produce anything during their first project.
An accessible beginning. The student should be able to start doing something original soon after the start of the project. After all, they don’t come to us for coursework, but for research.
Flexibility. It is extremely important to offer them a project that is adjustable; it should go in many directions with many different potential kinds of results. Since we do not know the strength of incoming students in advance, it is useful to have in mind both easier and harder versions of the project.
Motivation. It is important for the project to be well motivated, which means related to other things that have been studied and known to be interesting, to research of other people, etc. Students get more excited when they see that other people are excited about their results.
A computer component. This is not a must for a good project. But modern mathematics involves a lot of computation and young students are better at it than many older professors. Such a project gives young students the opportunity to tackle something more senior people are interested in but might not have enough computer skills to solve. In addition, through computer experiments students get exposed to abstract notions (groups, rings, Lie algebras, representations, etc.) in a more “hands-on” way than when taking standard courses, and as a result are less scared of them.
A learning component. It is always good when a project exposes students to more advanced notions.
The student should like their project. This is very difficult to accomplish when projects are chosen in advance before we meet the students. However, we try to match them to great projects by using the descriptions they give of their interests on their applications. It goes without saying that mentors should like their project too.
Having stated the desired properties of a good project, let us move on to giving examples: bad projects and good projects. We start with a bad one:
Prove that the largest power of 2 that doesn’t contain 0 is 286.
The project satisfies only one requirement: it contains a computer component. Otherwise, it doesn’t have an accessible beginning. It is not very flexible: if the student succeeds, the long-standing conjecture will be proven; if s/he doesn’t, there is not much value in intermediate results. The question is not very interesting. The only motivation is that it has been open for a long time. Also, there is not much to learn. Though, almost any theoretical question can be made flexible. We can start with the question above and change its direction to make it more promising and enticing.
Another bad example is a project where the research happens after the programs are written. This is bad because it is difficult to estimate the programming abilities of incoming students. It doesn’t have an accessible beginning and there is no flexibility until the programming part is finished. If the student can’t finish the programming quickly, s/he will not have time to look at the results and produce conjectures. For example, almost any project in studying social networks may fall into this category:
Study an acquaintance graph for some epic movies or fiction, for example Star Wars or The Lord of the Rings. In this graph people are vertices and two people are connected by an edge if they know each other. The project is to compare properties of such graphs to known properties of other social networks.
Though the networks in movies are much smaller than other networks that people study, the amount of programming might be substantial. This project can be a good project for a person with a flexible time frame or a person who is sure in advance that there will be enough time for him/her to look at the data.
Now on to an example of a good project. Lynnelle Ye and her mentor, Tirasan Khandhawit, chose to analyze the game of Chomp on graphs during RSI 2009.
Given a graph, on each turn a player can remove an edge or a vertex together with all adjacent edges. The player who doesn’t have a move loses. This game was previously solved for complete graphs and forest graphs, so the project was to analyze the game for other types of graphs.
It is clear how to analyze the game for any particular new graph. So that could be a starting point providing an accessible beginning. After that the next step could be to analyze other interesting sets of graphs. The flexibility is guaranteed by the fact that there are many sets of graphs that can be used. In addition, the project entails learning some graph theory and game theory. And the project has a computational component.
Lynnelle Ye successfully implemented this project and provided a complete analysis of complete n-partite graphs for arbitrary n and all bipartite graphs. She also gave partial results for odd-cycle pseudotrees. The paper is available at the arxiv. Not surprisingly, Lynelle got fourth place in the Intel Science Talent Search and second place in the Siemens Competition.
Share:





![]()
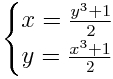
 I am reading the book
I am reading the book