World Championship Puzzles
 Do you like challenging puzzles? Are you tired of sudoku? Here’s your chance to try your hand at puzzles that are designed for world puzzle championships.
Do you like challenging puzzles? Are you tired of sudoku? Here’s your chance to try your hand at puzzles that are designed for world puzzle championships.
I’ve already done the homework for you — and it turned out to be more complicated than I anticipated. The world puzzle federation has a website, but unfortunately they are lazy or secretive. It is difficult to find puzzles there. A few puzzles are available in the World Puzzle Federation Newsletters.
Since I am stubborn, I spent a lot of time looking for championship puzzles. I found them in books. Here is the list I compiled so far. If you too are interested in high-level puzzles, this ought to make your search a lot easier. The book titles are confusing, so I added a description of what’s in them.
- Games Magazine Presents Brain Twisters from the First World Puzzle Championships — Warm-up puzzles, US/Canada Qualifying test, First World Championship, Foreign team puzzles.
- Games Magazine Presents Brain Twisters from the World Puzzle Championships, Volume 2 — US/Canada Qualifying test, Second World Puzzle Championship, Third World Puzzle Championship.
- Games Magazine Presents Brain Twisters from the World Puzzle Championships, Volume 3 — Fourth World Puzzle Championship, Fifth World Puzzle Championship.
- World Puzzle Championships Omnibus, Volume 1 — Contains World-Class Puzzles from the World Puzzle Championships Volumes 1-3 below.
- World-Class Puzzles from the World Puzzle Championships, Volume 1 — Sixth World Puzzle Championship and Seventh World Puzzle Championship.
- World-Class Puzzles from the World Puzzle Championships, Volume 2 — 1999 Qualifying test, Eighth World Puzzle Championship.
- The New York Times Sunday Crossword Omnibus, Volume 3 — 2000 Qualifying test, Ninth World Puzzle Championship.
- World-Class Puzzles from the World Puzzle Championships, Volume 4 — 2001 Qualifying test, Tenth World Puzzle Championship.
- World-Class Puzzles from the World Puzzle Championships, Volume 5 — 2002 Qualifying test, Eleventh World Puzzle Championship.
- Random House World-Class Puzzles — 2002 Qualifying test, Twelfth World Puzzle Championship. (The year for the qualifying test is probably a typo as puzzles differ from the qualifying test in the previous book,)
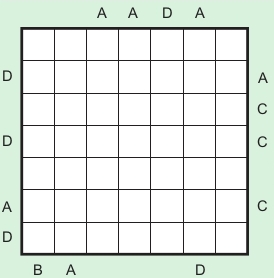
One of my favorite puzzle types is Easy as ABC. You have to fill one of A, B, C, and D in each row and column. The letters outside the grid indicate which letter you see first from that direction. Here is one from the 2011 newsletter:
 I have a problem with my binocular vision. The muscles that are responsible for moving my eyes outwards are very weak, much weaker than the muscles that move my eyes inwards. When I am very tired, I can’t focus on people or things that are far away. I start seeing doubled monsters with extra eyes and noses.
I have a problem with my binocular vision. The muscles that are responsible for moving my eyes outwards are very weak, much weaker than the muscles that move my eyes inwards. When I am very tired, I can’t focus on people or things that are far away. I start seeing doubled monsters with extra eyes and noses.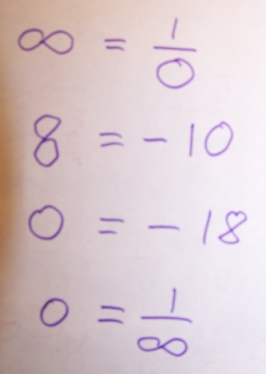 I found a strange piece of paper in an old pile. I believe that it is a visual proof of the following statement:
I found a strange piece of paper in an old pile. I believe that it is a visual proof of the following statement: