The Most Colorful Independent Set
Tanya Khovanova and Richard Stanley

On the left is a puzzle from the 2000 Qualifying Test for USA and Canada teams to compete in the world puzzle championship. A set of all 21 dominoes has been placed in a 7 by 6 rectangular tray. The layout is shown with the pips replaced by numbers and domino edges removed. Draw the edges of the dominoes into the diagram to show how they are positioned.
We would like to discuss the mathematical theory behind this puzzle using a toy example below. Only three dominoes: 1-1, 1-2, 2-2 are positioned on the board and the goal is to reconstruct the positioning:
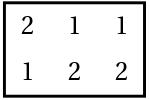
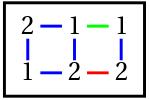
Let’s connect adjacent numbers with segments to show potential dominoes and color the segments according to which domino they represent. The 1-1 edge is colored green, the 1-2 — blue, and the 2-2 — red. Now our puzzle has become a graph, where the numbers are vertices, the segments are edges, and the edges are colored. In this new setting, the goal of the puzzle is to find edges of three different colors so that they do not share vertices.
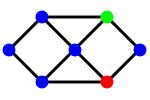
The next picture represents the line graph of the previous graph. Now the colors of the vertices correspond to different potential dominoes. Vertices are connected if the corresponding dominoes share a cell. In the new setting finding dominoes that do not share a cell is equivalent to finding an independent set. The fact that we need to use all possible dominoes means that we want the most colorful independent set.
JBL:
Hi Tanya and Richard,
Two observations:
14 December 2011, 4:10 pm1) If we seek independent sets with the maximum number of colors represented, then we never need to consider an independent set with two vertices of the same color: we can simply throw out duplicates.
2) Consequently, the problem of finding the independent set with maximum number of colors reduces to the problem of finding an independent set of maximum size on the following modification of your graph: after taking the line graph, draw extra edges connecting any pair of vertices of the same color. (An independent set on this graph is the same as an independent set on the line graph that contains no two vertices of the same color.)
Basil:
Interesting problem! This would be a great extension to a problem I do from the Connected Mathematics book “Clever Counting”. Students have one section in the book that pushes them toward graph theory, but it never is really developed in further. I think this would connect two of the investigations well.
29 December 2011, 6:52 pmMerlin:
Well, there are some footholds. The pair 5-5 is only in the upper right corner.
16 April 2012, 7:41 pmThen there are only two 4-4 pairs, and one of them must be correct.
You should follow both “4-4” paths consequently.
If e.g. the 4-4 on the left is right, then also the 2-4 pair in the upper left corner should be right, etcetera.
If there are any forced doubles left, then the followed path is wrong.
By means of making trees and elimination the answer should be found, but I am not going to write down all these numbers in tenfold…
Bert:
Very original problem that looks deceptively simple. One of the nice things is that anyone can write down a variant of this problem on the back of an envelope, which has at least one solution.
15 April 2018, 1:19 pmCreating a problem that has a unique solution (like the one above) is less obvious, or isn’t it ?