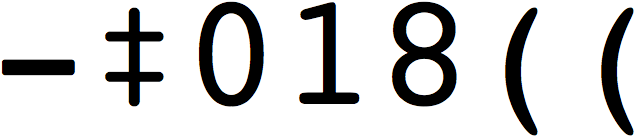Tanya Khovanova's Math Blog

Cambridge Waldo puzzle from the 2013 MIT Mystery Hunt was supposed to be easy. Its goal was to get people out of the building for some fresh air. I made this puzzle jointly with Ben Buchwald, Adam (Pesto) Hesterberg, Yuri Lin, Eric Mannes and Casey McNamara. The puzzle consists of 50 pictures of different locations in Cambridge; one of the above individuals was hiding in each picture. Let me use this opportunity to thank my friends for starring in my puzzle and being inventive while doing it.

The puzzle starts with a group picture of my stars. The caption to the picture gives their names. The fact that they are standing in alphabetical order is a clue.

Out of the 50 pictures, each person appears in exactly ten pictures. If you mark the locations of one person on a map, they look like a letter. For example, below are Ben’s locations that form a letter “S”. When you put the letters in the alphabetical order by people names you get the answer to the puzzle: SCAMP.

As you can see, you do not need all ten locations to recognize the letter. You might be able to recognize the letter with five locations, or at least significantly reduce possibilities for the letter. Besides, you do not need all the letters to recognize the answer. We thought that this was an easy puzzle.

And, to make it even easier, the order in which we posted the pictures was not completely random. The pictures of one person were in the order one might walk from one location to another. This played two important roles. If you recognize the person but do not recognize the location on the picture, you can make an approximate estimation of the location because it must be on the path between the previous and next locations. If you recognize the location but not the person, you can guess the person by checking whose path it fits better.

It was difficult to hide people, especially when there were no other people around. So we sometimes used props. We only used one prop per person. Here you can see Pesto with his sarongs in plain view. In the other picture (below) he is hiding under a white sarong. Yuri had a bicycle helmet. In one of the pictures, she hid so well that you couldn’t see her — but you could see her helmet. Ben had a bear hat. In one of the pictures you can only see a shadow of a person, but this person was clearly wearing a hat with bear ears. Eric didn’t have a prop, but my car was eager to make a cameo appearance at the Mystery Hunt, so I hid him in my car in one of the pictures.

As you might guess I made the pictures of different people at different times. So Ben Buchwald was the one who realized that solvers might differentiate people by looking at the data of the picture files. He carefully removed the original time stamps.

Despite our best intentions, our test-solvers decided not to leave their comfy chairs, but rather to use Google-StreetView. We strategically made some of the pictures not Google-StreetViewable, but our test-solvers still didn’t leave the comfort of their chairs. They just became more inventive. I do not know all the things they did to solve the puzzle, but I heard about the following methods:

• Finding a website with parking meter locations by meter number.
• Looking for one-way streets in the proper configuration to find likely places for One-Way/Do-Not-Enter signs.
• Looking up the street cleaning signs in the street cleaning schedule.
• Differentiating the streets by their separator line: double, single, or no line.

I have yet to understand why this puzzle was difficult for the Mystery Hunt teams.

Here is the solution to the Open Secrets puzzle I published recently. Through my discussion of this solution, you’ll also get some insight into how MIT Mystery Hunt puzzles are constructed in general.

I’ve included the puzzle (below) so that you can follow the solution. The puzzle looks like a bunch of different cipher texts. Even before we started constructing this puzzle, I could easily recognize the second, the seventh, and the last ciphers. The second is the cipher used by Edgar Allan Poe in his story, The Gold-Bug. The seventh cipher is a famous pigpen (Masonic) cipher, and the last is the dancing men cipher from a Sherlock Holmes story. Luckily you do not need to know all the ciphers to solve the puzzle. You can proceed with the ciphers you do know. With some googling and substitution you will translate these three pieces of text into: COLFERR, OAOSIS OF LIFEWATER, and RBOYAL ARCH.

These look like misspelled phrases, each of which has an extra letter. However, there are no typos in good puzzles. Or, more precisely, “typos” are important and often lead to the answer. So now I will retype the deciphered texts with the extra letter in bold: COLFERR, OAOSIS OF LIFEWATER and RBOYAL ARCH. In the first word it is not clear which R should be bold, but we will come back to that later.

At this point you should google the results. You may notice that the “royal arch” leads you to the Masons, who invented the pigpen cipher. From this, you can infer the structure of the ciphers and the connections among them. Indeed, a translation of one cipher refers to another. So you should proceed in trying to figure out what the texts you have already deciphered refer to. Eoin Colfer is the author of the Artemis Fowl series that contains a Gnomish cipher, and Oasis of Lifewater will lead you to Commander Keen video games with their own cipher. When you finish translating all of the ciphers, you get the following list:

• AQUAL MAGNA: in Coldplay’s X&Y Baudot code
• COLFERR: in Edgar Allen Poe’s “The Gold-Bug” cipher
• DOCTOR WEFRNSTROM: in Daedric from the Elder Scrolls series
• ELEMENTARHY: in Futurama’s Alienese
• MYLKO XYLOTO: in Commander Keen’s Standard Galactic Alphabet
• NEVEROMORE: in Bionicle’s Matoran alphabet
• OAOSIS OF LIFEWATER: in the Pigpen (Masonic) cipher
• ORANGE DYARTWING: in Eoin Colfer’s Gnommish from Artemis Fowl series
• RBOYAL ARCH: in Conan Doyle’s “The Adventure of the Dancing Men” code

The bold letters do not give you any meaningful words. So there is more to this puzzle and you need to keep looking. You will notice that the translations are in alphabetical order. This is a sign of a good puzzle where nothing is random. The alphabetical order means that you need to figure out the meaningful order.

To start, the phrases reference each other, so there is a cyclic order of reference. More importantly, the authors of the puzzle added an extra letter to each phrase. They could have put this letter anywhere in the phrase. As there is nothing random, and the placements are not the same, the index of the bold letter should provide information. If you look closely, you’ll see that the bold letters are almost all in different places. If we choose the second R in COLFERR as an extra R, then the bold letter in each text is in a different place. Try to order the phrases so that the bold letters are on the diagonal. You’ll see that this order coincides with the reference order, which gives you an extra confirmation that you are on the right track. So, let’s order:

• RBOYAL ARCH
• OAOSIS OF LIFEWATER
• MYLKO XYLOTO
• AQUAL MAGNA
• NEVEROMORE
• COLFERR
• ORANGE DYARTWING
• DOCTOR WEFRNSTROM
• ELEMENTARHY

Now the extra letters read BOKLORYFH. This is not yet meaningful, but what is this puzzle about? It is about famous substitution ciphers. The first and most famous substitution cipher is the Caesar cipher. So it is a good idea to use the Caesar cipher on the phrase BOKLORYFH. There is another hint in the puzzle that suggests using the Caesar cipher. Namely, there are many ways to clue the dancing men code. It could be Conan Doyle, Sherlock Holmes, and so on. For some reason the authors chose to use the word ELEMENTARY as a hint. Although this is a valid hint, you can’t help but wonder why the authors of the puzzle are not consistent with the hints. Again, there is nothing random, and the fact that the clues are under-constrained means there might be a message here. Indeed, the first letters read ROMAN CODE, hinting again at the Caesar shift. So you have to do the shift to arrive at the answer to this puzzle, which is ERNO RUBIK.

The most difficult puzzle I wrote for the MIT Mystery Hunt 2013 was Turnary Reasoning. I can’t take credit for the difficulty: I designed the checkers positions; they were expectedly the easiest. Timothy Chow created the chess positions, and Alan Deckelbaum created the MTG positions. As the name of the puzzle suggests, you need to find whose turn it is in each position or, as the flavor text suggests, decide that the position is impossible.

I tried to solve the chess positions myself and was charmed by their beauty. The most difficult one was the first chess puzzle presented below. Find whose turn it is or prove that the position is impossible.

The puzzle titled “50/50” was the most difficult puzzle in MIT Mystery Hunt 2013. It is a puzzle in which information is hidden in the probability distribution of coin flips. I consider it the most difficult puzzle of the hunt because it took the longest time to test-solve and we were not able to solve all four layers of the original puzzle. As a result, one of the layers was removed. I think this puzzle is very important and should be included in statistics books and taught in statistics classes. If I were ever to teach statistics, I would teach this puzzle. By the way, this elaborate monstrosity (meant as a compliment) was designed by Derek Kisman.

I am not sure that the puzzle is working on the MIT server. The puzzle is just a coin flip generator and gives you a bunch of Hs (heads) and Ts (tails). Here is the solution.

When you flip a coin, the first thing to check is the probability of heads. In this puzzle it is fifty percent as expected. Then you might check probabilities of different sequences of length 2 and so on. If you are not lazy, you will reach length 7 and discover something interesting: some strings of length seven are not as probable as expected. The two least probable strings are TTHHTTH and HTHHTTT, with almost the same probability. The two most probable strings are TTHHTTT and HTHHTTH, with the matching probability that is higher than expected. All oddly behaving strings of length 7 can be grouped in chunks of four with the same five flips in the middle. In my example above, the five middle flips are THHTT. Five flips is enough to encode a letter. The probabilities provide the ordering, so you can read a message. In the version I tested it was “TAXINUMBLOCKS.” In the current version it is “HARDYNUMBLOCKS.” Keep in mind that the message encoded this way has to have all different letters. So some awkwardness is expected. The message hints at number 1729, a famous taxicab number, which is a clue on what to do next in the second step.

What do you do with number 1729? You divide the data in blocks of 1729 and see how the k-th flip in one block correlates with the k-th flip in the next block. As expected, for most of the indices there is no correlation. But some of the indices do have correlation. These indices are close together: not more than 26 flips apart. Which means the differences will spell letters. Also, there is a natural way to find a starting point: the group of indices spans only a third of the block. In the original version the message was: “PLEASEHELPTRAPPEDINCOINFLIPPINGFACTORYJKHEREHAVEAPIECEOFPIE.”

Now I want to discuss the original version, because its solution is not available online. Here is Derek’s explanation of what happens in the third step:

So, this punny message is another hint. In fact the sequence of coin flips conceals pieces of the binary representation of Pi*e. These pieces are of length 14 (long enough to stand out if you know where to look, but not long enough to show up as significant similarities if you compare different sessions of flips), always followed by a mismatch. They occur every 1729 flips, immediately after the final position of the 1729-block message. The HERE in the message is intended to suggest looking there, but you can probably also find them (with more effort) if you search for matches with Pi*e’s digits.
The 14-flip sequences start near the beginning of the binary representation of Pi*e and continue to occur in order. (ie, every 1729 flips, 14 of them will be taken straight from Pi*e.) However, between sequences, either 1, 3, or 5 digits will be skipped. These lengths are a sequence of Morse code (1=dot, 3=dash, 5=letter break) that repeats endlessly, with two letter breaks in a row to indicate the start:
– …. ..- ..- ..- – ..- -..- ..- ..- ..- …. ..- …. – ..- ..- …. ..- ….
Translated, this gives the message “THUUUTUXUUUHUHTUUHUH”.
(Aside: I didn’t use Pi or e individually, because one of the first things I expect some teams will try is to compare the sequence of flips with those constants!)

As I said before, we didn’t solve the third step. So Derek simplified it. He replaced “PIECEOFPIE” by “BINARYPI”, and made it the digits of Pi, rather than of Pi*e. We still couldn’t solve it. So he changed the message from the second step to hint directly at the fourth step: “PLEASEHELPTRAPPEDINCOINFLIPPINGFACTORYJUSTKIDDINGTHUUUTUXUUUHUHTUUHUH.” But the binary Pi was still trapped in the coin flipping factory.

Here is Derek’s explanation of the fourth step:

Almost there! This message looks like some sort of flip sequence, because it has several Ts and Hs in there, but what of the Us and Xs? Well, U just stands for “unknown”, ie, we don’t care what goes there. And there’s only one X, so it seems significant!
The final step is to look for every occurrence of this pattern in the sequence. The flips that go where the X is are the final channel of information. You’ll find that they repeat in an unvarying pattern (no noise!) with period 323=17*19. There’s only one way to arrange this pattern into a rectangular image with a blank border, and it gives the following image:

.................

...X..XXX.XXX....

...X..X...X.X....

...X..XXX.XXX....

...X..X...XX.....

...X..X...X.X....

...X.....X.......

...X.....X.......

...X....XXX......

...X.....X.......

...X.............

...X.....XXX...X.

...X....XXXXX.XX.

..X....XX.XXXXX..

.X......XXXXXX...

.X...X.XXXXXXXX..

..XXX...XXXXX.XX.

.........XXX...X.

.................

The final answer is the French word for fish, POISSON, a word heavily related to statistics!

The answer POISSON didn’t fit in the structure of the Hunt. So Derek was assigned a different answer: MOUNTAIN. He changed the picture and it is now available in the official solution to the puzzle. He adjusted his code for coin flips so that the picture of a mountain is hidden there. But the digits of Pi are still trapped in the flips. They are not needed for the solution, but they are still there.

Derek kindly sent to me his C++ program for the latest version of the puzzle. So if the MIT website can’t generate the flips, you can do it yourself. And play with them and study this amazing example of the use of statistics in a one-of-a-kind puzzle.

When the MIT Mystery Hunt was about to end, I asked my son Sergei, who was competing with the team “Death from Above,” what his favorite puzzle was. I asked the same question to a random guy from team “Palindrome” whom I ran into in the corridor. Surprisingly, out of 150 puzzles they chose the same one as their favorite. They even used similar words to describe it. Calling it a very difficult and awesome puzzle, they both wondered how it was possible to construct such a puzzle.

The puzzle they were referring to is “In the Details” by Derek Kisman, which you can see below.

TWELEVELTWONSHELMUMUOERAIYRANL
QAPIUNPIQAYDPEPIRPRPKVOYESOYOR
ELRATFDTELDTTFDTBWNLMUTFONYDWJ
PIOYJMHAPIHAJMHAAOORRPJMYDANFC
MUOZCGTFBWIRYDHIRAIRTFNCUENCUE
RPVQUHJMAOHKANJUOYHKJMZKBNZKBN
IRONSHOZGOTFUEELTFOEELUEYDOETF
HKYDPEVQDNJMBNPIJMKVPIBNANKVJM
BWIYNLTFSHHIELTWGOYDONDTYDHIOE
AOESORJMPEJUPIQADNANYDHAANJUKV
SHDTYDRPBWUEBWIYTWTWTFYDMUELMU
PEHAANAJAOBNAOESQAQAJMANRPPIRP
ONTWELBWLMSHELTFUEBWBWLMOZEVHI
YDQAPIAOGIPEPIJMBNAOAOGIVQUNJU
DTCGUEYDRPEVNCIREVIRTWUEUETWON
HAUHBNANAJUNZKHKUNHKQABNBNQAYD
IRUERAMUTFELTWONTFOEOEEYDTNLYD
HKBNOYRPJMPIQAYDJMKVKVHWHAORAN
ELGORPNCTFDTYDSHYDELPKTFOZRACG
PIDNAJZKJMHAANPEANPIDFJMVQOYUH
DTMUWJOETFYDELMUMUGORAONIRDTCG
HARPFCKVJMANPIRPRPDNOYYDHKHAUH

_ _ _ _ _ _ _ _

The puzzle looks like a word search, but I can tell you up-front: you can’t find all the words in the grid. You can only find six words there. So there is something else to this puzzle. I will discuss the solution later. Meanwhile I will ask you very pointed questions:

• Where are the other words?
• What is the meaning of LEVEL TWO staring at us from the first row?
• Where is LEVEL ONE?
• What do these very non-random words have in common?

The easiest of the puzzles I made for the MIT Mystery Hunt 2013 was “Something in Common.” I collaborated on this puzzle with Daniel Gulotta. Ironically, it was the most time-consuming of my puzzles to design — well over a hundred hours. I can’t tell you why it took me so long without revealing hints about the solution, so I will wait until someone solves it.

I received a lot of critique from my editors for suggesting puzzles that were too easy. When, during the test-solve, I realized that this puzzle was one of the easiest in the hunt, I requested permission to make it harder. It would not actually have been difficult to make it harder: I could have just replaced some specific words with more general ones. Unfortunately, we didn’t have time for a new test-solve, so the puzzle stayed as it was. That turned out to be lucky.

This puzzle was in the last round. By the time the last round opened, we knew that the hunt was much more difficult than we had anticipated. I was afraid that people were getting angry with difficult puzzles and so I was very happy that I hadn’t changed this puzzle. By the time the teams started submitting answers to it, people were exhausted. Manic Sages increased the speed with which options to buy answers to puzzles were released. I was ecstatic that this puzzle was one of the few puzzles in the last round that was solved, not bought with options. Here is the puzzle:

• While everyone was discussing which color to paint the room, the counselor was dreaming about a real chocolate sundae. A walk-in walked into the reception in honor of a regular phenomenon visible every four hours or so. The client just wanted to find his dog in order to provide a permanent shortcut to another part of space; instead, he found something else.The Federation didn’t want to buy a lemon, so their lawyer used a spider to type the password. They discovered that the creatures glow in the dark and the perceptive negotiator won the bid. While they were waiting for the results of the shuttle trip, they turned the lights off to hunt them. The bird-like sounds were coming from under the floor. They used alcohol to save the woman’s life, which was a big mistake. She refused to be his conscience, instead she used her new untapped power of light to save the world; she already had a job as a counselor.
• Their daughter disappeared two months ago, whereas they needed to keep the wounded survivor steady. The African activist was kidnapped by rebels when she was a teenager. While some people were building a boat on the beach, she escaped from her kidnappers. He said that the reward had been withdrawn to eliminate the financial incentive to lie. They needed to perform a blood transfusion, but they didn’t have the proper instruments. By his false statement, he removed over-claimers: people lying to get attention. He needed to write vows. They read surprise at the unexpected labor in the woods in the boy’s face. It was clear that the boy had never looked into the backpack.She described horrors she had seen: rape, torture, massacres carried out by child soldiers, the doctor losing his own blood to help the wounded survivor. There was no deception leakage, but she seemed anxious, so the doctor couldn’t go and deliver the baby. They needed to find the other girl before noon, and the crushed leg made blood transfusion impractical. His vows were self-referential. He talked about how he couldn’t write the vows. While the doctor played 20 questions one man died and another was born. The girl wasn’t answering, but the doctor read her micro-expressions. The writer touched her ear and exposed her lies. At the end the doctor suspected murder, and the book was withdrawn.
• She took pictures in an abandoned house and jumped off the roof. Two girls came back to investigate. He was surprised by a basket of cookies and a statue that was in the wrong place. A new drug hit the streets making people see things, like old pictures of a woman who looked exactly like her friend. He started seeing his dead father: when people die in the past, they produce energy in the present.They were the two most powerful people on the planet. For wedding preparations she got a list of 17 DVDs. His partner started hallucinating about her ex. People do not understand time. Naomi’s ability caused all this mess: the box left them behind. The only place where she didn’t use gloves was her garden. The dinner guests tried her chicken, and, as a consequence, they were stuck looking at each other forever. The drugged cookies were a gift to help resolve their issues. Because of that, she gave him the shorthand transcripts to complete the cycle.
• Did she fall asleep while they were discussing the dead boy’s name? The price tag was exorbitant for a witness to identify the defendant. The woman would be everything he wanted and needed. She was a security guard chewing gum. The witness changed her testimony: they went to the woods and were water-rafting, rock-climbing, and arrow-shooting. As she was not the first girl he brought to the woods, the jury gave a verdict of “Not Guilty.”The detective was in court, though it wasn’t his case. She needed to stop talking and start running. Shit always rolls downhill. Poisoned water made her see things she was not supposed to remember like a shitty orange couch outside. In spite of the background check the client was a psychopath who was moved from uptown to the fucking low-rises. Shoulder to the wheel. Dead witness, mother-fucker.
• A little girl was humming about the dark side. The Wicca group was boring, and the new invention was making whooshing sounds. While a laryngitis epidemic took over the town, the noise-eater got turned on by accident.The princess’s scream would kill the monsters, while the monster machine killed its own remote control. She and her future boyfriend discovered each other’s secrets. The dark side is waiting.
• The experiment in the gay club was very important to him. He was a semi-cute boy-next-door type and his shuttle trip was supposed to be easy. There is more to a guy than cock size, and he was being pulled. He was injected with something and started to understand everyone. They were a bald priestess and a warrior with a very nice butt. They offered you a discount if you bought the butt and the bulge together.They were approaching a commerce planet in Pennsylvania. They escaped and were standing on the roof of a hospital. She was sending a transmission, while the older man was running his tongue along the young man’s spine. The girl tried to protect him, believing his story, but was arrested for contamination. Fuck. He had a baby, two babies. He distracted the guards with a puzzle ring. And while they were painting his black car with a pink derogatory word, they escaped.
• He was drinking before operating on his fiancée. What kind of a father kills people? Tonight was the night he would finally sleep, and drinking was the only way for him to stop his hands from shaking. The limo driver kidnapped him while she watched herself die in the mirror. While being sleep-deprived he conducted a test. Nothing was wrong, except he brought the wrong documents to court. The criminal walked, but, unexpectedly, he couldn’t feel his leg and couldn’t walk anymore. There was a lot of blood and the body was not filtering iodine. He took a picture of the actor falling into a coma with his blood-spatter camera.His girlfriend wanted to buy a firm mattress to have sex. He preferred to sleep on a water-bed and told the secret of his bloody hobby to his baby. It was not an infection, it was an allergy, so he changed his plan of where to grab the victim. The case was solved because of the bubbles in the glass. He was killing for his son now. The patient was indeed allergic and crashed his car.
• The woman died two weeks ago, but her car accident was yesterday. There was so much blood and, for some reason, ice. Jane Doe wasn’t the girl’s sister. Melting speed and surface tension could help the calculation. They came to pay their respects but the celebration was postponed. They brought personal effects to drop off. If the couple’s daughter was like their mother, then they themselves were like their grandparents. The idea to ask the grandmother resulted in a kiss.Their planet had been on the verge of a golden age, then everything fell apart. She brought some clothes, a toothbrush, shampoo and some other things to the detention center. “Don’t let the history repeat itself,” the worshiper of the second in command said. She didn’t know what the red string was for. The teen’s sister told him stories about another galaxy, and the war and the algorithm that might find the dead man’s favorite coffee place and, consequently, solve the case. The kidney operation was in a hotel. They didn’t expect to see the body, but there it was. She touched the body to reveal emptiness inside. At the end they gathered in his house for dinner as usual. He had to save Courtney’s future body before everything blew up and put the red sticker on his license.
• After retirement, he came back to an unsolved murder case; he remembered a kiss in flashbacks. He drove to the lake where the accidental drowning happened. He lured everyone involved to the lake, and, after having sex, he told her that he wanted a real marriage. They wanted their child to be born on the new planet. The doctor was one of the suspects. The couple was already in the cabin, and he doubted that he was the one who she really wanted.The young man was murdered, and everyone thought that the detective was the real target. The man went to look for sneakers during the boxing match. The nosy lady-writer dropped names to persuade the sheriff to look into the cabin. The admiral challenged the chief to join him in the ring. They didn’t find the sneakers, and they shouted this to the skies. The lady solved the murder, as usual, while the boxing match became too personal and people started leaving.

The second “instructioned” puzzle is Portals by Palmer Mebane. It is an insanely beautiful and difficult logic puzzle that consists of known puzzle types interconnected to each other through portals. Here Palmer Mebane explains how portals work:

“Each of the ten puzzles corresponds to a color, seen above the grid where the name of the puzzle is written. The grid contains nine square areas, one each of the other nine colors. These are portals that connect the puzzle to one of the other nine, as denoted by the portal color. Each puzzle’s rules define which squares of their solution are “black”. On the portal squares, the two puzzles must agree on which squares are black and which are not. For instance, if in the red grid the top left square of the blue portal is black, then in the blue grid the top left square of the red portal must also be black, and vice versa.”

On the Portals puzzle page you can find the rules for how each individual game is played and how to shade areas. The puzzle requires a lot of attention. It took us a long time to test-solve it. If you make a mistake in one grid it will propagate and will lead to a contradiction in another grid, so it is difficult to correct mistakes. If you do make a mistake, you are not alone: we kept making mistakes during our test-solve. Because of the difficulty of tracing back to the source of the error, we just started anew, but this time making sure that every step was confirmed by two people. Working together in this way, we were able to finish it.

If you do not care about the extraction and the answer, ignore the letter grid in the middle and enjoy the logic of it.

There were a couple of puzzles during the MIT Mystery Hunt that were not so mysterious. Unlike in traditional hunt puzzles, these puzzles were accompanied by instructions. As a result you can dive in and just enjoy solving the logic part of the puzzle without bothering about the final phase, called the extraction, where you need to produce the answer.

The first puzzle with instructions is Random Walk by Jeremy Sawicki. I greatly enjoyed solving it. In each maze, the goal is to find a path from start to finish, moving horizontally and vertically from one square to the next. The numbers indicate how many squares in each row and column the path passes through. There are nine mazes in the puzzle of increasing difficulty. I am copying here two such mazes: the easiest and the toughest. The colored polyomino shapes are needed for the extraction, so you can ignore them here.

Today I have a special treat for you. Here is the first of several puzzles that I plan to present from the 150 that we used in the MIT Mystery Hunt 2013. Keep in mind that although the puzzles have authors, they were the result of a collaboration of all the team members. In many instances editors, test-solvers and fact-checkers suggested good ways to improve the puzzles.

I wrote the puzzle Open Secrets jointly with Rob Speer. The puzzle was in the opening round, which means it is not too difficult. By agreement the answers to the puzzles are words or phrases. I invite my readers to try this puzzle. I will post the explanation in about two weeks.

I dropped my blog for two months. Some of my readers got worried and wrote to ask if I was okay. Thanks for your concern.

I am okay. I was consumed by the MIT Mystery Hunt. My team, Manic Sages, won the hunt a year ago, and as a punishment — oops, I meant as a reward — we got to write the 2013 hunt, instead of competing in it. I myself ended up writing about ten problems for the hunt. This was in addition to test-solving about 150 problems my whole team prepared for the hunt.

I could only think about the hunt. My mind was full of ideas for the hunt so I was afraid to write in my blog about something that I might later want to use for my problems. Or even worse, I was nervous that my blog posts might be unconsciously revealing hunt secrets. Moreover, I didn’t want to advertise the fact that I was working on the hunt, thereby drawing people to my blog to scrutinize my interests as they prepared for the hunt.

So I just disappeared.

I apologize; please forgive me.