A Measure of Central Symmetry
Consider central symmetry: squares and circles are centrally symmetric, while trapezoids and triangles are not. But if you have two trapezoids, which of them is more centrally symmetric? Can we assign a number to describe how symmetric a shape is?
Here is what I suggest. Given a shape A, find a centrally symmetric shape B of the largest area that fits inside. Then the measure of central symmetry is the ratio of volumes: B/A. For centrally symmetric figures the ratio is 1, and otherwise it is a positive number less than 1.

The measure of symmetry is positive. But how close to 0 can it be? The picture on the left is a shape that consists of five small disks located at the vertices of a regular pentagon. If the disks are small enough than the largest symmetric subshape consists of two disks. Thus the measure of symmetry for this shape is 2/5. If we replace a pentagon with a regular polygon with a large odd number of sides, we can get very close to 0.
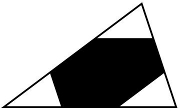
What about convex figures? Kovner’s theorem states that every convex shape of area 1 contains a centrally symmetric shape of area at least 2/3. It is equal to 2/3 only if the original shape is a triangle. That means every convex shape is at least 2/3 centrally symmetric. It also means that the triangle is the least centrally symmetric convex figure. By the way, a convex shape can have only one center of symmetry.
After I started writing this I discovered that there are many ways in which people define measures of symmetry. The one I have defined here is called Kovner-Besicovitch measure. The good news is that the triangle is the least symmetric planar convex shape with respect to all of these different measures.
Share:
Tanya Khovanova:
Sam reminded me that the shapes in consideration are BOUNDED.
3 September 2012, 10:52 amSlaz:
I’d like to read more about this central symmetry. How is it applied? I guess physics is a safe guess, but would like to hear a more in-depth explanation.
1 November 2012, 8:30 am