Archive for the ‘Puzzles’ Category.
2nd September 2012, 06:20 pm
Consider central symmetry: squares and circles are centrally symmetric, while trapezoids and triangles are not. But if you have two trapezoids, which of them is more centrally symmetric? Can we assign a number to describe how symmetric a shape is?
Here is what I suggest. Given a shape A, find a centrally symmetric shape B of the largest area that fits inside. Then the measure of central symmetry is the ratio of volumes: B/A. For centrally symmetric figures the ratio is 1, and otherwise it is a positive number less than 1.

The measure of symmetry is positive. But how close to 0 can it be? The picture on the left is a shape that consists of five small disks located at the vertices of a regular pentagon. If the disks are small enough than the largest symmetric subshape consists of two disks. Thus the measure of symmetry for this shape is 2/5. If we replace a pentagon with a regular polygon with a large odd number of sides, we can get very close to 0.
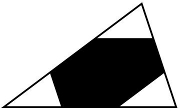
What about convex figures? Kovner’s theorem states that every convex shape of area 1 contains a centrally symmetric shape of area at least 2/3. It is equal to 2/3 only if the original shape is a triangle. That means every convex shape is at least 2/3 centrally symmetric. It also means that the triangle is the least centrally symmetric convex figure. By the way, a convex shape can have only one center of symmetry.
After I started writing this I discovered that there are many ways in which people define measures of symmetry. The one I have defined here is called Kovner-Besicovitch measure. The good news is that the triangle is the least symmetric planar convex shape with respect to all of these different measures.
Share:





20th August 2012, 03:01 pm
 I received the book Taking Sudoku Seriously by by Jason Rosenhouse and Laura Taalman for review and put it aside to collect some dust. You see, I have solved too many Sudokus in my life. The idea of solving another one made me barf. Besides, I thought I knew all there is to know about the mathematics of Sudoku.
I received the book Taking Sudoku Seriously by by Jason Rosenhouse and Laura Taalman for review and put it aside to collect some dust. You see, I have solved too many Sudokus in my life. The idea of solving another one made me barf. Besides, I thought I knew all there is to know about the mathematics of Sudoku.
One day out of politeness or guilt I opened the book — and couldn’t stop reading.
The book is written for people who like Sudoku, but hate math. This is so strange. Sudoku is math. People who are good at Sudoku are good at math, or at least they are supposed to be. It seems that math education in the United States is so bad that people who were born to be good at math and to like math, hate it instead. So the goal of the book is to establish a bridge from Sudoku to math. And the book does a superb job of it.
This well-written book moves from puzzles to discussions in such a natural way that math becomes a continuation of puzzles.
Taking Sudoku Seriously covers a lot of fun material: methods to solve Sudoku, how to count the number of different Sudoku puzzles, and how to find the smallest number of clues that are needed for a unique puzzle. The book travels into the neighboring area of Latin and Greco-Latin squares. While discussing all those fun things it covers groups, symmetries, number theory, graph theory (including book thickness) and more.
I am not the target audience for this book, because I do not need convincing that math is fun. The best part for me was the hundred puzzles. Only a portion of them were standard Sudoku puzzles — and I skipped those. The others were either Sudoku with a twist or plain math puzzles.
The puzzles are all very different and I was so excited by them, that I went ahead and solved them, and caught up with reading the text later. And I enjoyed both: reading and solving.
Here is puzzle 91 from the book. Fill in the grid so that every row, column, and block contains 1-9 exactly once. In addition, each worm must contain entries that increase from tail to head. For blue worms you must figure out yourself which end is the head.
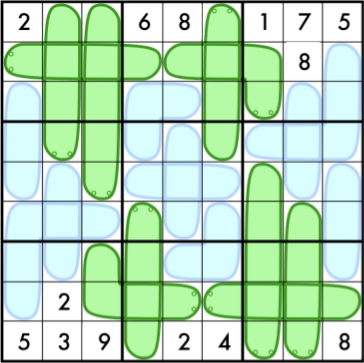
Share:





9th August 2012, 05:07 pm
It’s easy to judge who is the fastest runner or swimmer. Judges do not need to be runners and swimmers themselves. They simply need a stopwatch and a camera.
Other competitions are more difficult to judge. Take for example the Fields medal. The judges need to be mathematicians. Since they can’t be experts in all the different areas of mathematics, they have to rely on recommendation letters. The mathematicians who write recommendation letters are biased, because they are interested in promoting their own field. The committee’s job is not simple, not the least because it involves a lot of politics. It is easy to award the medal to Grigory Perelman. He solved a high-profile long-standing conjecture. But other cases are not that straightforward.
Imagine a genius mathematician with a new vision. He or she might be so far ahead of everyone else, that the Fields committee would fail to appreciate the new concept. I wish the math community would create a list of mathematicians who deserved the Fields medal, but were passed over. As time goes by, perhaps a new Einstein will emerge on this list.
The reason the Fields committee more or less works is that the judges do not need to be as talented mathematicians as the awardees. They do not need to create mathematics, they need to understand it. And the latter is easier than the former.
A completely different story happens with IQ tests. Someone has to write those tests. There is no reason to think that writers of the IQ tests are anywhere close to the end tail of the IQ distribution. Hence, the IQ tests are not qualified to find the IQ geniuses.
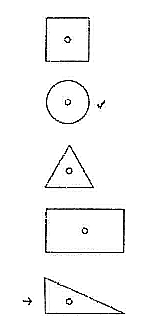
Now might be a good time to complain about the IQ test I took myself. Many years ago I tried an IQ test online through tickle.com. I was so disappointed with my non-perfect score that I never looked at my answers. Recently, while cleaning my apartment, I discovered the printout of the test. I made one mistake in the following question.
Which one of the designs is least like the other four?
The checkmark is the expected answer. They think that the circle is the odd one out because all the other shapes are polygons. The arrow points to my answer. I chose the right triangle because it is the only shape without symmetries. Who says that polygonality is more important than symmetry?
Share:





29th July 2012, 12:52 pm
Kvant is a very popular Russian math and physics journal for high school-children. My favorite page is the one with puzzles directed to younger readers. Here are two puzzles from the latest online issue: 2012 number 3.
The first one, by N. Netrusova, is optimistic about the next year.
An astrologist believes that a year is happy if its digit representation contains four consecutive digits. For example, the next year, 2013, will be happy. When was the previous happy year?
The second problem is by L. Mednikov and A. Shapovalov. It confused me at first. For a moment I thought that the best answer is 241 rubles:
A big candle lasts one hour and costs 60 rubles. A small candle lasts 11 minutes and costs 11 rubles. Can you measure a minute by spending not more than a) 200 rubles, b) 150 rubles?
Share:





22nd July 2012, 12:32 pm
 Do you like challenging puzzles? Are you tired of sudoku? Here’s your chance to try your hand at puzzles that are designed for world puzzle championships.
Do you like challenging puzzles? Are you tired of sudoku? Here’s your chance to try your hand at puzzles that are designed for world puzzle championships.
I’ve already done the homework for you — and it turned out to be more complicated than I anticipated. The world puzzle federation has a website, but unfortunately they are lazy or secretive. It is difficult to find puzzles there. A few puzzles are available in the World Puzzle Federation Newsletters.
Since I am stubborn, I spent a lot of time looking for championship puzzles. I found them in books. Here is the list I compiled so far. If you too are interested in high-level puzzles, this ought to make your search a lot easier. The book titles are confusing, so I added a description of what’s in them.
- Games Magazine Presents Brain Twisters from the First World Puzzle Championships — Warm-up puzzles, US/Canada Qualifying test, First World Championship, Foreign team puzzles.
- Games Magazine Presents Brain Twisters from the World Puzzle Championships, Volume 2 — US/Canada Qualifying test, Second World Puzzle Championship, Third World Puzzle Championship.
- Games Magazine Presents Brain Twisters from the World Puzzle Championships, Volume 3 — Fourth World Puzzle Championship, Fifth World Puzzle Championship.
- World Puzzle Championships Omnibus, Volume 1 — Contains World-Class Puzzles from the World Puzzle Championships Volumes 1-3 below.
- World-Class Puzzles from the World Puzzle Championships, Volume 1 — Sixth World Puzzle Championship and Seventh World Puzzle Championship.
- World-Class Puzzles from the World Puzzle Championships, Volume 2 — 1999 Qualifying test, Eighth World Puzzle Championship.
- The New York Times Sunday Crossword Omnibus, Volume 3 — 2000 Qualifying test, Ninth World Puzzle Championship.
- World-Class Puzzles from the World Puzzle Championships, Volume 4 — 2001 Qualifying test, Tenth World Puzzle Championship.
- World-Class Puzzles from the World Puzzle Championships, Volume 5 — 2002 Qualifying test, Eleventh World Puzzle Championship.
- Random House World-Class Puzzles — 2002 Qualifying test, Twelfth World Puzzle Championship. (The year for the qualifying test is probably a typo as puzzles differ from the qualifying test in the previous book,)
One of my favorite puzzle types is Easy as ABC. You have to fill one of A, B, C, and D in each row and column. The letters outside the grid indicate which letter you see first from that direction. Here is one from the 2011 newsletter:
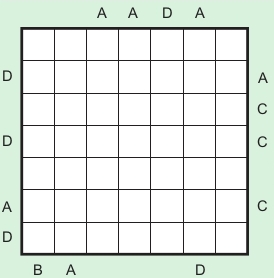
Share:





9th May 2012, 01:29 pm
Baron Münchhausen is famous for his tall tales. My co-author Konstantin Knop wants to rehabilitate him and so invents problems where the Baron is proven to be truthful from the start. We already wrote a paper about one such problem. Here is a new problem by Konstantin:
Kostya has a black box, such that if you put in exactly 3 coins of distinct weights, the box will expose the coin of median weight. The Baron gave Kostya 5 coins of distinct weights and told him which coin has the median weight. Can Kostya check that the Baron is right, using the box not more than 3 times?
Actually, Konstantin designed a more complicated problem that was given at the Euler Olympiad, 2012 in Russia.
Let n be a fixed integer. Kostya has a black box, such that if you put in exactly 2n+1 coins of distinct weights, the box will expose the coin of median weight. The Baron gave Kostya 4n+1 coins of distinct weights and told him which coin has the median weight. Can Kostya check that the Baron is right, using the box not more than n+2 times?
Note that Kostya can’t just put 4n+1 coins in the box. The box accepts exactly 2n+1 coins. The problem that I started with is for n = 1. Even such a simple variation was a lot of fun for me to solve. So, have fun.
Share:





2nd May 2012, 10:15 am
Once upon a time there was a land where the only antidote to a poison was a stronger poison, which needed to be the next drink after the first poison. In this land, a malevolent dragon challenges the country’s wise king to a duel. The king has no choice but to accept.
By bribing the judges, the dragon succeeds in establishing the following rules of the duel: Each dueler brings a full cup. First they must drink half of their opponent’s cup and then they must drink half of their own cup.
The dragon wanted these rules because he is able to fly to a volcano, where the strongest poison in the country is located. The king doesn’t have the dragon’s abilities, so there is no way he can get the strongest poison. The dragon is confident of winning because he will bring the stronger poison.
The only advantage the king has is that the dragon is dumb and straightforward. The king correctly predicts what the dragon will do. How can the king kill the dragon and survive?
Share:





1st May 2012, 07:28 pm
There is an array containing all the integers from 1 to n in some order, except that one integer is missing. Suggest an efficient algorithm for finding the missing number.
A friend gave me the problem above as I was driving him from the airport. He had just been at a job interview where they gave him two problems. This one can be solved in linear time and constant space.
But my friend was really excited by the next one:
There is an array containing all the integers from 1 to n in some order, except that one integer is missing and another is duplicated. Suggest an efficient algorithm for finding both numbers.
My friend found an algorithm that also works in linear time and constant space. However, the interviewer didn’t know that solution. The interviewer expected an algorithm that works in n log n time.
The company claims that they are looking for the smartest people in the world, and my friend had presented them with an impressive solution to the problem. Despite his excitement, I predicted that they would not hire him. Guess who was right?
I reacted like this because of my own story. Many years ago I was interviewing for a company that also wanted the smartest people in the world. At the interview, the guy gave me a list of problems, but said that he didn’t expect me to solve all of them — just a few. The problems were so difficult that he wanted to sit with me and read them together to make sure that I understood them.
The problems were Olympiad style, which is my forte. While we were reading them, I solved half of them. During the next hour I solved the rest. The interviewer was stunned. He told me of an additional problem that he and his colleagues had been trying to solve for a long time and couldn’t. He asked me to try. I solved that one as well. Guess what? I wasn’t hired. Hence, my reaction to my friend’s interview.
The good news: I still remember the problem they couldn’t solve:
A car is on a circular road that has several gas stations. The gas stations are running low on gas and the total amount of gas available at the stations and in the car is exactly enough for the car to drive around the road once. Is it true that there is a place on the road where the car can start driving, stopping to refuel at each station, so that the car completes a full circle without running out of gas? Assume that the car’s tank is large enough not to present a limitation.
Share:







 I received the book
I received the book 

 Do you like challenging puzzles? Are you tired of sudoku? Here’s your chance to try your hand at puzzles that are designed for world puzzle championships.
Do you like challenging puzzles? Are you tired of sudoku? Here’s your chance to try your hand at puzzles that are designed for world puzzle championships.