Another Russian Olympiad
I found a new Russian Olympiad for high schools related to universities. I translated my favorite problems from last year’s final round. These are the math problems:
8th grade. In a certain family everyone likes their coffee with milk. At breakfast everyone had a full cup of coffee. Given that Alex consumed a quarter of all consumed milk and one sixth of all coffee, how many people are there in the family?
8th grade. How many negative roots does the equation x4 − 5x3 − 4x2 − 7x + 4 = 0 have?
10th grade. Find a real-valued function f(x) that satisfies the following inequalities for any real x and y: f(x) ≤ x and f(x+y) ≤ f(x) + f(y).
I liked the physics problems even more:
8th grade. Winnie-the-Pooh weighs 1 kg. He hangs in the air with density 1.2kg/m3 next to a bee hive. He is holding a rope connected to a balloon. Estimate the smallest possible diameter of the balloon, assuming that this happens on Earth.
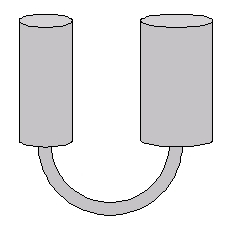
Share:10th grade. Two containers shaped like vertical cylinders are connected by a pipe underneath them. Their heights are the same and they are on the same level. The cross-sectional area of the right container is twice bigger than the left’s. The containers are partially filled with water of room temperature. Someone put ice into both containers: three times more ice into the right one than into the left one. After that, the containers are closed hermetically. How will the water level will change after the ice melts completely:
- The levels will not change.
- The level on the left will be higher than on the right.
- The level on the left will be lower than on the right.
- The answer depends on the initial volume of water in the containers.
Alex:
Am I missing something or is there a stunningly obvious answer for the 10th grade math problem?
Loved the first 8th grade problem. Still working on the second.
17 November 2011, 5:05 pmKevin:
@Alex: I think the inequalities are supposed to be strict inequalities, otherwise f(x) = x is a trivially easy solution.
17 November 2011, 6:04 pmTanya Khovanova:
Alex, Kevin,
You are supposed to find all possible functions.
17 November 2011, 6:38 pmAlex:
@Kevin — the inequalities can’t be strict because the first implies f(0) = 0.
Finding *all* solutions does make it a more interesting problem, and much more challenging.
17 November 2011, 8:00 pmAlex:
Should have known that my < and > signs would get taken out.
What I meant to say was that the first implies f(0) <= 0 and the second implies f(0) >= 0.
Did that come out right?
17 November 2011, 8:01 pmAustin:
The first 8th grade math problem is brilliant in its simplicity. Even better is the fact that we can compute the relative proportions of coffee and milk in Alex’s cup!
17 November 2011, 9:45 pmAlex:
Okay, I finally got the other two math problems. These were really fun, thanks for posting them.
I’m kinda new here, should I be solving these in the comments, or will people complain about spoilers if I do that?
18 November 2011, 12:33 pmRichard:
For fun, I looked for a proof that x^4-5x^3-4x^2-7x+4 has no negative roots that didn’t require calculus or the quartic equation. I found a nifty one that combines the first, third, and fifth terms.
This is for 8th graders after all.
21 November 2011, 8:24 amSachin:
The 10th grade physics question is very interestingly posed. Isn’t the problem essentially the same as adding some water to one of the cylinders?
22 November 2011, 2:24 pmPratik Poddar:
For the first eight grade question,
Let the total milk consumed be m and the total coffee consumed be c
m/4 + c/6 = 1 cup
Total number of cups consumed = m+c = t
t – c/3 = 4
t + m/2 = 6
Since t is an integer, and t > 4 and t < 6
We get t = 5. Total number of people in the family = 5 🙂
Nice problem. Thanks
14 December 2011, 6:32 amSam:
For the first 10th grade question:
25 November 2012, 5:34 pmIf f(x) <= x and f(x + y) <= f(x) + f(y) for all real x and y, then consider x = y = 0. Because f(0) = 0. But we know that f(0) <= 0, so f(0) = 0. Now consider real numbers a and -a. We know that f(0) <= f(a) + f(-a) so 0 <= f(a) + f(-a). But f(a) <= a and f(-a) <= -a, so f(a) + f(-a) <= 0, which means that f(a) + f(-a) = 0, and we can conclude that the ONLY function that satisfies the requirements is f(x) = x
Sam:
For the last comment, when I write “Because f(0) = 0” in the second sentence I mean “Because f(0) 0” I don’t know why that part got deleted. Sorry
25 November 2012, 5:38 pmSam:
It changed it again. I am very sorry for spamming your comments page Tanya, but it changes a sentence that I write to f(0) 0. Hopefully, your readers can figure out what I am trying to do.
25 November 2012, 5:40 pmM Minar:
8th grade math problem:
The wording of the problem and underlying assumptions make this problem challenging on many levels. I find that this is a common theme with “excellent” problems; one has to assume certain truths that will make the problem solvable, otherwise it would be intractable.
Does LaTeX work in your blog? I’m testing here: $latex frac{5}{8}$
9 December 2012, 4:39 pm