Tanya Khovanova's Math Blog

I found the following puzzle on a facebook page of Konstantin Knop (in Russian):

Seven astronauts landed on a small spherical asteroid. They wanted to explore it and walked in different directions starting from the same location. All used the same walking algorithm: walk x kilometers forward, turn 90 degrees left and walk another x kilometers, turn 90 degree left again and walk the last x kilometers. The value of x was different for different astronauts and was one of 30, 40, 50, 60, 70, 80, and 90.
All but one astronaut finished in the same location. What was the value of x for the astronaut who finished alone? What is the size of the asteroid?

Russians cherish the issues of Kvant, a famous Soviet monthly magazine for high-school students devoted to math and physics. At its peak its circulation was about 300,000, which is unparalleled for a children’s science journal. I still have my old childhood issues somewhere in my basement. But one issue is very special: it has a prominent place in my office. I didn’t receive it by subscription; I received it as a gift from my brother Misha.

Strictly speaking Misha is not my brother, but rather a half-brother. His full name is Mikhail Khovanov and he is a math professor at Columbia. The signed issue he gave me contains his math problem published in the journal. He invented this problem when he was a 10th grader. Here it is:

In a convex n-gon (n > 4), no three diagonals are concurrent (intersect at the same point). What is the maximum number of the diagonals that can be drawn inside this polygon so that all the parts they divide into are triangles?

He designed other problems while he was in high school. All of them are geometrical in nature. The journal is available online, and a separate document with all the math problems is also available (in Russian). His problems are M1038, M1103, M1108 (above), M1119, M1153, M1204. I like his other problems too. M1153 (below) is the shortest problem on his list: as usual I am guided by my laziness.

What’s the greatest number of turns that a rook’s Hamiltonian cycle through every cell on an 8 by 8 chessboard can contain?

I wanted to accompany this post with a picture of my brother at the age he was when he invented these problems—about 16. Unfortunately, I don’t have a quality picture from that period. I do have a picture that is slightly off: by about ten years.

In the starting position you see four multi-colored quadrants of a ring. For example, the first picture shows the starting position of level 33.

You can either swipe or touch between the quadrants. A swipe expands one quadrant into two quadrants and compresses two other quadrants into one. You can swipe clockwise or counterclockwise. The second figure shows the result of the clockwise swipe of the North opening. The NW quadrant that was half-red and half-yellow has expanded into two quadrants. The red piece now occupies the entire NW quadrant and the yellow piece—the entire NE quadrant. Two East quadrants got contracted into one SE quadrant. The former blue NE quadrant became the top blue half of the SE quadrant. The former SE half-blue half-green quadrant became the bottom half of the SE quadrant. In general the quadrant where the swiping movement starts expands in the direction of the swipe and the quadrant where the swiping movements ends together with the next quadrant compresses.

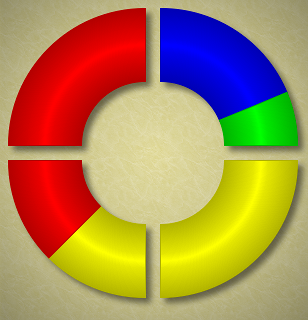
You can also touch an opening between quadrants. In this case the neighboring quadrants exchange places. The third figure shows the result of touching the East opening.

The goal of the game is to reach the final position: have each quadrant in one color. The next image shows the end of this particular level. As you can see the game was finished in 7 moves. In this particular case this is the smallest number of moves possible. To tell you a secret, it wasn’t me who finished the game in the smallest number of moves: it was my brother.

There is also a tutorial for this game on youtube.

I recently posted two trick questions.

First question. What is the answer to this question?

The title to this post was the same as the content except for the question mark: What is the Answer to This Question. The title contained the answer: WHAT.

What I like about trick questions is that sometimes people produce alternative answers that are as good as the intended ones. For this problem I like the following answers:

• If you have a compiler which converts recursion to loops, then infinite loop. Otherwise, stack overflow. (by aphar)
• Chocolate is the answer. It doesn’t matter what the question is. (by Mark James)
• 42. (by Clao)
• This is the Answer to that Question. (by Javifields)

Second question. How many letters are there in the correct answer to this question?

The intended answer was FOUR, as four is the only number in the English language for which the number of letters in its name is equal to the number itself. Many people used variations on the theme and supplied the following answers by writing out numbers in non-canonical ways:

• Positive fifteen. (by my AMSA students)
• One plus twelve. (by Michael and MQ)
• Two plus eleven. (by MQ)
• Maybe eleven. (by Michael Albert)
• Certainly sixteen. (by Michael Albert)
• Zero plus one plus two plus three plus …. (by Bob Hearn)

Some people used sentences to express numbers:

• Any number n whose value can be expressed using n letters, for example sixty seven. (by Michael Albert)

Some other people used Roman numerals and digits to express the answer:

• I, II, or III (by my AMSA students)
• 0 (by my AMSA students, Leo, and lvps1000vm)

Many people pointed out that if the puzzle would be asked in other languages, it would produce completely different answers.

But the majority of my AMSA students took a completely different approach:

• 30.

This is because there are thirty letters in the phrase the correct answer to this question.

The first Moscow Math Olympiad was conducted in 1935. Today, eighty years later, I decided to check it out. Most of the problems look standard, but some of the stereometry problems look too complicated. I found four problems that I really like: all of them are geometry problems.

Problem 1. The lengths of the sides of a triangle form an arithmetic progression. Prove that the radius of the inscribed circle is one third of one of the heights of the triangle.

Problem 2. A median, bisector, and height all originate from the same vertex of a triangle. You are given the three points that are the intersection points of the aforementioned median, bisector, and height with the circumscribed circle. Construct the triangle.

Problem 3. Find the set of points P on the surface of a cube such that the main diagonal subtends the smallest possible angle if viewed from P. Prove that the main diagonal subtends larger angles if viewed from other points on the surface. [Clarification: the two corners the main diagonal passes through don’t count.]

Problem 4. Given three parallel straight lines, construct a square such that three of its vertices belong to these lines.

Each of these problems has a powerful idea that solves it. You can try and solve these problems, but if you want help, the ideas are presented below as hints in a scrambled order.

• Hint. Rotate by 90 degrees.
• Hint. Consider a circumscribed sphere.
• Hint. The line connecting the intersection point of the bisector with the circle and the circle’s center is parallel to the height.
• Hint. Use Heron’s formula.

How many letters are there in the correct answer to this question?

What is the answer to this question?

Round 1 of Who Wants to Be a Mathematician had the following math problem:

Bob and Jane have three children. Given that one child is their daughter Mary, what is the probability that Bob and Jane have at least two daughters?

In all such problems we usually make some simplifying assumptions. In this case we assume that gender is binary, the probability of a child being a boy is 1/2, and that identical twins do not exist.

In addition to that, every probability problem needs to specify the distribution of events over which the probability is calculated. This problem doesn’t specify. This is a mistake and a source of confusion. In most problems like this, the assumption is that something is chosen at random. In this type of problem there are two possibilities: a family is chosen at random or a child is chosen at random. And as usual, different choices produce different answers.

The puzzle above is not well-defined, even though this is from a contest run by the American Mathematical Society!

Here are two well-defined versions corresponding to two choices in randomization:

Bob and Jane is a couple picked randomly from couples with three children and at least one daughter. What is the probability that Bob and Jane have at least two daughters?

Mary is a girl picked randomly from a pool of children from families with three children. What is the probability that Mary’s family has at least two daughters?

Now, if you don’t mind, I’m going to throw in my own two cents, that is to say, my own two puzzles.

Harvard researchers study the influence of identical twins on other siblings. For this study they invited random couples with three children, where two of the children are identical twins.

1. Bob and Jane is a couple picked randomly from couples in the study with at least one daughter. What is the probability that Bob and Jane have at least two daughters?
2. Mary is a girl picked randomly from a pool of children participating in the study. What is the probability that Mary’s family has at least two daughters?

The puzzle Family Ties was written for the 2013 MIT Mystery Hunt, but it never made it to the hunt. Here’s your chance to solve a puzzle no one has seen before. I wrote the puzzle jointly with Adam Hesterberg. The puzzle is below:

Mathematics professor S. Lee studies genealogy and is interested in the origins of life.

1. Alexei Mikhailovich Ivanov
2. Alexei Petrovich Ivanov
3. Amminadab
4. Anna of Moscow
5. Arador
6. Arahad II
7. Arassuil
8. Arathorn I
9. Arathorn II
10. Aravorn
11. Argonui
12. Asger Thomsen
13. Caecilia Metella Dalmatica
14. Egmont
15. Eldarion
16. Ellesar
17. Endeavour
18. Faustus Cornelius Sulla
19. Henry Frederick
20. Hezron
21. Isaac
22. Ivan the Great
23. Ivan the Terrible
24. Jacob
25. James I and VI
26. James V
27. Jens Knudsen
28. John Francis
29. Joseph Patrick
30. Joseph Patrick
31. Jørgen Jensen
32. Judah
33. Knud Nielsen
34. Margaret Stuart
35. Maria Donata
36. Mary Stuart
37. Matthew Rauch
38. Mikhail Ivanovich Ivanov
39. Niels Møller
40. Ole Pedersen
41. Peder Petersen
42. Peter Jørgensen
43. Petr Alexeyevich Ivanov
44. Pharez
45. Ram
46. Robert Francis
47. Rose Elizabeth
48. Søren Thomsen
49. Thomas Olsen
50. Ursula Gertrud
51. Vasily I of Moscow
52. Vasily II of Moscow
53. Vasili III of Russia
54. Yuri of Uglich
55. Zerah

I already wrote about my favorite problem from the 2015 All-Russian Math Olympiad that involved tanks. My second favorite problem is about coins. I do love almost every coin problem.

A coin collector has 100 coins that look identical. He knows that 30 of the coins are genuine and 70 fake. He also knows that all the genuine coins weigh the same and all the fake coins have different weights, and every fake coin is heavier than a genuine coin. He doesn’t know the exact weights though. He has a balance scale without weights that he can use to compare the weights of two groups with the same number of coins. What is the smallest number of weighings the collector needs to guarantee finding at least one genuine coin?