In Search of a Tribonacci Building
The Wythoff array is an array of integers that can be defined through Wythoff’s game. For my purposes, I will skip over Wythoff’s game and define his array using Fibonacci numbers.
You probably heard about binary, ternary, decanary, and other bases. I am sure you know the decanary base: it is our standard decimal system. But, have you ever heard about the Fibonacci base?
Let me define it. Any positive integer can be represented uniquely as a sum of distinct Fibonacci numbers that are not neighbors. For example, 16 is 13 + 3. Now, we just write ones for Fibonacci numbers that we used and zeros for unused Fibonacci numbers, so that the digit corresponding to Fibonacci number 1 is last. (The digit corresponding to Fibonacci number 2 is second to last). Thus, 16 in the Fibonacci base is 100100. The result looks like binary, but it will never have two consecutive ones. Such a representation is called the Zeckendorf representation.
What happens if we add 0 at the end of a number in its Zeckendorf representation? This is like multiplying by 2 in binary. But, in the Fibonacci base, it corresponds to replacing every Fibonacci number in the sum with the next Fibonacci number. The result is called the Fibonacci successor. For example, the Fibonacci successor of 16 has the Zeckendorf representation 1001000 and is equal to 21 + 5 = 26.
Now back to the Wythoff array. The first row consists of the Fibonacci numbers in order. Their Zeckendorf representations look like powers of two in binary. The first column consists of numbers ending in 1 in the Zeckendorf representation, in increasing order. In other words, the Zeckendorf representations of numbers in the first column resemble odd numbers in binary. To finish the definition of the array, each number in the nth column is the Fibonacci successor of a number to its left.
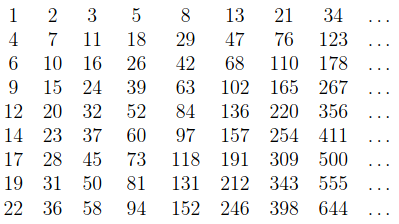
As an example, let’s calculate the first three numbers of the second row. The smallest number that is not a Fibonacci number and looks odd in its Zeckendorf representation is 4, represented as 101 (remember, we are not allowed to have two consecutive ones). We place 4 in the first column of the second row. The next number in the second row has to be the Fibonacci successor of 4, so its Zeckendorf representation has to be 1010. This number equals 5+2 = 7. The Fibonacci successor of 7 is 11, with Zeckendorf representation 10100.
John Conway and Alex Ryba wrote a paper where they studied the Wythoff array. They continued the array to the left and drew walls according to a few rules. Here is a picture of their result. The picture is too small to make out the numbers, but you can see the shape, which looks like the Empire State Building. Oops, I forgot to mention, the paper is called The Extra Fibonacci Series and the Empire State Building.

My last year’s PRIMES STEP senior group (Eric Chen, Adam Ge, Andrew Kalashnikov, Ella Kim, Evin Liang, Mira Lubashev, Matthew Qian, Rohith Raghavan, Benjamin Taycher, and Samuel Wang) studied the Conway-Ryba paper and decided to generalize it to Tribonacci numbers.
Just a reminder. The Tribonacci sequence starts as 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, and continues so that any next term is the sum of the three previous terms. For example, the next term after 44 is 81.
Now we need an analog of the Wythoff array for Tribonacci numbers. My readers might by now guess why I chose the above definition of the Wythoff array. Yes, this definition is perfect for generalizing to Tribonacci numbers.
We start by defining the Tribonacci base. We can represent every integer uniquely as a sum of distinct Tribonacci numbers on the condition that there are no three consecutive Tribonacci numbers in the sum. This is called a Tribonacci representation. We can express it with zeros and ones, and there will never be three ones in a row. For example, 16 can be expressed as a sum of Tribonacci numbers in the following way: 16 = 13 + 2 + 1. Thus, its Tribonacci representation is 10011.
We can define a Tribonacci successor, similarly to the Fibonacci successor, by adding a zero in the Tribonacci representation. For example, the Tribonacci successor of 16 has to have the Tribonacci representation 100110 and is equal to 24 + 4 + 2 = 30.
Now, we define the Tribonacci array similarly to the Wythoff array. The first row of the Tribonacci array consists of distinct Tribonacci numbers in order. The first column consists of integers whose Tribonacci representations end in 1. The number in the nth column is a Tribonacci successor of the number to its left.
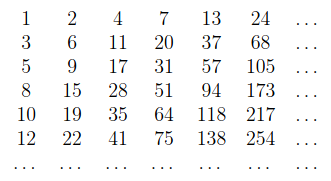
We found many cool properties of the Tribonacci array. They are in our paper, Generalizing the Wythoff Array and other Fibonacci Facts to Tribonacci Numbers, posted on the arXiv. Let me give you three examples of these awesome properties.
- Consider any integer sequence such that the next term is a sum of the three previous terms. We call such sequences Tribonacci-like. One of the cool properties is that, in some sense, the Tribonacci array contains all positive Tribonacci-like sequences. More formally, if a Tribonacci-like sequence has three consecutive positive terms, then the tail of such a sequence has to appear in the Tribonacci array as one of the rows.
- It follows that multiples of any row in the Tribonacci array have to appear in the array. An awesome fact is that they appear in order.
- Moreover, when all the numbers of a row are divisible by n, the row number minus 1 is also divisible by n.
It is easy to extend the Tribonacci array to the left, but this extension doesn’t have the same nice properties as the extension of the Wythoff array. So finding an Empire State Building, or any other building, in the Tribonacci array is futile.
Share: