Polyomino Cutting Solution
I recently posted the following polyomino puzzle, and my readers are asking for a solution.
Puzzle. You are given a 5-by-7 rectangle with two corners cut out: A 1-by-1 tile is cut from the bottom left corner, and a 1-by-2 tile is cut out of the top right corner, as pictured. The task is to cut the resulting shape into two congruent polyominoes.
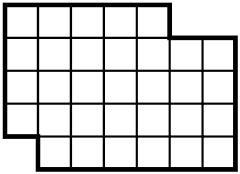
If a solution exists, there should be a transformation between the two congruent pieces. We can exclude a reflection and a central symmetry, as the union of the two shapes would have to be symmetric. We can exclude a translation: I leave it to the readers to explain why. What is left is a rotation or a glide. Let me remind you that a glide is composed of a reflection with respect to a line and a translation parallel to the line.
People often forget about glides, so this puzzle might be cool precisely because it is about glides. This is where we should start. We can safely assume that the top left corner belongs to piece A and, after the glide transformation, becomes the bottom right corner of piece B. It is also clear that the reflection line is parallel to the grid diagonals.
Then, we can start drawing the shapes. Piece A’s border starts from the top left corner and moves four squares down, then one square to the right, then one square down. Thus, piece B’s border starts at the bottom right corner and continues four squares to the left, then one square up, then one square to the left. In doing so, we reveal how the border of piece A continues. Thus, we can proceed in this manner to get the answer pictured below.

Share:
lvps1000vm:
If someone wants more of it, the Math+ calendar from 2019 has four more polyomino cuts like this one:
30 November 2023, 8:30 amhttps://www.mathekalender.de/wp/wp-content/uploads/2021/07/MK-2019-Solutions-en.pdf
(Challenge 24-Sawmill on page 140)
Gregory:
The polyomino puzzle is quite interesting I thought.
4 February 2024, 7:12 am