A Quadrilateral in a Rectangle Solution
I recently posted A Quadrilateral in a Rectangle puzzle.
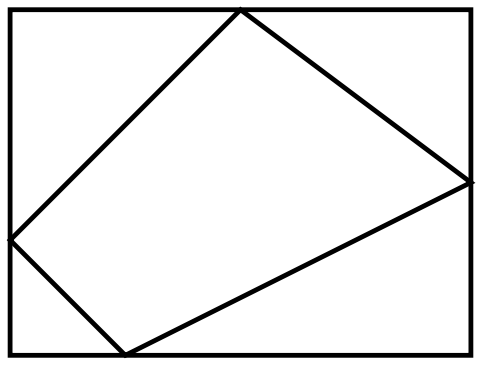
Puzzle. A convex quadrilateral is inscribed in a rectangle with exactly one quadrilateral’s vertex on each side of the rectangle. Prove that the area of the rectangle is twice the area of the quadrilateral if and only if a diagonal of the quadrilateral is parallel to two parallel sides of the rectangle.
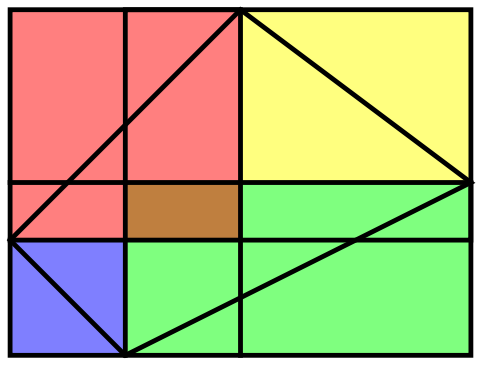
Now it is time for a solution where I use the sample rectangle pictured below. We draw lines parallel to the sides of the rectangle from every vertex of the quadrilateral. Now, we can find four pairs of congruent triangles where one triangle is inside the quadrilateral and the other is outside. In the picture below, the pairs are colored the same color. We see that green and red rectangles overlap, creating a brown rectangle. The fact that they overlap means that the quadrilateral’s area is less than half of the rectangle’s area.
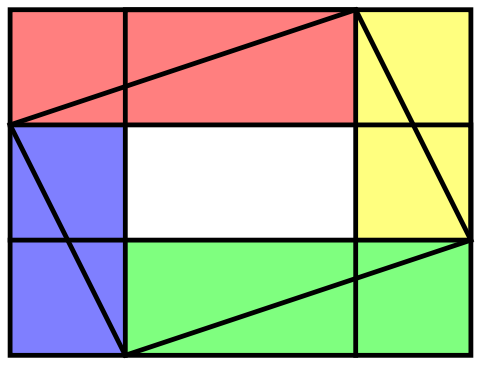
It could go the other way, as the next picture shows. Here, the quadrilateral’s area is more than half of the rectangle’s area. In this case, we have an “underlap” as opposed to an overlap.
Therefore, the quadrilateral’s area is exactly half of the rectangle’s if and only if there is no overlap/underlap, implying that the thickness of the overlap/underlap rectangle is zero. This means that one of the diagonals of the quadrilateral has to be parallel to two sides of the rectangle.
Share:
Carnival 170: A Plethora of Playful Math – Denise Gaskins' Let's Play Math:
[…] Tanya Khovanova poses a nice Quadrilateral in a Rectangle puzzle (solution here). […]
11 January 2024, 5:16 pmIvanGrozny:
Intriguing geometric puzzle, beautifully explained with clear visuals.
31 January 2024, 3:43 am