Polyomino Cutting
What’s a polyomino? A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. Here, we have a puzzle about a polyomino that is almost a rectangle.
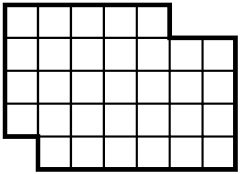
Puzzle. You are given a 5-by-7 rectangle with two corners cut out: A 1-by-1 tile is cut from the bottom left corner, and a 1-by-2 tile is cut out of the top right corner, as in the picture. The task is to cut the resulting shape into two congruent polyominoes.
Share:
Ivan:
Let us imagine this shape as 2 intersecting quadrilaterals: upper left green quadrilateral A (4 rows, 5 columns) and lower right blue quadrilateral B (4 rows, 6 columns). Their intersection is the yellow quadrilateral C (3 rows, 4 columns), which can be divided into two congruent polyominoes. In order to divide the whole shape into two congruent polyominoes, the green and blue remainders have to be added to the respective halves of the yellow quadrilateral in a symmetric fashion, which is impossible.
4 November 2023, 6:52 amLazar Ilic:
XXXXO
6 November 2023, 8:32 amXXXXOOO
XXOXXOO
XXOOOOO
XXOOOO
Mauro:
What is the definition of a cut? One connected path? Can it be along the edges?
6 November 2023, 9:23 amtanyakh:
Mauro, the cut should be along the grid.
6 November 2023, 12:24 pmMurat:
Does it have a solution?
17 November 2023, 11:21 pmJBL:
Is there a polyomino for which it is only possible to divide it into two congruent unions of squares if the pieces are not connected?
19 November 2023, 9:49 amTanya Khovanova's Math Blog » Blog Archive » Polyomino Cutting Solution:
[…] recently posted the following polyomino puzzle, and my readers are asking for a […]
29 November 2023, 8:27 pmAli Mohammadinia:
■■□□□□
30 November 2023, 9:16 am■■□□□□□
■■□■■□□
■■■■□□□
■■■■□