Geometric Transformations
In my days of competing in math, I met guys who could solve any geometry problem by using coordinates: first they would assign variables to represent coordinates of different points, then they would write and solve a set of equations. It seemed so boring. Besides, this approach doesn’t provide us with any new insight into geometry.
I find geometric solutions to geometry problems much more interesting than algebraic solutions. The geometric solutions that use geometric transformations are often the shortest and the most beautiful.
I.M. Yaglom wrote a great trilogy called The Geometric Transformations. The first book of this trilogy
I think geometry is the weakest link for the USA math team. So we have to borrow the best geometry books from other countries. This trilogy was translated from Russian and Russians are known for their strong tradition of excellence in teaching geometry.
Below you can find sample problems from Geometric Transformations 1
I.M. Yaglom wrote a great trilogy called The Geometric Transformations. The first book of this trilogy discusses translations, rotations and reflections. The second one — looks at similarity transformations, and the third one talks about affine and projective transformations. A lot of beautiful problems with their solutions are scattered throughout these books. They include all my favorite problems related to transformations.
I think geometry is the weakest link for the USA math team. So we have to borrow the best geometry books from other countries. This trilogy was translated from Russian and Russians are known for their strong tradition of excellence in teaching geometry.
Below you can find sample problems from Geometric Transformations 1, Geometric Transformations 2 and Geometric Transformations 3 — not necessarily in this order.
Problem 1. Let A be a point outside a circle S. Using only a straightedge, draw the tangents from A to S.
Problem 2. At what point should a bridge be built across a river separating two towns A and B (see figure) in order that the path connecting the towns be as short as possible? The banks of the river are assumed to be parallel straight lines, and the bridge is assumed to be perpendicular to the river.
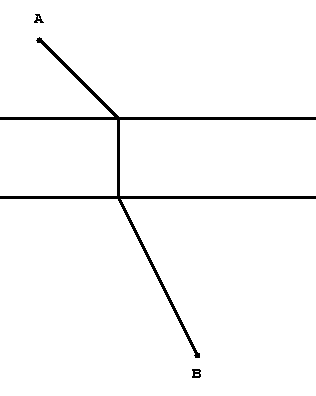
Share:Problem 3. Suppose you have two lines drawn on a piece of paper. The intersection point A of the two lines is unreachable: it is outside the paper. Using a ruler and a compass, draw a line through a given point M such that, were the paper bigger, point A would belong to the continuation of the line.
Jonathan:
For #1, can my straightedge have 2 parallel sides?
17 October 2009, 12:09 pmJonathan:
For #2, drop a perpendicular from A through C, on the near bank, continuing to D, on the far bank. Find E on ACD such that AE = CD…
17 October 2009, 12:15 pmJonathan:
For #3 are you certain a ruler is needed? I think I can do it with a straightedge.
17 October 2009, 12:21 pmTanya Khovanova:
Jonathan, Sorry, I am Russian, I can confuse a rule and a straightedge. What’s the difference? We need a thing that allows us to draw a line through two given points – that’s all. And I do not think that you need two parallel sides.
17 October 2009, 12:30 pmJonathan:
Straightedge is a stick used to draw lines. It has one edge, and should be without markings (ie, cannot be used to measure), though we often use a marked off stick and just pretend the markings are not there.
In regular English, a ruler is a stick used to measure length. It has a straight edge, and it has markings, eg in eighths of inches.
For construction only, a ruler is a stick with two parallel sides. It should not be marked, or the markings should be ignored. Many good constructions can be performed with only a ruler (no compass).
BTW, I found all three volumes on my shelf. I will propose to a friend that we read and solve together – a little joint study to keep the brains nimble. Thanks for recommending.
17 October 2009, 1:08 pmmisha:
About #2: I guess it is assumed that the bridge is perpendicular to the riverbank.
17 October 2009, 11:38 pmKevin:
For #2: Let’s assume that point A is located at (X_A, Y_A), point B at (X_B, and Y_B), and the river between the lines Y=Z_1 and Y=Z_2. If we build the bridge along the line X=Z_0, we can then compute the sum of the distances directly as…
Instead, how about moving point A down by a distance equal to the width of the river and perpendicular to it? The shortest path is now a straight line, and we draw the bridge upwards from where the line intersects the bottom of the river.
21 October 2009, 10:05 pmJonathan:
We now have 2 solutions to #3… I am proud that I found anything (construction is not a strength), but my friend found something elegant, relying on the 3 altitudes of a triangle being concurrent (intersecting in a single point).
I found 2 copies of Volume 1 (actually, one was without volume # at all, must have been the very first printing), and we are planning to read and discuss. Thanks for pointing us to Yaglom – he looks fun.
22 October 2009, 7:16 amnot russian, but...:
My memory of Yaglom’s books is that some of the problems were unreasonably hard because of the “elementary” viewpoint that he takes. This was true also of the Challenging Problems volumes that he wrote with his brother. Still, the books are classics in many ways.
27 October 2009, 2:23 amMore Puzzle Extension: Expressing n as the sum of consecutive integers « JD2718:
[…] New Mathematical Library series (mid-1960’s) which includes about 30 titles, including Yaglom’s 3-part Geometry, which wonderful puzzler Tanya Khovanova blogged about last […]
14 November 2009, 12:55 pmBoris:
For problem #3, you don’t even need a compass. A straightedge — that is, something that can draw a line connecting two points — is all that is needed. This follows from Pappus’s theorem.
29 November 2009, 2:57 pmandre:
Problem 2.
Assume the river’s width is 0. Then put a straight line between A and B. Restore river’s width. Make bridge at the intersection of the AB and the zero-width river.
Экскьюз май френч.
11 January 2010, 11:30 amMichael:
I cannot figure out problem 3 for the life of me. I’m trying to use pappus’s theorem but cant seem to get it. Any hints?
21 July 2010, 12:13 amAlex:
Michael, did you ever figure this out? I got asked this question in a math lecture. They used an example of a river bank where the intersection is behind a wall. Help would be amazing
21 March 2012, 11:25 pm