Tanya Khovanova's Math Blog

I had a distant relative Alla, who was brought up by a single mother, who died in a car crash when the girl was in her early teens. Alla was becoming a sweet and pleasant teenager; she was taken in by her aunt after the accident. Very soon the aunt started complaining that Alla was turning into a cheater and a thief. The aunt found a therapist for Alla, who explained that Alla was stealing for a reason. Because the world had unfairly stolen her mother, Alla felt entitled to compensation in the form of jewelry, money, and other luxuries.

I was reminded of Alla’s story when I was reading The (Honest) Truth About Dishonesty: How We Lie to Everyone—Especially Ourselves by Dan Ariely. Ariely discusses a wide range of reasons why honest people cheat. But to me he neglects to look at the most prominent reason. Often honest people cheat when they feel justified and entitled to do so.

One of Ariely’s experiments went like this. One group was asked to write a text avoiding letters x and z. The other group was asked to write a text avoiding letters a and n. The second task is way more difficult and requires more energy. After the tasks were completed the participants were given a test in which they had a chance to cheat. For this experiment, the participants were compensated financially according to the number of questions they solved. Not surprisingly, the second group cheated more. The book concludes that when people are tired, their guard goes down and they cheat more. I do not argue with this conclusion, but I think another reason also contributes to cheating. Have you ever tried to write a text without using the letters a and n? I did:

I should try it here. But this is so difficult. I give up.

My son, Alexey, was way better than me:

First, God brought forth the sky with the world. The world existed without form. Gloom covered the deep. The Spirit of God hovered over the fluids. Quoth God: let there be light. Thus light existed.

Fun as it is, this is cruel and unusual punishment. The request is more difficult than most people expect at an experiment. It could be that participants cheated not only because their capacity for honesty was depleted, but because they felt entitled to more money because the challenge was so difficult.

In another experiment, the participants received a high-fashion brand of sunglasses before the test. Some of them were told that the sunglasses were a cheap imitation of the luxury brand (when they really were not). This group cheated more than the group who thought that they got a real thing. The book concludes that wearing fake sunglasses makes people feel that they themselves are fake and so they care less about their honor. Unfortunately, the book doesn’t explain in detail what was actually promised. It looks like the participants were promised high-fashion sunglasses. In this case, the fake group would have felt deceived and might have felt more justified to cheat.

Dear Dan Ariely: May I suggest the following experiment. Invite people and promise them some money for a 15-minute task. Pay them the promised minimum and give them a test through which they can earn more. Construct it so that they can earn a lot more if they cheat. Then make the non-control group wait for half an hour. If I were in this group, I would have felt that I am owed for the total of 45 minutes—three times more than what I was promised. I do not know if I would cheat or just leave, but I wouldn’t be surprised that in this group people would cheat more than in the control group.

I received a book Really Big Numbers by Richard Schwartz for review. I was supposed to write the review a long time ago, but I’ve been procrastinating. Usually, if I like a book, I write a review very fast. If I hate a book, I do not write a review at all. With this book I developed a love-hate relationship.

Let me start with love. I enjoyed reading the first 80 pages. The pictures are great, and some explanations are very well thought out. Plus, I haven’t thought much about really big numbers, so the book helped me understand them. I was impressed with how this book treats very difficult ideas with simple explanations and illuminating images. I was captivated by it.

Now to hate. I had two problems with this book: one pedagogical and the other mathematical.

The pedagogical issue. The beginning of the book is suitable for small children. Most of the book is suitable for advanced middle-schoolers who like mathematics. The last part is very advanced. Is it a good idea to show children a book that looks like a children’s book, but which soon becomes totally out of their reach? Richard Schwartz understands it and says many times that pieces of this book might be read several years apart. Several years? What child is ready to wait several years to finish a book? How would children feel about the book and about numbers when no matter how hard they try, they cannot understand the end of the book?

As a reviewer, I can’t recommend the full book for kids who are not ready to grasp the notion of the Ackermann function or arrow notation. Even if the child is capable of understanding these ideas, there are mathematical issues that would prevent me from recommending it.

The mathematical issue. Let me start by explaining the notion of plex. We call an n-plex a number that is equal to 10ⁿ. For example, 2-plex means 10² which is 100, and 10-plex means 10¹⁰. The fun part starts when we plex plexes. The number n-plexplex means 10 to the power n-plex which is 10⁽¹⁰¹⁰⁾. We can continue plexing: n-plexplexplex means 10 to the power n-plexplex. When you are hunting for really big numbers, it is easier to write the number of plexes rather than writing plexes after plexes. Richard Schwartz introduces the following notation to help visualize the whole thing. He puts numbers in a square. Number n in a square means 1-plexed n times. For example, 2 inside a square means 10¹⁰. Ten inside a square is 1-plexplexplexplexplexplexplexplexplexplex.

We can start nesting squares. For example, 2 inside a square means 1-plex-plex or 10¹⁰. Let’s add a square around it: 2 inside two squares means 10¹⁰ inside a square, which equals 1 plexed 10¹⁰ times. To denote 10 nested in n squares Richard Schwartz uses the next symbol: n inside a pentagon. For example, 1 inside a pentagon is 10 inside a square. I wrote this number in the previous paragraph: it is 1-plexplexplexplexplexplexplexplexplexplex. Similarly, n inside a hexagon means 10 inside n nested pentagons. We can continue this forever: n inside a k-gon is 10 inside k nested (k-1)-gons.

What bothers me is why a square? Why not a triangle? If we adopt this scheme, what is the meaning of a number in a triangle? Let’s try to unravel this. Following Richard Schwartz’s notation we get that n inside a square is the same as 10 inside n nested triangles. What do we do n times with 10 to get to 1 plexed n times? 1-plexed n times is 10 plexed n-1 times. There is a disconnect in notation here. For example, 10 in two nested triangles should mean 2 inside a square that is 10¹⁰. 10 inside one triangle should mean 1 inside a square which is 10. This doesn’t make any sense.

I started googling around and discovered the Steinhaus–Moser notation. In this notation a number n in a triangle means nⁿ. A number n in a square means the number n inside n nested triangles. A number n in a pentagon means the number n inside n nested squares. And so on. This makes total sense to me. If we move down the number of sides, we can say that the number n inside a 2-gon means n times n and the number n inside a 1-gon means n. This is perfect.

Schwartz changed the existing notation in two places. First he made everything about 10. This might not be such a bad idea except his 10 inside a square doesn’t equal 10 inside a square in Steinhaus–Moser notation. In Steinhaus–Moser notation 10 inside a square means 10 plexed 10 times. The author removed one of the plexes. He made 10 inside the square to mean 1 plexed 10 times, and as a result it stopped working.

Even though the first 83 pages are delightful and the pictures are terrific, the notation doesn’t work. What a pity.

Some of my friends collect volumes of The Best Writing on Mathematics published by Princeton University Press. The first annual volume appeared in 2010. In 2014, one of my papers, Conway’s Wizards, was chosen to be included in the volume The Best Writing on Mathematics 2014.

All my life I have hated writing. My worst grades in high school were for writing. I couldn’t write in Russian, and I was sure I would never be able to write in English. I was mistaken. I am a better writer than I gave myself credit for being.

Writing in English is easier for me than writing in Russian because when I make a mistake, I have an excuse. As my written English gets better and better, maybe one day I’ll get the courage to try writing in Russian.

I would like to use this opportunity to thank Sue Katz, my friend, English teacher, and editor. Sue edits most of my blog essays. Originally I wrote about Conway’s wizards on my blog. When I had three essays on the subject I combined them into a paper. Sue edited the essays and the paper. I am honored to be included in this respected volume and I want to share this honor with Sue.

I love making math questions out of the movies. Here is a Mission Impossible III question.

Tom Cruise is cute. He plays Ethan Hunt in Mission Impossible movies. In Mission Impossible III he needs to steal the Rabbit’s Foot from a secure skyscraper in Shanghai. He arrives in Shanghai and studies the skyscraper looking out his window. He decides to break in through the roof. And the way to get to the roof is to use a rope and swing across from another, even taller, skyscraper. 1:21 minutes into the movie, Ethan Hunt calculates the length of the rope he will need by using the projection of a skyline on his window, as seen on the first picture.

Explain why the projection is not enough to calculate the length of the rope. What other data does he need for that? Ethan Hunt does request extra data. But he makes one mistake. He uses his pencil as a compass to draw the end of the rope curve, as seen on the second picture. Explain what his mistake is.

I received the book Taking Sudoku Seriously by by Jason Rosenhouse and Laura Taalman for review and put it aside to collect some dust. You see, I have solved too many Sudokus in my life. The idea of solving another one made me barf. Besides, I thought I knew all there is to know about the mathematics of Sudoku.

One day out of politeness or guilt I opened the book — and couldn’t stop reading.

The book is written for people who like Sudoku, but hate math. This is so strange. Sudoku is math. People who are good at Sudoku are good at math, or at least they are supposed to be. It seems that math education in the United States is so bad that people who were born to be good at math and to like math, hate it instead. So the goal of the book is to establish a bridge from Sudoku to math. And the book does a superb job of it.

This well-written book moves from puzzles to discussions in such a natural way that math becomes a continuation of puzzles.

Taking Sudoku Seriously covers a lot of fun material: methods to solve Sudoku, how to count the number of different Sudoku puzzles, and how to find the smallest number of clues that are needed for a unique puzzle. The book travels into the neighboring area of Latin and Greco-Latin squares. While discussing all those fun things it covers groups, symmetries, number theory, graph theory (including book thickness) and more.

I am not the target audience for this book, because I do not need convincing that math is fun. The best part for me was the hundred puzzles. Only a portion of them were standard Sudoku puzzles — and I skipped those. The others were either Sudoku with a twist or plain math puzzles.

The puzzles are all very different and I was so excited by them, that I went ahead and solved them, and caught up with reading the text later. And I enjoyed both: reading and solving.

Here is puzzle 91 from the book. Fill in the grid so that every row, column, and block contains 1-9 exactly once. In addition, each worm must contain entries that increase from tail to head. For blue worms you must figure out yourself which end is the head.

My American friends often ask me for insights into why Grigory Perelman refused the one million dollar Clay prize for his proof of the Poincaré conjecture. They are right to ask me: my life experience was very similar to Perelman’s.

I went to a high school for children gifted in math. I was extremely successful in competitions. I got my gold medal at IMO and went to college without entrance exams. I received my undergraduate and graduate degrees in one of the best math academic centers in Soviet Russia. Perelman traveled a similar path.

Without ever having met Perelman, I can suggest two explanations of why he might reject the money.

First explanation. To have it publicly known that you have suddenly come into money is very dangerous in Russia. Perelman’s life expectancy would have dropped immediately after accepting the million dollars. Russians that have tons of money either hide their wealth or build steel doors way before they make their first million. In addition to being a life hazard, money attracts a lot of bother. He would have been chased by all types of acquaintances asking for help or suggesting marriage proposals.

Second explanation. We grew up in a communist culture where money was scorned and math was idolized. The goal of research was research. Proving the conjecture was the prize itself. In his mind, receiving the award money might diminish the value of what he did. I understand this way of thinking, but I am personally too practical to follow such feelings and would accept the prize.

My first explanation has a flaw. Though valid, it doesn’t explain why he rejected the Fields medal. So I reached for the book abour Perelman, Perfect Rigor: A Genius and the Mathematical Breakthrough of the Century by Masha Gessen. I like Gessen’s explanation of why he rejected the Fields medal:

His objection to the Fields Medal, though never stated as clearly, seemed to have been twofold: first: he no longer considered himself a mathematician and hence could not accept a price intended for the encouragement of midcareer researchers; and second, he wanted no part of ICM, with all the attendant publicity, speeches, ceremony, and king of Spain.

The reasons are specifically related to the medal, so the Clay prize rejection might not be connected to the medal rejection. This argument slightly rehabilitates my first explanation.

I liked the book. It is a tremendous undertaking — writing about a person who doesn’t want to talk to anyone. After reading it, I have one more possible explanation of his refusal of the prize.

Perelman is a loner. One of the closest people to him was his math Olympiad coach. The coaches tend to understand the solutions on the spot, mostly because they already know them. If in his mind Perelman expected all mathematicians to be like his coach, then he might have expected a parade in his honor the day after he solved the conjecture. Instead, he got silence and attempts to steal the prize from him.

Can you imagine doing the century’s best math work without receiving congratulations for many years? The majority of mathematicians waited for the judgment of the experts, as did Perelman. The experts were busy and much slower than Perelman expected. The conjecture was extremely difficult, and it was a high-profile situation — after all, $1 million was attached to its solution. So the experts were very cautious in their pronouncements.

Finally, instead of congratulating Grigory, they said that the proof seemed to be correct and that they had not yet found any mistakes. If like Perelman, I was certain of my proof, I would have found this a painfully under-whelming conclusion.

Perelman expected to feel proud, but instead he probably felt unappreciated and attacked. Instead of the parade he may have hoped for, he had to wait for a long time, only to face disappointment and frustration. This reminds me of an old joke:

A genie is trapped in a lantern at the bottom of the sea. He vows, “I will give one million dollars to the person who frees me.” One thousand years pass. He changes his vow, “I will give any amount of money to the one who frees me.” Another thousand years pass. He ups the ante, “I will give any amount of money and two more wishes to the person who frees me.” Another thousand years pass. He promises, “I will kill the one who frees me.”

Third explanation. Perelman was profoundly disappointed in the math community. Unlike the genie, Perelman didn’t want to kill anyone, but he did want to express his disillusionment. Perhaps that is why he rejected a million dollars.

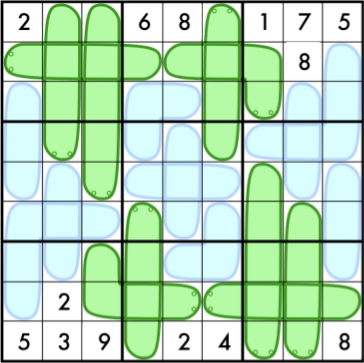
Do you like challenging puzzles? Are you tired of sudoku? Here’s your chance to try your hand at puzzles that are designed for world puzzle championships.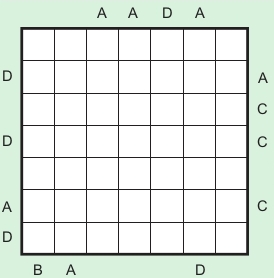

I’ve already done the homework for you — and it turned out to be more complicated than I anticipated. The world puzzle federation has a website, but unfortunately they are lazy or secretive. It is difficult to find puzzles there. A few puzzles are available in the World Puzzle Federation Newsletters.

Since I am stubborn, I spent a lot of time looking for championship puzzles. I found them in books. Here is the list I compiled so far. If you too are interested in high-level puzzles, this ought to make your search a lot easier. The book titles are confusing, so I added a description of what’s in them.

• Games Magazine Presents Brain Twisters from the First World Puzzle Championships — Warm-up puzzles, US/Canada Qualifying test, First World Championship, Foreign team puzzles.
• Games Magazine Presents Brain Twisters from the World Puzzle Championships, Volume 2 — US/Canada Qualifying test, Second World Puzzle Championship, Third World Puzzle Championship.
• Games Magazine Presents Brain Twisters from the World Puzzle Championships, Volume 3 — Fourth World Puzzle Championship, Fifth World Puzzle Championship.
• World Puzzle Championships Omnibus, Volume 1 — Contains World-Class Puzzles from the World Puzzle Championships Volumes 1-3 below.
• World-Class Puzzles from the World Puzzle Championships, Volume 1 — Sixth World Puzzle Championship and Seventh World Puzzle Championship.
• World-Class Puzzles from the World Puzzle Championships, Volume 2 — 1999 Qualifying test, Eighth World Puzzle Championship.
• The New York Times Sunday Crossword Omnibus, Volume 3 — 2000 Qualifying test, Ninth World Puzzle Championship.
• World-Class Puzzles from the World Puzzle Championships, Volume 4 — 2001 Qualifying test, Tenth World Puzzle Championship.
• World-Class Puzzles from the World Puzzle Championships, Volume 5 — 2002 Qualifying test, Eleventh World Puzzle Championship.
• Random House World-Class Puzzles — 2002 Qualifying test, Twelfth World Puzzle Championship. (The year for the qualifying test is probably a typo as puzzles differ from the qualifying test in the previous book,)

One of my favorite puzzle types is Easy as ABC. You have to fill one of A, B, C, and D in each row and column. The letters outside the grid indicate which letter you see first from that direction. Here is one from the 2011 newsletter:

Two girls. One is older and more experienced. The other is younger and more naive. Which of these two girls will the unnamed male narrator choose? What a great plot for a math book.

I am talking about Hiroshi Yuki’s book Math Girls. The plot allows the author to discuss math on different levels. Miruka’s math is more advanced and mysterious. Tetra’s math is simpler and more transparent.

The book starts discussing sequences and patterns. Can you guess the pattern behind the sequence: 1, 2, 3, 4, 6, 9, 8, 12, 18, 27, …? Can you explain how the beginning of this sequence might be very deceptive?

For the answer, you can read the book, which also discusses tons of fun topics: prime numbers, sum of divisors, absolute values, rotations and oscillations, De Moivre’s formula, generating functions, arithmetic and geometric means, differential and difference operators, Catalan numbers, infinite series, harmonic numbers, zeta function, Taylor series, partitions, and more.

I usually do not like math fiction, but this is more math than fiction. It’s quite superior to most other math books I’ve read, for it shows the unity of mathematics. It allows the readers to discover connections among different parts of mathematics, and it accomplishes this in a very thrilling way. Frankly, more thrilling than the romantic sections.

The fictional element brings an additional value to the book. The author uses dialogue to discuss points that are usually skipped in regular text books. The two girls give the narrator an opportunity to explore math on different levels: to talk about heavy stuff with Miruka and to provide explanations with Tetra.

I expected to be more interested in the sections dealing with advanced math. But the book is so well-written that the simpler things were a lot of fun, too. For example, I never before noticed that the column notation for n choose k is exactly the same as for a 2d vector with coordinates n and k. And I will never ever shout “zero” because the exclamation makes it “one”.

I have already written about how American math competition are illogically structured, for the early rounds do not prepare students for the later rounds. The first time mathletes encounter proofs is in the third level, USAMO. How can they prepare for problems with proofs? My suggestion is to look East. All rounds of Russian math Olympiads — from the local to the regional to the national — are structured in the same way: they have a few problems that require proofs. This is similar to the USAMO. At the national All-Russian Olympiad, the difficulty level is the same as USAMO, while the regionals are easier. That makes the problems from the regionals an excellent way to practice for the USAMO. The best regional Olympiad in Russia is the Moscow Olympiad. Here is the problem from the 1995 Moscow Olympiad:

We start with four identical right triangles. In one move we can cut one of the triangles along the altitude perpendicular to the hypotenuse into two triangles. Prove that, after any number of moves, there are two identical triangles among the whole lot.

This style of problems is very different from those you find in the AMC and the AIME. The answer is not a number; rather, the problem requires proofs and inventiveness, and guessing cannot help.

Here is another problem from the 2002 Olympiad. In this particular case, the problem cannot be adapted for multiple choice:

The tangents of a triangle’s angles are positive integers. What are possible values for these tangents?

The problems are taken from two books: Moscow Mathematical Olympiads, 1993-1999, and Moscow Mathematical Olympiads, 2000-2005. I love these books and the problems they present from past Moscow Olympiads. The solutions are nicely written and the books often contain alternative solutions, extended discussion, and interesting remarks. In addition, some problems are indexed by topics, which is very useful for teachers like me. But the best thing about these books are the problems themselves. Look at the following gem from 2004, which can be used as a magic trick or an idea for a research paper:

A deck of 36 playing cards (four suits of nine cards each) lies in front of a psychic with their faces down. The psychic names the suit of the upper card; after that the card is turned over and shown to him. Then the psychic names the suit of the next card, and so on. The psychic’s goal is to guess the suit correctly as many times as possible.
The backs of the cards are asymmetric, so each card can be placed in the deck in two ways, and the psychic can see which way the top card is oriented. The psychic’s assistant knows the order of the cards in the deck; he is not allowed to change the order, but he may orient any card in either of the two ways.
Is it possible for the psychic to make arrangements with his assistant in advance, before the latter learns the order of the cards, so as to ensure that the suits of at least (a) 19 cards, (b) 23 cards will be guessed correctly?
If you devise a guessing strategy for another number of cards greater than 19, explain that too.

My co-author Konstantin Knop wrote a charming book, Weighings and Algorithms: from Puzzles to Problems. The book contains more than one hundred problems. Here are a couple of my favorites that I translated for you:

There is one gold medal, three silver medals and five bronze medals. It is known that one of the medals is fake and weighs less than the corresponding genuine one. Real medals made of the same metal weigh the same and from different metals do not. How can you use a balance scale to find the fake medal in two weighings?

There are 15 coins, out of which not more than seven are fake. All genuine coins weigh the same. Fake coins might not weigh the same, but they differ in weight from genuine coins. Can you find one genuine coin using a balance scale 14 times? Can you do it using fewer weighings?

You might get the impression that the latter problem depends on two parameters. Think about it: It is necessary that the majority of the coins are genuine in order to be able to solve the problem. In fact, the number of weighings depends on just one parameter: the total number of coins. Denote a(n) the optimal number of weighings needed to find a genuine coin out of n coins, where more than half of the coins are genuine. Can you calculate this sequence?

Hint. I can prove that a(n) ≤ A011371(n-1); that is, the optimal number of weighings doesn’t exceed n − 1 − (number of ones in the binary expansion of n−1).