In December 2022, I wrote a blog post Uncrossed Knight’s Tours about Derek Kisman’s amazing achievement of calculating the largest uncrossed knight’s tours on rectangular chessboards on sizes M-by-N, where M is small, and N can be very very large.
The data showed some asymptotic periodicity, and I wondered how to prove it mathematically. I didn’t realize that Derek already proved it. In my ignorance of programming, I assumed that programs just spewed out the data and didn’t think they could prove anything. I was wrong. It appears that no other proof is needed. Derek tried to explain the details to me using the terminology of dynamic programming, but I am not sure I can reproduce it here.
Let’s recall the problem. Consider an M-by-N chessboard and a knight that moves according to standard chess rules: jumping one square in one direction and two squares in an orthogonal direction. The knight must visit as many squares as possible, without repeats, and then return to its starting square. In addition, the knight may never cross its own path. If you imagine the knight’s path consisting of straight line segments connecting the centers of the squares it visits, these segments must form a simple polygon. To summarize, given M and N, we want to calculate the longest uncrossed knight’s tour length.
To be clear: the programs, their output data, proven answers, and images are by Derek Kisman. I am just a humble messenger showing my new appreciation of the power of a computational proof.
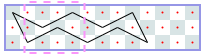
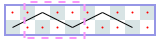
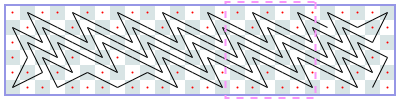
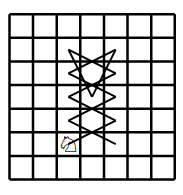
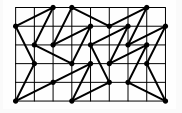
The image shows Derek’s solution for a 3-by-13 chessboard. There is a repeating 3-by-4 pattern marked by dashed lines. The same tour works for boards of lengths 10, 11, and 12. Thus, for chessboards of width 3 and length from 10 to 13 inclusive, the longest uncrossed knight’s tour is length 10. We can write the answers for 3-by-N chessboards as a sequence with index N, where -1 means the tour is impossible. The sequence starts with N = 1: -1, -1, -1, 4, 6, 6, 6, 6, 10, 10, 10, 10, 14, 14, ….
We can prove that this sequence is correct without programming. Suppose the tour starts in the leftmost column. If we start in the middle of the column, the whole tour ends as a rhombus and a tour of length 4, which, by the way, is the longest tour for N = 5. Thus, for a larger N, we have to start in a corner. From there, there are only two possible moves. We can see that the continuation is unique and that, asymptotically, we gain one step per extra column. That is, asymptotically, the length of the longest tour divided by N is 1.
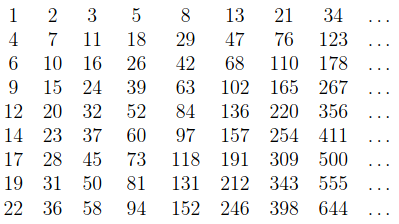
Derek uses an additional notation in the following sequence: each cycle is in brackets. Any two consecutive cycles differ by the same constant. So to continue the sequence indefinitely, it is enough to know the first two cycles.
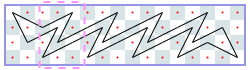
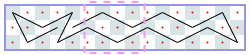
Closed tours: 3xN (asymptote 1): -1, -1, -1, -1, 4, [6, 6, 6, 6], [10, 10, 10, 10], …
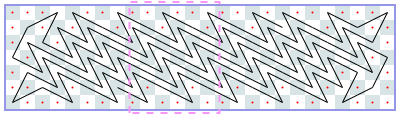
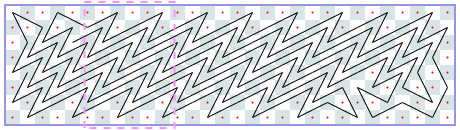
I continue with other examples Derek calculated:
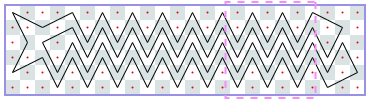
Closed tours: 4xN (asymptote 2): -1, -1, -1, [4], [6], …
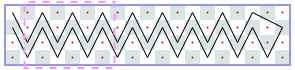
Closed tours: 5xN (asymptote 2 3/5): -1, -1, 4, 6, [8, 12, 14, 18, 20, 22, 24, 28, 30, 34], [34, 38, 40, 44, 46, 48, 50, 54, 56, 60], …
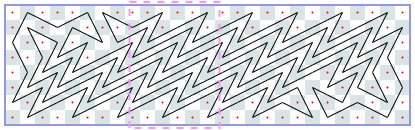
Closed tours: 6xN (asymptote 4): -1, -1, 6, 8, 12, 12, 18, 22, 24, 28, 32, 36, [38], [42], …
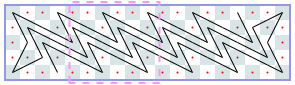
Closed tours: 7xN (asymptote 4 10/33): -1, -1, 6, 10, 14, 18, 24, 26, 32, 36, 42, 44, 48, 54, 58, 62, 66, 72, 74, 80, 84, 88, 94, 98, 100, 106, 112, 114, 118, 124, 128, 130, [136, 140, 144, 148, 154, 158, 162, 166, 170, 176, 180, 184, 188, 192, 196, 200, 204, 210, 214, 218, 222, 226, 232, 236, 240, 244, 248, 254, 256, 260, 266, 270, 274], [278, 282, 286, 290, 296, 300, 304, 308, 312, 318, 322, 326, 330, 334, 338, 342, 346, 352, 356, 360, 364, 368, 374, 378, 382, 386, 390, 396, 398, 402, 408, 412, 416], …
Closed tours: 8xN (asymptote 6): -1, -1, 6, 12, 18, 22, 26, 32, 36, 42, 46, 52, 58, [64, 70, 76, 80, 88, 92], [100, 106, 112, 116, 124, 128], …
Closed tours: 9xN (asymptote 6 6/29): -1, -1, 6, 14, 20, 24, 32, 36, 42, 50, 56, 60, 68, 74, 80, 86, 94, 98, 106, 114, 118, 126, 132, 136, [144, 150, 156, 162, 168, 174, 180, 186, 192, 200, 206, 212, 218, 224, 230, 236, 242, 250, 254, 262, 268, 274, 280, 286, 292, 300, 304, 312, 318, 324, 330, 336, 342, 348, 354, 360, 366, 372, 378, 386, 392, 398, 404, 410, 416, 422, 428, 436, 440, 448, 454, 460, 466, 474, 478, 486, 492, 498], [504, 510, 516, 522, 528, 534, 540, 546, 552, 560, 566, 572, 578, 584, 590, 596, 602, 610, 614, 622, 628, 634, 640, 646, 652, 660, 664, 672, 678, 684, 690, 696, 702, 708, 714, 720, 726, 732, 738, 746, 752, 758, 764, 770, 776, 782, 788, 796, 800, 808, 814, 820, 826, 834, 838, 846, 852, 858], …
Closed tours: 10xN (asymptote 8): -1, -1, 10, 16, 22, 28, 36, 42, 50, 54, 64, 70, 78, 84, 92, 100, [106], [114], … I do not have an image for this case.
As you might have noticed, for an even M, the asymptote equals M-2. The asymptote for an odd M is slightly greater than the asymptote for M-1.
Derek also calculated the longest open knight’s tours: the tours where the knight doesn’t have to return to its starting position.
Open tours: 2xN (asymptote 1/2): -1, -1, [2, 2], [3, 3], …
Open tours: 3xN (asymptote 1): -1, 2, 3, 5, 6, 7, [9], [10], …
Open tours: 4xN (asymptote 2): -1, 2, 5, [6], [8], …
Open tours: 5xN (asymptote 3): -1, 3, 6, 8, 11, 15, 17, 20, 23, 26, 29, [32, 35, 38, 41, 44, 46], [50, 53, 56, 59, 62, 64], …
Open tours: 6xN (asymptote 4): -1, 3, 7, 10, 15, 18, 22, 26, 30, 33, [36], [40], …
Open tours: 7xN (asymptote 5): -1, 4, 9, 12, 17, 22, 25, 31, 36, [40], [45], …
Open tours: 8xN (asymptote 6): -1, 4, 10, 14, 20, 26, 31, 36, 43, 48, 54, 60, [64], [70], …
Open tours: 9xN open (asymptote 7): -1, 5, 11, 16, 23, 30, 36, 43, 48, 56, 62, 68, 75, [82, 88, 94], [103, 109, 115], … I do not have an image for this case.
There are a lot of interesting new sequences in this essay that were very nontrivial to calculate. I hope someone adds them to the OEIS database.
Share: