Halving Lines
One of the 2012 PRIMES projects, suggested by Professor Jacob Fox, was about bounds on the number of halving lines. I worked on this project with Dai Yang.
Suppose there are n points in a general position on a plane, where n is an even number. A line through two given points is called a halving line if it divides the rest of n−2 points in half. The big question is to estimate the maximum number of halving lines.
Let us first resolve the small question: estimating the minimum number of halving lines. Let’s take one point from the set and start rotating a line through it. By a continuity argument you can immediately see that there should be a halving line through any point. Hence, the number of halving lines is at least n/2. If the point is on the convex hull of the set of points, then it is easy to see that it has exactly one halving line through it. Consequently, if the points are the vertices of a convex n-gon, then there are exactly n/2 halving lines. Thus, the minimum number of halving lines is n/2.
Finding the maximum number of halving lines is much more difficult. Previous works estimated the upper bound by O(n4/3) and the lower bound by O(ne√log n). I think that Professor Fox was attracted to this project because the bounds are very far from each other, and some recent progress was made by elementary methods.
Improving a long-standing bound is not a good starting point for a high school project. So after looking at the project we decided to change it in order to produce a simpler task. We decided to study the underlying graph of the configuration of points.
Suppose there is a configuration of n points on a plane, and we are interested in its halving lines. We associate a graph to this set of points. A vertex in the configuration corresponds to a vertex in the graph. The graph vertices are connected, if the corresponding vertices in the set have a halving line passing through them. So we decided to answer as many questions about the underlying graph as possible.
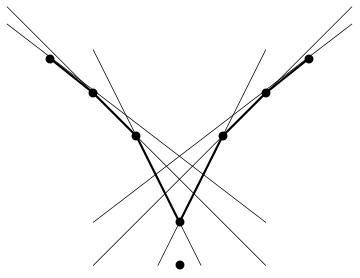
For example, how long can the longest path in the underlying graph be? As I mentioned, the points on the convex hull have exactly one halving line through them. Hence, we have at least three points of degree 1, making it impossible for a path to have length n. The picture below shows a configuration of eight points with a path of length seven. We generalized this construction to prove that there exists a configuration with a path of length n−1 for any n.
We also proved that:
- The largest cycle can have length n − 3.
- The largest clique is of the order O(√n).
- The degrees of two distinct vertices sum to at most n, if they are connected by an edge, and at most n − 2 otherwise.
After we proved all these theorems, we came back to the upper bound and improved it by a constant factor. Our paper is available at arXiv:1210.4959.
Share:
Leo B.:
I had a feeling I’ve seen similar point configurations before. Indeed, look at K8 here:
28 November 2012, 3:04 amhttps://mathworld.wolfram.com/RectilinearCrossingNumber.html
Javier Rodrigo:
I want to know what is the best current constant for the Dey’s upper bound: O(n k^(1/3))on the number of k-sets for sets of n points when n is an odd number and k=(n-3)/2.
25 January 2013, 8:31 pmThank you very much