Divisibility by 7 is a Walk on a Graph. II
by David Wilson
I was somewhat taken aback by the popularity of my earlier essay “Divisibility by 7 is a Walk on a Graph.” Tanya tells me it got a good number of hits. The graph in that article is rather crude, and takes a bit of care to use, because the arrows go off in random directions from each node. So taking a hint from a commenter on the first graph, I redrew the graph, sacrificing planarity in favor of ease of use. Specifically, I arranged the black arrows in a counterclockwise circle, which makes them easy to follow.
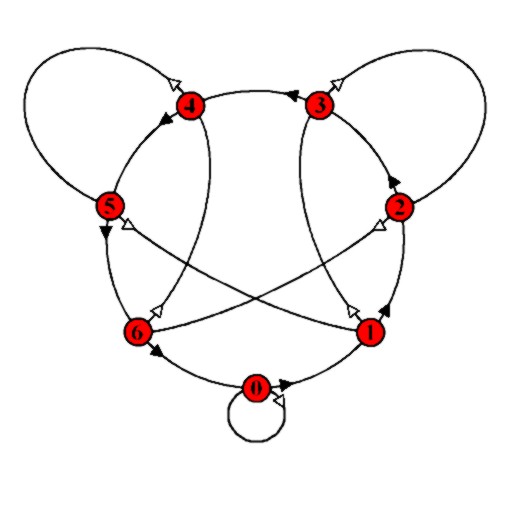 The graph is used in the same way as the first graph. To find the remainder on dividing a number by 7, start at node 0, for each digit D of the number, move along D black arrows (for digit 0 do not move at all), and as you pass from one digit to the next, move along a single white arrow.
The graph is used in the same way as the first graph. To find the remainder on dividing a number by 7, start at node 0, for each digit D of the number, move along D black arrows (for digit 0 do not move at all), and as you pass from one digit to the next, move along a single white arrow.
For example, let n = 325. Start at node 0, move along 3 black arrows (to node 3), then 1 white arrow (to node 2), then 2 black arrows (to node 4), then 1 white arrow (to node 5), and finally 5 black arrows (to node 3). Finishing at node 3 shows that the remainder on dividing 325 by 7 is 3.
I fancy it to be a little animal face.
riamu:
awesomecats
14 August 2010, 7:34 amAnton Sherwood:
In 1995 I got interested in enumerating fullerene topologies: that is, how many closed surfaces can be made from pentagons and hexagons meeting in threes? I found a plastic kit to model them, which helped me see the symmetries. I found a bunch of forms that looked like reptile heads, and a few that looked like turtles.
30 August 2010, 12:21 amDivisibility by 7 is a Walk on a Graph. II | programmingmeetsmath:
[…] Divisibility by 7 is a Walk on a Graph. II. […]
22 December 2010, 8:14 pmhahn:
wow cool!
1 January 2011, 12:21 amawesome!
faith:
what method is used in making this graph?
15 February 2012, 12:47 amwhat king of graph is this?
Art DuPre':
This graph I like much more than the first one, because it seems I have a little bit of a chance of generalizing it to 13 , 19 etc. I am showing it to my Finite Math class at The College of New Jwesey this semester. I am also showing them the Stern-Brocot trees, which I am studying now. I’m trying to come up with a geometrical way of adding fractions, similar to Gosper’s way by automata.
I would really like to see more graphs for divisibility for larger numbers.
Tanya, I was a friend of Israel and Tanya Gelfand at Rutgers, and I am a vegan like Gelfand was during the last 10 years of his life. I have been one for 41 years.
Thanks,
27 March 2012, 11:58 amArt
Art DuPre':
My friend, David Reimer, at TCNJ, yesterday solved this for any n and any base! I have drawn up the graphs for 7, 13, 17 for base 10 and given it to five or six colleagues at WM Paterson, and some of them saw how they were drawn already.
Is David Wilson the same David Wilson who was a grad student at Rutgers recently?
Thank you for the stimulating graph!
Art
28 March 2012, 1:08 pmTanya Khovanova:
Art,
No, it’s another David Wilson.
3 April 2012, 11:31 amCraig:
Watch out, Disney’s gonna sue you for copying Mickey Mouse!
30 April 2012, 12:28 pmPaul:
Once you realize how and why it works, it’s actually quite easy to create a similar diagrom for any (positive integer) divisor. Here’s the trick:
For any divisor N, create a circle of n-1 nodes and connect them anti-clockwise by black arrows. Put the numbers 0, 1, 2, …, n-1 in them (also in anti-clockwise order).
Let the value for any node be the number in it. Then for p = 0 to n-1, draw a white arrow from node p to node (((10 mod N)*N) mod N).
I think this should work (as long as we’re working with 10-base numbers), but should you find an error, then please let me know by commenting on this site!
30 April 2012, 2:29 pmJason:
If you want to memorize the graph, the black arrows are just +1 MOD 10 and the white arrows are *3 MOD 7
30 April 2012, 3:05 pmPreetum:
Looking at divisibility graphs like this one for binary numbers yields a finite-state-machine that computes the modulo of numbers in linear time (in the number of digits).
30 April 2012, 6:18 pmFollowing your example, I have made binary divisibility graphs for modulo 4, 10, and 100: https://nakkiran.org/personal/other/divisibility-graphs/
7’ye bölünebilme bir grafik boyunca yürümektir | Bilim.org:
[…] Kaynak: https://blog.tanyakhovanova.com/?p=262 […]
1 May 2012, 9:29 amWillie Weaver:
I have been out of that world for many years. I did enjoy working thru the graph and reading the comments. Although I did not understand a lot of it, I did feel my old brain stretching a little.
1 May 2012, 12:17 pmMert Cayir:
What kind of method is used in making this graph and is there any way to make similar graphs for another numbers even they are very big or not transcendental?
1 May 2012, 1:25 pmUn critère visuel de divisibilité par 7 | Blogdemaths:
[…] que je vais décrire a été posté sans véritable explication par un certain David Wilson sur ce blog. J’avoue ne pas savoir s’il en est l’auteur initial ou si cela est connu depuis […]
2 February 2013, 6:17 am25 best math blogs for college students - OnlineDegrees.org:
[…] This blog is about “mathematics, applications of mathematics to life in general, and my life as a mathematician.” Some notable recent posts include The Weights Puzzle, Math Careers and Choices, and Divisibility by 7 is a Walk on a Graph II. […]
11 March 2013, 2:38 pmFiroze:
Brilliant! Thank you!
14 May 2013, 6:52 amUn critère visuel de divisibilité par 7 | Actumaths:
[…] que je vais décrire a été posté sans véritable explication par un certain David Wilson sur ce blog. J’avoue ne pas savoir s’il en est l’auteur initial ou si cela est connu depuis […]
22 May 2013, 8:30 pmUn critère visuel de divisibilité par 7 | Actumaths:
[…] été posté sans véritable explication par un certain David Wilson sur ce blog. J’avoue ne pas savoir s’il en est l’auteur initial ou si cela est connu depuis […]
18 August 2013, 10:42 am7’ye bölünebilme bir grafik boyunca yürümektir – Burada Biliyorum:
[…] Kaynak: https://blog.tanyakhovanova.com/?p=262 […]
28 December 2019, 12:36 pmbolum fragmanlari:
what method is used in making this graph?
12 April 2020, 12:15 pmwhat king of graph is this?