Tanya Khovanova's Math Blog

This is the promised solution to the puzzle Integers and Sequences that I posted earlier. The puzzle is attached below.

Today I do not want to discuss the underlying math; I just want to discuss the puzzle structure. I’ll assume that you solved all the individual clues and got the following lists of numbers.

• 12 42 18 40 30 24 20
• 2 1 132 42 429 14
• 7 9 1 8 5 3 10 4
• 92 117 70 145 35 1 22 12 5
• 137 1 37 13 107 1013 113
• 30 12 2 42 6
• 70 4030 836 7192

Since the title mentions sequences, it is a good idea to plug the numbers into the Online Encyclopedia of Integer Sequences. Here is what you will get:

• not clear
• Catalan numbers with 5 missing: 1, 1, 2, 5, 14, 42, 132, 429
• not clear
• Pentagonal numbers with 51 missing: 1, 5, 12, 22, 35, 51, 70, 92, 117, 145
• Primeval numbers with 2 missing: 1, 2, 13, 37, 107, 113, 137, 1013
• not clear
• Weird numbers with 5830 missing: 70, 836, 4030, 5830, 7192

Your first “aha moment” happens when you notice that the sequences are in alphabetical order and each has exactly one number missing. The alphabetical order is a good sign that you are on the right track; it can also narrow down the possible names of the sequences that you haven’t yet identified. Alphabetical order means that you have to figure out the correct order for producing the answer.

Did you notice that some groups above are as long as nine integers and some are as short as four? In puzzles, there is nothing random, so the lengths of the groups should mean something. Your second “aha moment” will come when you realize that, together with the missing number, the number of the integers in each group is the same as the number of letters in the name of the sequence. This means you can get a letter by indexing the index of the missing number into the name of the sequence.

So each group of numbers provides a letter. Now we need to identify the remaining sequences and figure out in which order the groups will produce the word that is the answer.

Let’s go back and try to identify the remaining sequences. We already know the number of letters in the name of each sequence, as well as the range within the alphabet. The third sequence might represent a challenge as its numbers are small and there might be many sequences that fit the pattern, but let’s try. The results are below with the capitalized letter being the one that is needed for the answer.

• abundAnt
• caTalan
• dEficient or iMperfect
• pentaGonal
• pRimeval
• proNic or proMic
• weiRd

What is going on? There are two sequences that fit the pattern of the third group and the sequence for the sixth group has many names, two of which fit the profile but produce different letters. Now we get to your third “aha moment”: you have already seen some of the sequence names before, because they are in the puzzle. This will allow you to disambiguate the names.

Now that we have all the letters, we need the order. Sequences are mentioned inside the puzzle. You were forced to notice that because you needed the names for disambiguation. Maybe there is something else there. On closer examination, all but one of the sequence names are mentioned. Moreover, with one exception the clues for one sequence mention exactly one other sequence. Once you connect the dots, you’ll have your last “aha moment:” the way the sequences are mentioned can provide the order. The first letter G will be from the pentagonal sequence, which was not mentioned. The clues for the pentagonal sequence mention the primeval sequence, which will give the second letter R, and so on.

The answer is GRANTER.

Many old-timers criticized the 2013 MIT Mystery Hunt. They are convinced that a puzzle shouldn’t have more than one “aha moment.” I like my “aha moments.”

*****

• (the largest integer n such that there exists a Platonic solid with n vertices, a Platonic solid with n edges, and a Platonic solid with n faces)
• (the largest two-digit tetrahedral number)/(the smallest value the second smallest angle of a convex hexagon with all integer degrees can have)
• (the number of positive integers less than 2013 that are divisible by 100, but not divisible by 70)
• (the number of two-digit numbers that produce a square when summed up with their reverse) ⋅ (the smallest number of weighings on a balance scale that guarantees to find the only fake coin out of 100 identical coins, where the fake coin is lighter than other coins)
• (the only two digit number n such that 2ⁿ ends with n) − (the second smallest, and conjectured to be the largest, triangular number such that its square is also triangular)
• (the smallest non-trivial compositorial number that is also a factorial)
• (the sum of the smallest three positive pronic numbers)

*****

• (the digit you get when you sum up the digits of 2013²⁰¹³ repeatedly until you get a single digit) − (the greatest common factor of the indices of the Fibonacci numbers divisible by 13)
• (the largest common divisor of numbers of the form p² − 1 for primes p greater than three) − (the largest sum of digits that can appear on a 12-hour digital clock starting from 1:00 up to 12:59)
• (the largest Fibonacci number, such that it and all positive Fibonacci numbers less than it are deficient) + (the difference between the sum of all even numbers up to 100 and the sum of all odd numbers up to 100) − (the first digit of a four-digit square that has the first two digits the same and the last two digits the same)
• (the smallest composite Jacobsthal number) ⋅ (the only digit needed to express the number of diagonals of a convex hendecagon)/(the smallest prime divisor of 13²⁰¹³ + 1)
• (the smallest integer the fate of whose aliquot sequence is unknown) + (the largest amount of money in cents you can have in American coins without having change for 2 dollars) − (the repeated number in the aliquot cycle of 95) ⋅ (the second-smallest integer n such that the Russian word for n has n letters)
• (the smallest positive even integer that’s not a totient)

*****

• (the number of letters in the last name of a famous Russian writer whose year of birth many Russians use to help them memorize the digits of e)
• (the number of pluses you need to insert in a row of 20 fives so that the sum is 1000)
• (the number of positive integers less than 2013 such that not all their digits are distinct) − (the number of four-digit numbers with only odd digits) − (the largest Fibonacci square)
• (the number of positive integers n for which the sum of the n smallest positive integers evenly divides 18n)
• (the number of trailing zeroes of 2013!) − (the number of sets in the game of Set such that every feature is different on all three cards) − (an average speed in miles per hour of a person who drives somewhere with a speed of 420 miles per hour, then drives back using the same route with a speed of 210 miles per hour)
• (the smallest fortunate triangular number)
• (the smallest weird number)/(the only prime one less than a cube)
• (the third most probable product of the numbers showing when two standard six-sided dice are rolled)

*****

• (the largest integer number of dollars you can’t pay if you have an unlimited supply of 9-dollar bills and 13-dollar bills) − (the positive difference between the two prime numbers that do not share a unit digit with any other prime number)
• (the largest three-digit primeval number) − (the largest number of distinct SET cards without a set)
• (the number conjectured to be the second-largest number such that two to its power has no zeroes) − (the largest number whose cube has at most two distinct digits and no zeroes)
• (the number of 5-digit palindromic integers in base 5) + (the only positive integer that is five times the sum of its digits)
• (the only Fibonacci number that is a double of a prime) + (the only prime p such that p! has p digits) − (the only fixed point of look-and-say operation)
• (the only number whose concatenation with itself is prime)
• (the only positive integer that that differs by 1 from a square and a nonsquare cube) − (the largest number such that its divisors are each 1 less than a prime)
• (the smallest admirable number)
• (the smallest evil untouchable number)

*****

• (the alphanumeric value of MANIC SAGES) + (the sum of all three-digit numbers you can get by permuting digits 1, 2, and 3) + (the number of two-digit integers divisible by 9) − (the number of rectangles whose sides are composed of edges of squares of a chess board)
• (the integer whose standard Roman numeral representation is alphabetically later than all others) − (the number you get if you divide a three digit number with identical digits by the sum of the digits)
• (the largest even integer that is not a sum of two abundant numbers) − (the digit in the first position where e and π have the same digit)
• (the number formed by the last two digits of the sum: 1! + 2! + 3! + 4! + . . . + 2013!)
• (the only positive integer such that if you sum the digits and the squares of the digits, you get the original number back) + (the largest prime factor of the smallest Carmichael number)
• (the smallest multi-digit hyperperfect number such that more than half of its digits are the same) − (the sum of digits that cannot be the last digits of squares) ⋅ (the largest base n in which 8n is not written like 80) ⋅ (the smallest positive integer that leaves a remainder of 2 when divided by 3, 4, and 5)
• (the smallest three-digit brilliant number) − (the first decimal digit of the number that in hexadecimal gives the house number of Sherlock Holmes)

*****

• (the number of evil minutes in an hour)
• (the number of fingers on ten hands) − (the smallest number such that its square has a digit repeated three times)
• (the number of ways you can rearrange letters of MANIC)/(the number of ways you can rearrange letters of SAGES)
• (the only multi-digit Catalan number with digits in strictly decreasing order)
• (the smallest perfect number)

*****

• (the largest product of positive integers that sum up to 10) + (the smallest perimeter of a rectangle with integral sides of area 120) − (the day of the month of the second Thursday in a January that has exactly 4 Mondays and 4 Fridays)
• (the second-largest number with all distinct digits, such that all the words in its American English representation start with the same letter) + (the largest square-free composite number that contains each of the digits 1, 2, 3, 4 exactly once in its prime factorization) + (the number of ways you can flip a coin 10 times so that the number of heads is the same as the number of tails) + (the smallest positive integer such that 2 to its power contains 2013 as a substring) + (the sum of five prime numbers formed from the digits 2, 3, 5, 7, 8, 9 where each digit is used exactly once) + (the number of days in a year where the day of the month is odious) + (the sum of the digits each of which spelled out has an alphanumeric value equal to the meaning of life, the universe, and everything) ⋅ (the sum of all prime numbers p such that p + 20 and p + 40 are also prime) + (the first digit of the total number of legal moves of the Black king in chess)
• (the second-largest three-letter palindrome in Roman numerals)/((the smallest composite number not divisible by any of its digits)/(the last digit of 2013²⁰¹³) − (the digit in position 2013 of the string formed by concatenation of all integers into one stream: 123456789101112…)) − (the number of days in a year such that the month and the day of the month are simultaneously composite)
• (the second-smallest cube with only prime digits) ⋅ (the smallest perimeter of a Pythagorean triangle)/(the last digit to appear in the units place of a Fibonacci number) + (the greatest common divisor of the sums in degrees of the interior angles of convex polygons with an even number of sides) + (the number of subsets that you can form from the set {1,2,3,4,5,6,7,8,9} that do not contain two consecutive numbers) − (the only common digit of 2013 base 8 and base 9)

Tanya Khovanova and Joel Brewster Lewis

In skyscraper puzzles you have to put an integer from 1 to n in each cell of a square grid. Integers represent heights of buildings. Every row and column needs to be filled with buildings of different heights and the numbers outside the grid indicate how many buildings you can see from this direction. For example, in the sequence 213645 you can see 3 buildings from the left (2,3,6) and 2 from the right (5,6).

In mathematical terminology we are asked to build a Latin square such that each row is a permutation of length n with a given number of left-to-right and right-to-left-maxima. The following 7 by 7 puzzle is from the Eighth World Puzzle Championship.

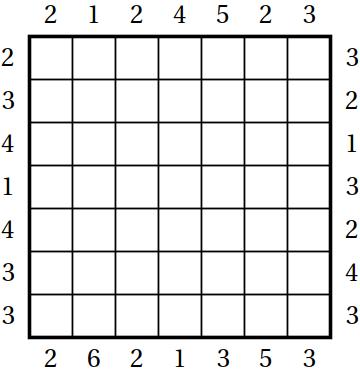
Latin squares are notoriously complicated and difficult to understand, so instead of asking about the entire puzzle we discuss the mathematics of a single row. What can you say about a row if you ignore all other info? First of all, let us tell you that the numbers outside have to be between 1 and n. The sum of the left and the right numbers needs to be between 3 and n+1. We leave the proof as an exercise.

Let’s continue with the simplest case. Suppose the two numbers are n and 1. In this case, the row is completely defined. There is only one possibility: the buildings should be arranged in the increasing order from the side where we see all of them.

Now we come to the question we are interested in. Given the two outside numbers, how many permutations of the buildings are possible? Suppose the grid size is n and the outside numbers are a and b. Let’s denote the total number of permutations by f_n(a, b). We will assume that a is on the left and b is on the right.

In a previous example, we showed that f_n(n, 1) = 1. And of course we have f_n(a, b) = f_n(b, a).

Let’s discuss a couple of other examples.

First we want to discuss the case when the sum of the border numbers is the smallest — 3. In this case, f_n(1, 2) is (n−2)!. Indeed, we need to put the tallest building on the left and the second tallest on the right. After that we can permute the leftover buildings anyway we want.

Secondly we want to discuss the case when the sum of the border numbers is the largest — n+1. In this case f_n(a,n+1-a) is (n-1) choose (a-1). Indeed, the position of the tallest building is uniquely defined — it has to take the a-th spot from the left. After that we can pick a set of a-1 buildings that go to the left from the tallest building and the position is uniquely defined by this set.

Before going further let us see what happens if only one of the maxima is given. Let us denote by g_n(a) the number of permutations of n buildings so that you can see a buildings from the left. If we put the shortest building on the left then the leftover buildings need to be arrange so that you can see a-1 of them. If the shortest building is not on the left, then it can be in any of the n-1 places and we still need to rearrange the leftover buildings so that we can see a of them. We just proved that the function g_n(a) satisfies the recurrence:

Actually g_n(a) is a well-known function. The numbers g_n(a) are called unsigned Stirling numbers of the first kind (see https://oeis.org/A132393); not only do they count permutations with a given number of left-to-right (or right-to-left) maxima, but they also count permutations with a given number of cycles, and they appear as the coefficients in the product (x + 1)(x + 2)(x + 3)…(x + n), among other places. (Another pair of exercises.)

We are now equipped to calculate f_n(1, b). The tallest building must be on the left, and the rest could be arranged so that, in addition to the tallest building, b-1 more buildings are seen from the right. That is f_n(1, b) = g_n-1(b-1).

Here is the table of non-zero values of f_n(1, b).

Now we have everything we need to consider the general case. In any permutation of length n, the left-to-right maxima consist of n and all left-to-right maxima that lie to its left; similarly, the right-to-left maxima consist of n and all the right-to-left maxima to its right. We can take any permutation counted by f_n(a, b) and split it into two parts: if the value n is in position k + 1 for some 0 ≤ k ≤ n-1, the first k values form a permutation with a – 1 left-to-right maxima and the last n – k – 1 values form a permutation with b – 1 right-to-left maxima, and there are no other restrictions. Thus:

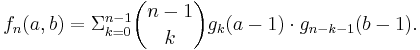
Let’s have a table for f₇(a,b), of which we already calculated the first row:

We see that the first two rows of the puzzle above correspond to the worst case. If we ignore all other constrains there are 675 ways to fill in each of the first two rows. By the way, the sequence of the number of ways to fill in the most difficult row for n from 1 to 10 is: 1, 1, 2, 6, 22, 105, 675, 4872, 40614, 403704. The maximizing pairs (a,b) are (1, 1), (1, 2), (2, 2), (2, 2), (2, 2), (2, 3), (2, 3), (2, 3), (3, 3).

The actual skyscraper puzzles are designed so that they have a unique solution. It is the interplay between rows and columns that allows to reduce the number of overall solutions to one.

Thank you to everyone who helped me to find a host for my Number Gossip website. Some readers and friends even offered me free hosting on their servers. I decided to pay for hosting because I have many specific requirements and that might be a burden on my friends.

On the basis of my readers’ recommendations, I chose Dreamhost as my new webhosting provider. I apologize for the interruption in the flow of the gossip. I know that many people use Number Gossip for birthday gift ideas. I can tell you that on my previous birthday, you could have congratulated me on becoming prime and evil.

The Fibonacci sequence is all about addition, right? Indeed, every element F_n of the Fibonacci sequence is the sum of the two previous elements: F_n = F_n-1 + F_n-2. Looking closer we see that the Fibonacci sequence grows like a geometric progression φⁿ, where φ is the golden ratio. In addition, the Fibonacci sequence is a divisibility sequence. Namely, if m divides n, then F_m divides F_n.

My point: we define the sequence through addition, and then multiplication magically appears by itself. What would happen if we tweak the rule and combine addition and multiplication there?

John Conway did just that: namely, he invented a new sequence, or more precisely a series of sequences depending on the pair of the starting numbers. The sequences are called Conway’s subprime Fibonacci sequences. The rule is: the next term is the sum of the two previous terms, and, if the sum is composite, it is divided by its least prime factor.

Let me illustrate what is going on. First we start with two integers. Let’s take 1 and 1 as in the Fibonacci sequence. Then the next term is 2, and because it is prime and we do not divide by anything. The next two terms are 3 and 5. After that the sum of two terms is 8, which is now composite and it is divided by 2. So the sequence goes: 1, 1, 2, 3, 5, 4, 3, 7, 5, 6, 11 and so on.

The subprime Fibonacci sequences excite me very much. Not only does adding some multiplication to the rule make sense to me, but also, the sequences are fun to play with. I got so excited that I even coauthored a paper about these sequences titled, not surprisingly, Conway’s Subprime Fibonacci Sequences. The paper is written jointly with Richard K. Guy and Julian Salazar, and is available at the arXiv:1207.5099.

We can start a subprime Fibonacci sequence with any two positive numbers. You can see that such a sequence doesn’t grow fast, because we divide the terms too often. We present a heuristic argument in the paper that allows us to conjecture that no subprime Fibonacci sequence grows indefinitely, but they all start cycling. The conjecture is not proven and I dare you to try.

Meanwhile, the sequences are a lot of fun and I suggest a couple of exercises for you:

• Prove that there are no cycles of length two or three.
• Prove that the maximum number in a non-trivial cycle is prime.
• Prove that the smallest number in a non-trivial cycle is more than one. You can prove that it is more than 6 for extra credit.

By the way, a trivial cycle is the boring thing that happens if we start a sequence with two identical numbers n bigger than one: n, n, n, n, ….

Have fun.

I recently published my new favorite math problem:

A deck of 36 playing cards (four suits of nine cards each) lies in front of a psychic with their faces down. The psychic names the suit of the upper card; after that the card is turned over and shown to him. Then the psychic names the suit of the next card, and so on. The psychic’s goal is to guess the suit correctly as many times as possible.
The backs of the cards are asymmetric, so each card can be placed in the deck in two ways, and the psychic can see which way the top card is oriented. The psychic’s assistant knows the order of the cards in the deck; he is not allowed to change the order, but he may orient any card in either of the two ways.
Is it possible for the psychic to make arrangements with his assistant in advance, before the latter learns the order of the cards, so as to ensure that the suits of at least (a) 19 cards, (b) 23 cards will be guessed correctly?
If you devise a guessing strategy for another number of cards greater than 19, explain that too.

If the psychic is only allowed to look at the backs of the cards, then the amount of transmitted information is 2³⁶, which is the same amount of information as suits for 18 cards. This number of guesses is achievable: the backs of every two cards can clue in the suit of the second card in the pair. This way the psychic can guess the suits of all even-numbered cards in the deck. So the problem is to improve on that. Using the info from the cards that the psychic is permitted to turn over can help too.

The problem is from the book Moscow Mathematical Olympiads, 2000-2005. The book and Russian blog discussions provide many different ideas on how to guess more than half of the deck.

Here is the list of ideas.

Idea 1. Counting cards. If you count cards you will know the suits of the last cards.

Idea 2. Trading. As we discussed before, the psychic can correctly guess the suits of even-numbered cards. By randomly guessing the odd-numbered cards she can correctly guess on average the suits of 4.5 additional cards. Unfortunately, this is not guaranteed. But wait. What if we trade the knowledge of the second card’s suit for the majority suit among odd-numbered cards?

Idea 3. Three cards. Suppose we have three cards. Three bits can provide the following knowledge: the majority color, plus the suit of the first and of the second cards in the majority color. Thus, three bits of information will allow the psychic to guess the suits of two cards out of three.

Idea 4. Which card. Suppose the assistant signals the suits of even-numbered cards. With no loss, the psychic can guess the even-numbered card and repeat the same suit for the next card. If this is the plan, the assistant can choose which of the two cards to describe. Which card of the two matches the psychic’s guess provides an additional bit of information.

Idea 5. Surprise. Suppose we have a strategy to inform the psychic about some cards. Suppose the assistant deliberately fails on one of the cards. Then the index of this card provides info to the psychic.

I leave it to my readers to use these ideas to find the solution for 19, 23, 24 and maybe even for 26 cards.

by Andrew Buchanan, Tanya Khovanova, and Alex Ryba

We got this problem from Rados Radoicic:

A 7 by 7 board is covered with 38 dominoes such that each covers exactly 2 squares of the board. Prove that it is possible to remove one domino so that the remaining 37 still cover the board.

Let us call a domino covering of an n by n board saturated if the removal of any domino leaves an uncovered square. Let d(n) be the number of dominoes in the largest saturated covering of an n by n board. Rados’ problem asks us to prove that d(7) < 38.

Let’s begin with smaller boards. First we prove that d(2) = 2. Suppose that 3 dominoes are placed on a 2 × 2 board. Let us rotate the board so that at least two of the dominoes are horizontal. If they coincide, then we can remove one of them. If not, they completely cover the board and we can remove the third one. Similarly, you can check all the cases and show that d(3) = 6.

Now consider a saturated domino covering of an n × n board. We can view the dominoes as vertices of a graph, joining two if they share a cell of the board. No domino can share both cells with other dominoes, or we could remove it. Hence, each domino contains at most one shared cell. This means that all the dominoes in a connected component of the graph must overlap on a single shared cell. Hence, the only possible connected components must have the following shapes:

The largest shape in the picture is the X-pentomino. We can describe the other shapes as fragments of an X-pentomino, where the center and at least one more cell is intact. We call these shapes fragments.

A saturated covering by D dominoes corresponds to a decomposition of the n × n board into F fragments. Note that a fragment with k cells is made from k − 1 dominoes. Summing over the dominoes gives: D = n² − F. Thus, in order to make D as large as possible, we should make F as small as possible. Let f(n) be the minimal number of fragments that are required to cover an n by n board without overlap. Then d(n) = n² − f(n).

Consider the line graph of the n by n board. The vertices of the line graph correspond to cells in the original board and the edges connect vertices corresponding to neighboring cells. Notice that in the line graph our fragments become all star graphs formed by spokes coming out from a single central node. Thus a decomposition of a rectangular board into fragments corresponds to a covering of its line graph by star graphs. Consider an independent set in the line graph. The smallest independent set has the same number of elements as the smallest number of stars that can cover the graph. This number is called a domination number.

Now let’s present a theorem connecting domino coverings with X-pentomino coverings.

Theorem. f(n) equals the smallest number of X-pentominoes that can cover an n by n board allowing overlaps and tiles that poke outside, which is the same as the domination number of the corresponding line graph.

The proof of this theorem and the solution to the original puzzle is available in our paper: “Saturated Domino Coverings.” The paper also contains other theorems and discussions of other boards, not to mention a lot of pictures.

The practical applications of star graph coverings are well-known and widely discussed. We predict a similar future for saturated domino coverings and its practical applications, two examples of which follow:

First, imagine a party host arranging a plate of cookies. The cookies must cover the whole plate, but to prevent the kids sneaking a bite before the party, the cookies need to be placed so that removal of just one cookie is bound to expose a chink of plate. This means the cookies must form a saturated covering of the plate. Of course the generous host will want to use a maximal saturated covering.

For the second application, beam yourself to an art museum to consider the guards. Each guard sits on a chair in a doorway, from where it is possible to watch a pair of adjacent rooms. All rooms have to be observed. It would be a mistake to have a redundant guard, that is, one who can be removed without compromising any room. Such a guard might feel demotivated and then who knows what might happen. This means that a placement of guards must be a saturated domino covering of the museum. To keep the guards’ Union happy, we need to use a maximal saturated covering.

We would welcome your own ideas for applications of saturated coverings.

Is there a way to put a sequence of numbers to music? The system that comes immediately to mind is to match a number to a particular pitch. The difference between any two neighboring integers is the same, so it is logical to assume that the same tone interval should correspond to the same difference in integers. After we decide which tone interval corresponds to the difference of 1, we need to find our starting point. That is, we need to choose the pitch that corresponds to the number 1. After that, all numbers can be automatically matched to pitches.

After we know the pitches for our numbers, to make it into music we need to decide on the time interval between the notes. The music should be uniquely defined by the sequence, hence the only logical way would be to have a fixed time interval between two consecutive notes.

We see that there are several parameters here: the starting point, the pitch difference corresponding to 1, and the time interval between notes. The Online Encyclopedia of Integer Sequences offers the conversion to music for any sequence. It gives you freedom to set the parameters yourself. The sequences do not sound melodic because mathematical sequences will not necessarily follow rules that comply with a nice melody. Moreover, there are no interesting rhythms because the time interval between the notes is always the same.

One day I received an email from a stranger named Michael Blake. He sent me a link to his video on YouTube called “What Pi Sounds Like.” He converted the digits of Pi to music. My stomach hurt while I was listening to his music. My stomach hurts now while I am writing this. He just numbered white keys on the piano from 1 to 9 starting from C. Then he played the digits of Pi. Clearly, Michael is not a mathematician, as he does not seem to know what to do with 0. Luckily for him the first 32 digits of Pi do not contain zero, so Michael played the first several digits over and over. My stomach hurts because he lost the basic math property of digits: the difference between the neighboring digits is the same. In his interpretation the digits that differ by one can have a tone interval of minor or major second in a random order corresponding to his random starting point.

I am not writing this to trash Michael. He is a free man in a free country and can do whatever he wants with the digits of Pi. Oops, I am sorry, he can’t do whatever he wants. Michael’s video was removed from YouTube due to an odd copyright infringement claim by Lars Erickson, who wrote a symphony using the digits of Pi.

Luckily for my readers Michael’s video appears in some other places, for example at the New Scientist channel. As Michael didn’t follow the symmetry of numbers and instead replaced the math rules with some music rules, his interpretation of Pi is one of the most melodic I’ve heard. The more randomly and non-mathematically you interpret digits, the more freedom you have to make a nice piece of music. I will say, however, that Michael’s video is nicely done, and I am glad that musicians are promoting Pi.

Other musicians do other strange things. For example, Steven Rochen composed a violin solo based on the digits of Pi. Unlike Michael, he used the same tone interval for progressing from one number to the next, like a mathematician would do. He started with A representing 1 and each subsequent number corresponded to an increase of half a tone. That is, A# is 2 and so on. Like Michael Blake he didn’t know what to do with 0 and used it for rest. In addition, when he encountered 10, 11, and 12 as part of the decimal expansion he didn’t use them as two digits, but combined them, and used them for F#, G, G# respectively. To him this was the way to cover all possible notes within one octave, but for me, it unfortunately caused another twinge in my stomach.

by David Wilson

We know that tripling the triangular number 1 yields the triangular number 3. The figure shows how we can use this fact to conclude that tripling the triangular number 15 yields the triangular number 45.

Using this new fact, can you modify the figure to find even larger examples of tripling triangles?

I recently stumbled upon some notes (in Russian) of a public lecture given by Vladimir Arnold in 2006. In this lecture Arnold defines a notion of complexity for finite binary strings.

Consider a set of binary strings of length n. Let us first define the Ducci map acting on this set. The result of this operator acting on a string a₁a₂…a_n is a string of length n such that its i-th character is |a_i − a_(i+1)| for i < n, and the n-th character is |a_n − a₁|. We can view this as a difference operator in the field F₂, and we consider strings wrapped around. Or we can say that strings are periodic and infinite in both directions.

Let’s consider as an example the action of the Ducci map on strings of length 6. Since the Ducci map respects cyclic permutation as well as reflection, I will only check strings up to cyclic permutation and reflection. If I denote the Ducci map as D, then the Ducci operator is determined by its action on the following 13 strings, which represent all 64 strings up to cyclic permutation and reflection: D(000000) = 000000, D(000001) = 000011, D(000011) = 000101, D(000101) = 001111, D(000111) = 001001, D(001001) = 011011, D(001011) = 011101, D(001111) = 010001, D(010101) = 111111, D(010111) = 111101, D(011011) = 101101, D(011111) = 100001, D(111111) = 000000.

Now suppose we take a string and apply the Ducci map several times. Because of the pigeonhole principle, this procedure is eventually periodic. On strings of length 6, there are 4 cycles. One cycle of length 1 consists of the string 000000. One cycle of length 3 consists of the strings 011011, 101101 and 110110. Finally, there are two cycles of length 6: the first one is 000101, 001111, 010001, 110011, 010100, 111100, and the second one is shifted by one character.

We can represent the strings as vertices and the Ducci map as a collection of directed edges between vertices. All 64 vertices corresponding to strings of length 6 generate a graph with 4 connected components, each of which contains a unique cycle.

The Ducci map is similar to a differential operator. Hence, sequences that end up at the point 000000 are similar to polynomials. Arnold decided that polynomials should have lower complexity than other functions. I do not completely agree with that decision; I don’t have a good explanation for it. In any case, he proposes the following notion of complexity for such strings.

Strings that end up at cycles of longer length should be considered more complex than strings that end up at cycles with shorter length. Within the connected component, the strings that are further away from the cycle should have greater complexity. Thus the string 000000 has the lowest complexity, followed by the string 111111, as D(111111) = 000000. Next in increasing complexity are the strings 010101 and 101010. At this point the strings that represent polynomials are exhausted and the next more complex strings would be the three strings that form a cycle of length three: 011011, 101101 and 110110. If we assign 000000 a complexity of 1, then we can assign a number representing complexity to any other string. For example, the string 111111 would have complexity 2, and strings 010101 and 101010 would have complexity 3.

I am not completely satisfied with Arnold’s notion of complexity. First, as I mentioned before, I think that some high-degree polynomials are so much uglier than other functions that there is no reason to consider them having lower complexity. Second, I want to give a definition of complexity for periodic strings. There is a slight difference between periodic strings and finite strings that are wrapped around. Indeed, the string 110 of length 3 and the string 110110 of length 6 correspond to the same periodic string, but as finite strings it might make sense to think of string 110110 as more complex than string 110. As I want to define complexity for periodic strings, I want the complexity of the periodic strings corresponding to 110 and 110110 to be the same. So this is my definition of complexity for periodic strings: let’s call the complexity of the string the number of edges we need to traverse in the Ducci graph until we get to a string we saw before. For example, let us start with string 011010. Arrows represent the Ducci map: 011010 → 101110 → 110011 → 010100 → 111100 → 000101 → 001111 → 010001 → 110011. We saw 110011 before, so the number of edges, and thus the complexity, is 8.

The table below describes the complexity of the binary strings of length 6. The first column shows one string in a class up to a rotation or reflections. The second column shows the number of strings in a class. The next column provides the Ducci map of the given string, followed by the length of the cycle. The last two columns show Arnold’s complexity and my complexity.

As you can see, for examples of length six my complexity doesn’t differ much from Arnold’s complexity, but for longer strings the difference will be more significant. Also, I am pleased to see that the sequence 011010, the one that I called The Random Sequence in one of my previous essays, has the highest complexity.

I know that my definition of complexity is only for periodic sequences. For example, the binary expansion of pi will have a very high complexity, though it can be represented by one Greek letter. But for periodic strings it always gives a number that can be used as a measure of complexity.

I wonder what the largest number is that can be represented with one character. Probably 9. How about two characters? Is it 9⁹? What about three or four?

I guess I should define a character. Let’s have two separate cases. In
the first one you can only use keyboard characters. In the second one
you can use any Unicode characters.

I’m awaiting your answers to this.