Tripling a Triangle
by David Wilson
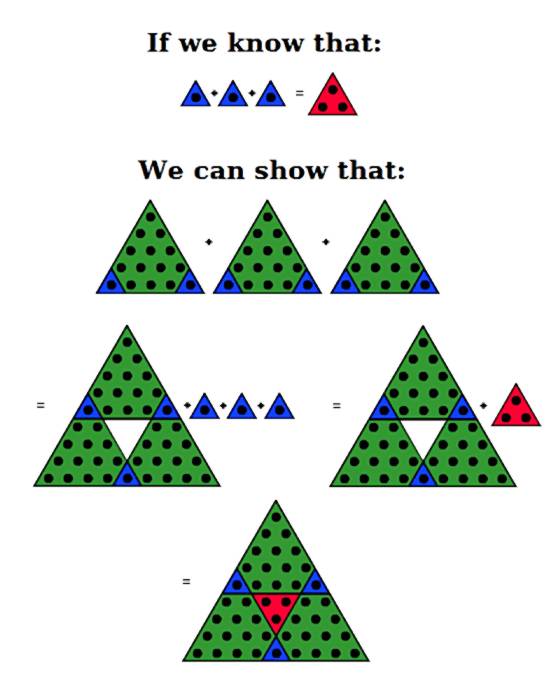
We know that tripling the triangular number 1 yields the triangular number 3. The figure shows how we can use this fact to conclude that tripling the triangular number 15 yields the triangular number 45.
Using this new fact, can you modify the figure to find even larger examples of tripling triangles?
Felix:
Let T_k be the k-th triangular number, with T_1 = 1 and T_2 = 3;
25 August 2011, 10:06 amif 3*T_k = T_n, then the construction above can be generalized to show that 3*T_{2k+(n+1)} = T_{3k+2(n+1)}.
So for every couple (k,n), the next couple can be computed, and there are infinitely many such couples.
The first values of k and n are:
1 2
5 9
20 35
76 132
285 494
1065 1845
3976 6887
…
Nurdin:
I used similar patterns to derive recurrent expressions for triangular numbers: T(2n)=3T(n)+T(n-1), T(2n-1)=3T(n-1)+T(n).
25 August 2011, 4:31 pm