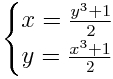33 horsemen are riding in the same direction along a circular road. Their speeds are constant and pairwise distinct. There is a single point on the road where the horsemen can pass one another. Can they ride in this fashion for an arbitrarily long time?
The puzzle appeared at the International Tournament of the Towns and at the Moscow Olympiad. Both competitions were held on the same day, which incidentally fell on Pi Day 2010. Just saying: at the Tournament the puzzle was for senior level competitors; at the Moscow Olympiad it was for 8th graders.
Warning: If you want to solve it yourself first, pause now, because here is the solution I propose.
First, consider two horsemen who meet at that single point. The faster horseman passes the slower one and gallops ahead and the slower one canters along. The next meeting point should be at the same place in the circle. Suppose the slower horseman rides n full circles before the next meeting, then the second horseman could not have passed the first in between, so he has to ride n+1 full circles. That means their speeds should have a ratio of (n+1)/n for an integer n. And vice versa, if their speeds have such a ratio, they will meet at the same location on the circle each time. That means that to solve the problem, we need to find 33 different speeds with such ratios.
As all speed ratios are rational numbers, we can scale speeds so that they are relatively prime integers. The condition that two integers have a ratio (n+1)/n is equivalent to the statement that two integers are divisible by their difference. So the equivalent request to the problem is to find a set of 33 positive integers (or prove non-existence), such that every two integers in the set are divisible by their difference.
Let’s look at examples with a small number of horsemen. For two riders we can use speeds 1 and 2. For three riders, speeds 2, 3 and 4.
Now the induction step. Suppose that we found positive integer speeds for k horsemen. We can add one more horseman with zero speed who quietly stays at the special point and everyone else passes him. The difference condition is satisfied. We just need to tweak the set of speeds so that the lazy horseman starts moving.
We can see that if we add the least common multiple to every integer in a set of integers such that every two numbers in a pair are divisible by their difference, then the condition stays satisfied. So by induction we can find 33 horsemen. Thus, the answer to the problem is: Yes they can.
Now I would like to apply that procedure from the solution to calculate what kind of speeds we get. If we start with one rider with the speed of 1, we add the second rider with speed 0, then we add 1 to both speeds, getting the solution for two riders: 1 and 2. Now that we have a solution for two riders, we add a third rider with speed 0 then add 2 to every speed, getting the solution for three horsemen: 2, 3 and 4. So the procedure gave us the solutions we already knew for two and three horsemen.
If we continue this, we’ll get speeds 12, 14, 15 and 16 for four riders. Similarly, 1680, 1692, 1694, 1695, and 1696 for five riders.
We get two interesting new sequences out of this. The sequence of the fastest rider’s speed for n horsemen is: 1, 2, 4, 16, 1696. And the sequence of the least common multiples for n−1 riders — which is the same as the lowest speed among n riders — is: 1, 1, 2, 12, 1680, 343319185440.
The solution above provides very large numbers. It is possible to find much smaller solutions. For example for four riders the speeds 6, 8, 9 and 12 will do. For five riders: 40, 45, 48, 50 and 60.
I wonder if my readers can help me calculate the minimal sequences of the fastest and slowest speeds. That is, to find examples where the integer speed for the fastest (slowest) horseman is the smallest possible.
Share:





![]()