Archive for the ‘Puzzles’ Category.
30th January 2013, 04:12 pm
When the MIT Mystery Hunt was about to end, I asked my son Sergei, who was competing with the team “Death from Above,” what his favorite puzzle was. I asked the same question to a random guy from team “Palindrome” whom I ran into in the corridor. Surprisingly, out of 150 puzzles they chose the same one as their favorite. They even used similar words to describe it. Calling it a very difficult and awesome puzzle, they both wondered how it was possible to construct such a puzzle.
The puzzle they were referring to is “In the Details” by Derek Kisman, which you can see below.
TWELEVELTWONSHELMUMUOERAIYRANL
QAPIUNPIQAYDPEPIRPRPKVOYESOYOR
ELRATFDTELDTTFDTBWNLMUTFONYDWJ
PIOYJMHAPIHAJMHAAOORRPJMYDANFC
MUOZCGTFBWIRYDHIRAIRTFNCUENCUE
RPVQUHJMAOHKANJUOYHKJMZKBNZKBN
IRONSHOZGOTFUEELTFOEELUEYDOETF
HKYDPEVQDNJMBNPIJMKVPIBNANKVJM
BWIYNLTFSHHIELTWGOYDONDTYDHIOE
AOESORJMPEJUPIQADNANYDHAANJUKV
SHDTYDRPBWUEBWIYTWTWTFYDMUELMU
PEHAANAJAOBNAOESQAQAJMANRPPIRP
ONTWELBWLMSHELTFUEBWBWLMOZEVHI
YDQAPIAOGIPEPIJMBNAOAOGIVQUNJU
DTCGUEYDRPEVNCIREVIRTWUEUETWON
HAUHBNANAJUNZKHKUNHKQABNBNQAYD
IRUERAMUTFELTWONTFOEOEEYDTNLYD
HKBNOYRPJMPIQAYDJMKVKVHWHAORAN
ELGORPNCTFDTYDSHYDELPKTFOZRACG
PIDNAJZKJMHAANPEANPIDFJMVQOYUH
DTMUWJOETFYDELMUMUGORAONIRDTCG
HARPFCKVJMANPIRPRPDNOYYDHKHAUH
| BOUNDARY |
HENON |
LEVY DRAGON |
SCALING |
| BROWNIAN |
HILBERT |
LYAPUNOV |
SPACE |
| CAUCHY |
HURRICANE |
MANDELBROT |
STRANGE |
| CURLICUE |
ITERATE |
NEURON |
TAKAGI |
| DE RHAM |
JULIA |
NURNIE |
TECTONICS |
| DIMENSION |
LEIBNIZ |
POWER LAW |
T-SQUARE |
| ESCAPE |
LEVEL ONE |
RAUZY |
WIENER |
| HAUSDORFF |
LEVEL TWO |
RIVER |
YO DAWG |
_ _ _ _ _ _ _ _
The puzzle looks like a word search, but I can tell you up-front: you can’t find all the words in the grid. You can only find six words there. So there is something else to this puzzle. I will discuss the solution later. Meanwhile I will ask you very pointed questions:
- Where are the other words?
- What is the meaning of LEVEL TWO staring at us from the first row?
- Where is LEVEL ONE?
- What do these very non-random words have in common?
Share:





29th January 2013, 09:06 pm
The easiest of the puzzles I made for the MIT Mystery Hunt 2013 was “Something in Common.” I collaborated on this puzzle with Daniel Gulotta. Ironically, it was the most time-consuming of my puzzles to design — well over a hundred hours. I can’t tell you why it took me so long without revealing hints about the solution, so I will wait until someone solves it.
I received a lot of critique from my editors for suggesting puzzles that were too easy. When, during the test-solve, I realized that this puzzle was one of the easiest in the hunt, I requested permission to make it harder. It would not actually have been difficult to make it harder: I could have just replaced some specific words with more general ones. Unfortunately, we didn’t have time for a new test-solve, so the puzzle stayed as it was. That turned out to be lucky.
This puzzle was in the last round. By the time the last round opened, we knew that the hunt was much more difficult than we had anticipated. I was afraid that people were getting angry with difficult puzzles and so I was very happy that I hadn’t changed this puzzle. By the time the teams started submitting answers to it, people were exhausted. Manic Sages increased the speed with which options to buy answers to puzzles were released. I was ecstatic that this puzzle was one of the few puzzles in the last round that was solved, not bought with options. Here is the puzzle:
- While everyone was discussing which color to paint the room, the counselor was dreaming about a real chocolate sundae. A walk-in walked into the reception in honor of a regular phenomenon visible every four hours or so. The client just wanted to find his dog in order to provide a permanent shortcut to another part of space; instead, he found something else.The Federation didn’t want to buy a lemon, so their lawyer used a spider to type the password. They discovered that the creatures glow in the dark and the perceptive negotiator won the bid. While they were waiting for the results of the shuttle trip, they turned the lights off to hunt them. The bird-like sounds were coming from under the floor. They used alcohol to save the woman’s life, which was a big mistake. She refused to be his conscience, instead she used her new untapped power of light to save the world; she already had a job as a counselor.
- Their daughter disappeared two months ago, whereas they needed to keep the wounded survivor steady. The African activist was kidnapped by rebels when she was a teenager. While some people were building a boat on the beach, she escaped from her kidnappers. He said that the reward had been withdrawn to eliminate the financial incentive to lie. They needed to perform a blood transfusion, but they didn’t have the proper instruments. By his false statement, he removed over-claimers: people lying to get attention. He needed to write vows. They read surprise at the unexpected labor in the woods in the boy’s face. It was clear that the boy had never looked into the backpack.She described horrors she had seen: rape, torture, massacres carried out by child soldiers, the doctor losing his own blood to help the wounded survivor. There was no deception leakage, but she seemed anxious, so the doctor couldn’t go and deliver the baby. They needed to find the other girl before noon, and the crushed leg made blood transfusion impractical. His vows were self-referential. He talked about how he couldn’t write the vows. While the doctor played 20 questions one man died and another was born. The girl wasn’t answering, but the doctor read her micro-expressions. The writer touched her ear and exposed her lies. At the end the doctor suspected murder, and the book was withdrawn.
- She took pictures in an abandoned house and jumped off the roof. Two girls came back to investigate. He was surprised by a basket of cookies and a statue that was in the wrong place. A new drug hit the streets making people see things, like old pictures of a woman who looked exactly like her friend. He started seeing his dead father: when people die in the past, they produce energy in the present.They were the two most powerful people on the planet. For wedding preparations she got a list of 17 DVDs. His partner started hallucinating about her ex. People do not understand time. Naomi’s ability caused all this mess: the box left them behind. The only place where she didn’t use gloves was her garden. The dinner guests tried her chicken, and, as a consequence, they were stuck looking at each other forever. The drugged cookies were a gift to help resolve their issues. Because of that, she gave him the shorthand transcripts to complete the cycle.
- Did she fall asleep while they were discussing the dead boy’s name? The price tag was exorbitant for a witness to identify the defendant. The woman would be everything he wanted and needed. She was a security guard chewing gum. The witness changed her testimony: they went to the woods and were water-rafting, rock-climbing, and arrow-shooting. As she was not the first girl he brought to the woods, the jury gave a verdict of “Not Guilty.”The detective was in court, though it wasn’t his case. She needed to stop talking and start running. Shit always rolls downhill. Poisoned water made her see things she was not supposed to remember like a shitty orange couch outside. In spite of the background check the client was a psychopath who was moved from uptown to the fucking low-rises. Shoulder to the wheel. Dead witness, mother-fucker.
- A little girl was humming about the dark side. The Wicca group was boring, and the new invention was making whooshing sounds. While a laryngitis epidemic took over the town, the noise-eater got turned on by accident.The princess’s scream would kill the monsters, while the monster machine killed its own remote control. She and her future boyfriend discovered each other’s secrets. The dark side is waiting.
- The experiment in the gay club was very important to him. He was a semi-cute boy-next-door type and his shuttle trip was supposed to be easy. There is more to a guy than cock size, and he was being pulled. He was injected with something and started to understand everyone. They were a bald priestess and a warrior with a very nice butt. They offered you a discount if you bought the butt and the bulge together.They were approaching a commerce planet in Pennsylvania. They escaped and were standing on the roof of a hospital. She was sending a transmission, while the older man was running his tongue along the young man’s spine. The girl tried to protect him, believing his story, but was arrested for contamination. Fuck. He had a baby, two babies. He distracted the guards with a puzzle ring. And while they were painting his black car with a pink derogatory word, they escaped.
- He was drinking before operating on his fiancée. What kind of a father kills people? Tonight was the night he would finally sleep, and drinking was the only way for him to stop his hands from shaking. The limo driver kidnapped him while she watched herself die in the mirror. While being sleep-deprived he conducted a test. Nothing was wrong, except he brought the wrong documents to court. The criminal walked, but, unexpectedly, he couldn’t feel his leg and couldn’t walk anymore. There was a lot of blood and the body was not filtering iodine. He took a picture of the actor falling into a coma with his blood-spatter camera.His girlfriend wanted to buy a firm mattress to have sex. He preferred to sleep on a water-bed and told the secret of his bloody hobby to his baby. It was not an infection, it was an allergy, so he changed his plan of where to grab the victim. The case was solved because of the bubbles in the glass. He was killing for his son now. The patient was indeed allergic and crashed his car.
- The woman died two weeks ago, but her car accident was yesterday. There was so much blood and, for some reason, ice. Jane Doe wasn’t the girl’s sister. Melting speed and surface tension could help the calculation. They came to pay their respects but the celebration was postponed. They brought personal effects to drop off. If the couple’s daughter was like their mother, then they themselves were like their grandparents. The idea to ask the grandmother resulted in a kiss.Their planet had been on the verge of a golden age, then everything fell apart. She brought some clothes, a toothbrush, shampoo and some other things to the detention center. “Don’t let the history repeat itself,” the worshiper of the second in command said. She didn’t know what the red string was for. The teen’s sister told him stories about another galaxy, and the war and the algorithm that might find the dead man’s favorite coffee place and, consequently, solve the case. The kidney operation was in a hotel. They didn’t expect to see the body, but there it was. She touched the body to reveal emptiness inside. At the end they gathered in his house for dinner as usual. He had to save Courtney’s future body before everything blew up and put the red sticker on his license.
- After retirement, he came back to an unsolved murder case; he remembered a kiss in flashbacks. He drove to the lake where the accidental drowning happened. He lured everyone involved to the lake, and, after having sex, he told her that he wanted a real marriage. They wanted their child to be born on the new planet. The doctor was one of the suspects. The couple was already in the cabin, and he doubted that he was the one who she really wanted.The young man was murdered, and everyone thought that the detective was the real target. The man went to look for sneakers during the boxing match. The nosy lady-writer dropped names to persuade the sheriff to look into the cabin. The admiral challenged the chief to join him in the ring. They didn’t find the sneakers, and they shouted this to the skies. The lady solved the murder, as usual, while the boxing match became too personal and people started leaving.
Share:





26th January 2013, 11:15 am
The second “instructioned” puzzle is Portals by Palmer Mebane. It is an insanely beautiful and difficult logic puzzle that consists of known puzzle types interconnected to each other through portals. Here Palmer Mebane explains how portals work:
“Each of the ten puzzles corresponds to a color, seen above the grid where the name of the puzzle is written. The grid contains nine square areas, one each of the other nine colors. These are portals that connect the puzzle to one of the other nine, as denoted by the portal color. Each puzzle’s rules define which squares of their solution are “black”. On the portal squares, the two puzzles must agree on which squares are black and which are not. For instance, if in the red grid the top left square of the blue portal is black, then in the blue grid the top left square of the red portal must also be black, and vice versa.”
On the Portals puzzle page you can find the rules for how each individual game is played and how to shade areas. The puzzle requires a lot of attention. It took us a long time to test-solve it. If you make a mistake in one grid it will propagate and will lead to a contradiction in another grid, so it is difficult to correct mistakes. If you do make a mistake, you are not alone: we kept making mistakes during our test-solve. Because of the difficulty of tracing back to the source of the error, we just started anew, but this time making sure that every step was confirmed by two people. Working together in this way, we were able to finish it.
If you do not care about the extraction and the answer, ignore the letter grid in the middle and enjoy the logic of it.

Share:





26th January 2013, 11:02 am
There were a couple of puzzles during the MIT Mystery Hunt that were not so mysterious. Unlike in traditional hunt puzzles, these puzzles were accompanied by instructions. As a result you can dive in and just enjoy solving the logic part of the puzzle without bothering about the final phase, called the extraction, where you need to produce the answer.
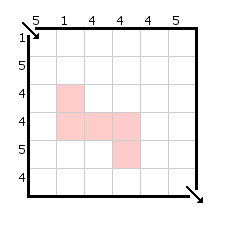
The first puzzle with instructions is Random Walk by Jeremy Sawicki. I greatly enjoyed solving it. In each maze, the goal is to find a path from start to finish, moving horizontally and vertically from one square to the next. The numbers indicate how many squares in each row and column the path passes through. There are nine mazes in the puzzle of increasing difficulty. I am copying here two such mazes: the easiest and the toughest. The colored polyomino shapes are needed for the extraction, so you can ignore them here.
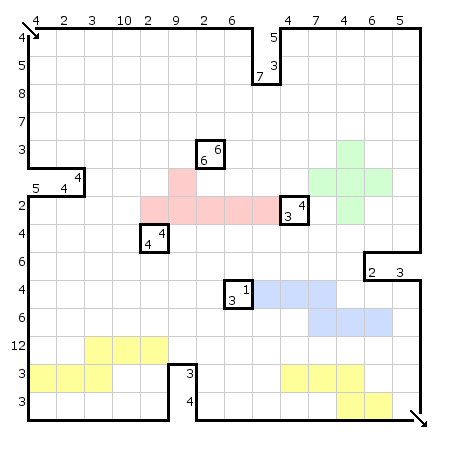
Share:





25th January 2013, 05:10 pm
Today I have a special treat for you. Here is the first of several puzzles that I plan to present from the 150 that we used in the MIT Mystery Hunt 2013. Keep in mind that although the puzzles have authors, they were the result of a collaboration of all the team members. In many instances editors, test-solvers and fact-checkers suggested good ways to improve the puzzles.
I wrote the puzzle Open Secrets jointly with Rob Speer. The puzzle was in the opening round, which means it is not too difficult. By agreement the answers to the puzzles are words or phrases. I invite my readers to try this puzzle. I will post the explanation in about two weeks.

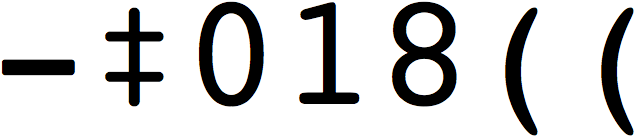
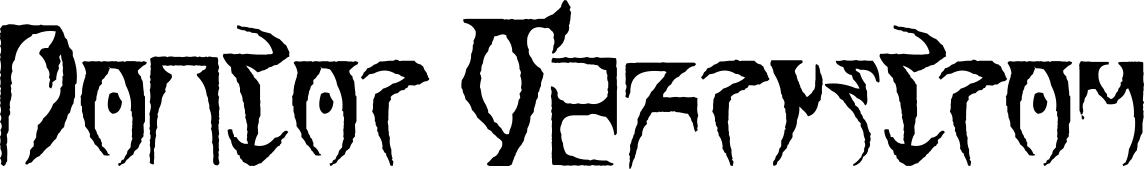



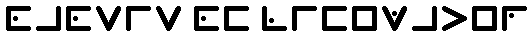


Share:





23rd January 2013, 12:06 pm
10th November 2012, 09:58 am
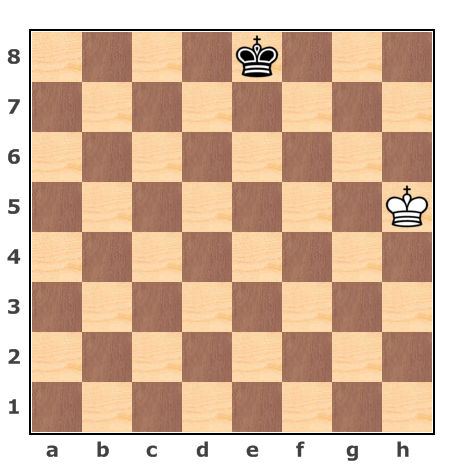
I discovered the following chess puzzle on a Russian blog for puzzle lovers. It is a helpmate-type puzzle. Black cooperates with White in checkmating himself. In this particular puzzle Black starts and helps White to win in one move.
Oops. Something is not quite right. There are not enough pieces on the board. To recover the missing pieces in order to solve the puzzle, you need to retrace your steps. If Black and White go back one move each, they will be able to cooperatively checkmate Black in one move. Find the position one move back and the cooperative checkmate.
Share:





7th November 2012, 04:03 pm
For my every class I try to prepare a challenge problem to stretch the minds of my students. Here is a problem I took from Adam A. Castello’s website:
There is a ceiling a hundred feet above you that extends for- ever, and hanging from it side-by-side are two golden ropes, each a hundred feet long. You have a knife, and would like to steal as much of the golden ropes as you can. You are able to climb ropes, but not survive falls. How much golden rope can you get away with, and how? Assume you have as many hands as you like.
The next problem I heard from my son Sergei:
You are sitting at the equator and you have three planes. You would like to fly around the equator. Each plane is full of gas and each has enough gas to take you half way around. Planes can transfer gas between themselves mid-air. You have friends, so that you can fly more than one plane at once. How do you fly around the equator?
Share:





3rd October 2012, 08:24 pm
29th September 2012, 08:22 pm