I stumbled on this puzzle on Facebook the day of the World Cup finals. How timely!
Puzzle. Sixteen teams play a single-elimination tournament, where the losing team is immediately out. The teams have different rankings, and a higher-ranking team always wins against a lower-ranking team. The initial seeding is random. In the semifinals, A won against B, and C won against D. Given that B is stronger than D, what is the probability that A will become the champion?
Consider a group of people in which some are friends. We assume that friendship is symmetric: if Alice is Bob’s friend, then Bob is Alice’s friend. That means we can build a friendship graph where vertices are people and edges correspond to friendships. Let’s assume that every person has at least one friend, so the friendship graph doesn’t have isolated vertices.
Darla needs to conduct research by surveying random pairs of friends. But first, she has to find those pairs. To ensure that the pairs are randomly selected, she must pick two random people from the group, contact them, and ask them whether or not they are friends. If they are, she gives them her questionnaire. If not, Darla wasted tons of time and had to keep looking.
The group she is surveying is enormous. So, when she picks two random people, they typically have never even heard of each other. Bother!
Darla decides to speed up the process. She would pick a random person, ask them for a list of friends, and then randomly pick one person from the list. Since every person has at least one friend, Darla always ends up with a filled questionnaire.
Puzzle question. Why is Darla’s method wrong? Can you describe the pairs of friends her method favors?
As my readers know, I run a PRIMES STEP program, where we conduct mathematical research with students in grades 6 through 9. Last year, our junior group wrote the paper, The Struggles of Chessland, which is now posted on the arXiv.
This is the funniest paper ever written at PRIMES STEP. In the paper, the King, with his self-centered Queen and their minions, try to protect their lands in the Bermuda triangle, called the Chessland, which consists of square islands of different sizes.
In the first part of their fairy tale, the King, his lazy Queen, and other chess pieces are trying to survey their islands. The first volunteer for this surveying job is the Knight. The Knight starts somewhere on an island and walks around it by using the knight’s moves in chess. The goal is to see every cell, and a Knight can see all cells that are a knight’s move away from where he is standing. In other words, every cell is either visited by the Knight or is one knight’s move away from a visited cell. In mathematical terms, the Knight walks a path that is a domination set on a knight’s graph.
The students found a lot of such paths. The picture shows a surveying path for the Knight for the island of size 7. The students called this pattern a shoelace pattern. They used similar shoelaces to survey any island of size 7 or larger. However, when I look at the picture, I see a cat.
Other chess pieces survey the land too. Funnily, the King surveys better when he is drunk. Do you know why? Take a look at the paper.
After all the islands had been surveyed, enemy spies started to appear in Chessland, and our band of chess pieces tried to trap them. My students invented the rules for trapping enemies. An example of the black Queen being trapped is in the picture below, and the rules are the following. Wherever the black Queen might move, should be under attack by a white queen. Also, white queens can’t directly attack the black Queen, or each other.
Oh! I forgot to mention: the trapping should use as few white queens as possible. Also, if the enemy is not a queen but another kind of chess piece, it can only be trapped by its own kind.
The trapping can be described in terms of graph theory. The black Queen is located at a vertex of the queen’s graph. The white queens should be positioned at vertices in such a way that they are not neighbors of the black Queen or each other. In addition, any vertex that is a neighbor of the black Queen, has to be a neighbor of at least one white queen.
This year’s PRIMES STEP project was a real chess adventure!
The 2018 International Collegiate Programming Contest (ICPC) had a very hard problem which is of interest to mathematicians. The problem was proposed by super-coder Derek Kisman. Here is the problem as it was presented at the contest.
Problem J. Uncrossed Knight’s Tour. A well-known puzzle is to “tour” all the squares of an 8 × 8 chessboard using a knight, which is a piece that can move only by jumping one square in one direction and two squares in an orthogonal direction. The knight must visit every square of the chessboard, without repeats, and then return to its starting square. There are many ways to do this, and the chessboard size is manageable, so it is a reasonable puzzle for a human to solve.
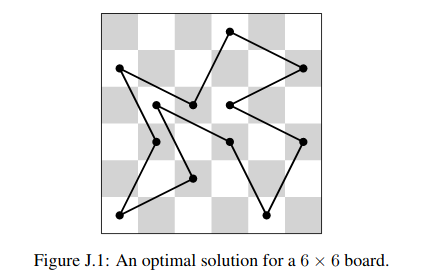
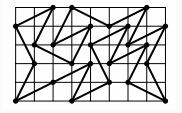
However, you have access to a computer, and some coding skills! So, we will give you a harder version of this problem on a rectangular m × n chessboard with an additional constraint: the knight may never cross its own path. If you imagine its path consisting of straight line segments connecting the centers of squares it jumps between, these segments must form a simple polygon; that is, no two segments intersect or touch, except that consecutive segments touch at their common end point. This constraint makes it impossible to visit every square, so instead you must maximize the number of squares the knight visits. We keep the constraint that the knight must return to its starting square. Figure J.1 shows an optimal solution for the first sample input, a 6 × 6 board.
The input consists of a single line containing two integers m (1 ≤ m ≤ 8) and n (1 ≤ n ≤ 1015), giving the dimensions of the rectangular chessboard.
Mathematicians know many things about knight tours on a standard 8 × 8 chessboard. But one of the limits in this puzzle is so huge, that the answer to this computational puzzle constitutes a new mathematical discovery. Unsurprisingly, no one solved this puzzle during the contest. A well-written solution summary is available on the ICPC website. The solution requires dynamic programming and a realization that tours have to have repeating patterns.
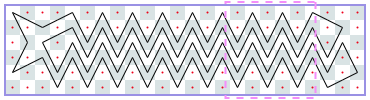
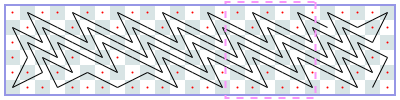
Since no one solved this problem during the competition, it is useful that, in addition to the solution summary, Derek posted his innovative code online. The two figures below (courtesy of Derek Kisman) show his answer for the longest closed tour on a 6 × 24 board and the longest open tour on a 6 × 26 board.
Derek got interested in uncrossed knight’s tours after reading my blog post, 2014 Math Festival in Moscow, where I presented the following problem given at that festival to 7th graders.
Problem. Inside a 5 × 8 rectangle, Bart draws closed paths that follow diagonals of 1 × 2 rectangles. Find the longest possible path.
The 2014 Math Festival organizers offered an extra point for every diagonal on top of 16. It is funny that the organizers obfuscated that it is useless to try and find 17 diagonals, as the number of diagonals has to be even. The official solution, shown below, had 24 diagonals.
In the solution booklet, the organizers mentioned that they did not know the best answer to their own question. They hoped that the longest possible path matched their official solution.
In Derek’s notation, the above problem is equivalent to finding the largest uncrossed knight’s closed tour on a 6 × 9 grid. And Derek proved that, indeed, 24 is the largest tour. While proving this, he also calculated the answer for gazillions of other boards.
We can go further: beyond gazillions. Let’s consider what happens on m × n boards, where m is fixed, and n is astronomically large. Suppose fm(n) is the largest size of an uncrossed knight’s closed tour on the m × n board and gm(n) is the largest size of an uncrossed open tour.
The answer has repeating patterns everywhere except around the ends of the board. We would expect that the number of possible repeating patterns is finite. Moreover, for large boards, only the densest patterns would appear. This means that asymptotically, both functions f and g are linear functions of n. On top of that, as each pattern is periodic, the behavior at the ends of the long boards should become periodic as well. Hence, the difference functions of f and g for fixed m would eventually become periodic. (Here, the f’s difference function, which I denote D(fm) is defined as follows: D(fm)(n) = fm(n+1) – fm(n).)
That means we can solve a more difficult problem. We do not need the limits for n. It should be possible to calculate these functions for a given m and any n (even if n is way more than a gazillion). I am being over-optimistic here. First, we need some mathematical theory to find the bounds for where the periodic behavior has to start and estimate the size of the period. Suppose we can prove that for D(f6)(n), the eventual period has to start before n reaches A, and the length of the eventual period is not more than B. Then, we need to calculate the A + 2B values of the function f6(n) to know the function for any n.
Derek actually calculated the functions fm(n) and gm(n) for m up to 9 and n up to infinity. More precisely, he found the cycles I am describing above. What a mindblowing achievement!
My former IMO coach, Gregory Galperin, converted a famous joke into a logic puzzle, adding a variation.
Puzzle. Ten logicians walked into a cafe. Each knew whether they wanted tea or coffee, but no one knew each other’s preferences. When they sat at a table, the waiter asked loudly, “Will everyone be having coffee?” Then the waiter went around the table, writing down each person’s answer. There were three possible answers: “I don’t know”, “Yes”, and “No”. All answers were truthful and spoken loudly so that all group members heard them.
Suppose the first nine people said, “I don’t know”, and the tenth person said, “Yes”. How many of them wanted coffee?
Suppose the sixth and the seventh answers were not the same. How many people said, “I don’t know”, how many said, “No”, and how many said, “Yes”. Find the smallest number of people who for sure would have ordered coffee and the smallest number who for sure would have wanted tea?
