The Struggles of Chessland
As my readers know, I run a PRIMES STEP program, where we conduct mathematical research with students in grades 6 through 9. Last year, our junior group wrote the paper, The Struggles of Chessland, which is now posted on the arXiv.
This is the funniest paper ever written at PRIMES STEP. In the paper, the King, with his self-centered Queen and their minions, try to protect their lands in the Bermuda triangle, called the Chessland, which consists of square islands of different sizes.
In the first part of their fairy tale, the King, his lazy Queen, and other chess pieces are trying to survey their islands. The first volunteer for this surveying job is the Knight. The Knight starts somewhere on an island and walks around it by using the knight’s moves in chess. The goal is to see every cell, and a Knight can see all cells that are a knight’s move away from where he is standing. In other words, every cell is either visited by the Knight or is one knight’s move away from a visited cell. In mathematical terms, the Knight walks a path that is a domination set on a knight’s graph.
The students found a lot of such paths. The picture shows a surveying path for the Knight for the island of size 7. The students called this pattern a shoelace pattern. They used similar shoelaces to survey any island of size 7 or larger. However, when I look at the picture, I see a cat.
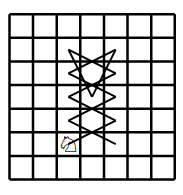
Other chess pieces survey the land too. Funnily, the King surveys better when he is drunk. Do you know why? Take a look at the paper.
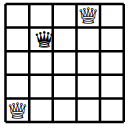
After all the islands had been surveyed, enemy spies started to appear in Chessland, and our band of chess pieces tried to trap them. My students invented the rules for trapping enemies. An example of the black Queen being trapped is in the picture below, and the rules are the following. Wherever the black Queen might move, should be under attack by a white queen. Also, white queens can’t directly attack the black Queen, or each other.
Oh! I forgot to mention: the trapping should use as few white queens as possible. Also, if the enemy is not a queen but another kind of chess piece, it can only be trapped by its own kind.
The trapping can be described in terms of graph theory. The black Queen is located at a vertex of the queen’s graph. The white queens should be positioned at vertices in such a way that they are not neighbors of the black Queen or each other. In addition, any vertex that is a neighbor of the black Queen, has to be a neighbor of at least one white queen.
This year’s PRIMES STEP project was a real chess adventure!
Share:
Leave a comment