Symmetries of k-Symmetric Permutations
I am fascinated by 3-symmetric permutations, that is, permutations that contain all possible patterns of of size three with the same frequency. As I mentioned in my recent post 3-Symmetric Permutations, the smallest non-trivial examples are in size 9.
When I presented these examples at a combinatorics pre-seminar, Sasha Postnikov suggested to draw the permutations as a graph or a matrix. Why didn’t I think of that?
Below are the drawings of the only two 3-symmetric permutations of size 9: 349852167 and 761258943.
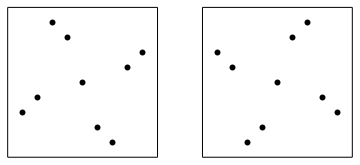
As I already mentioned in the aforementioned essay the set of 3-symmetric permutations is invariant under the reversal and subtraction of each number from the size of the permutation plus 1. In geometrical terms it means reflection along the vertical midline and central symmetry. But as you can see the pictures are invariant under 90 degree rotation. Why?
What I forgot to mention was that the set of k-symmetric permutations doesn’t change after the inversion. In geometrical terms it means the reflection with respect to the main diagonal. If you combine a reflection with respect to a diagonal with a reflection with respect to a vertical line you get a 90 degree rotation. Overall, the symmetries of the k-symmetric permutations are the same as all the symmetries of a square. Which means we can only look at the shapes of the k-symmetric permutations.
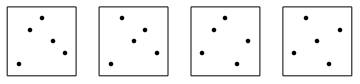
There are six 2-symmetric permutations: 1432, 2341, 2413, 3142, 3214, 4123. As we can see in the picture below they have two different shapes.

Here is the list of all 22 2-symmetric permutations of size 5: 14532, 15342, 15423, 23541, 24351, 24513, 25143, 25314, 31542, 32451, 32514, 34152, 34215, 35124, 41352, 41523, 42153, 42315, 43125, 51243, 51324, 52134. The list was posted by Drake Thomas in the comments to my essay. Up to symmetries the permutations form four groups. Group 1: 14532, 15423, 23541, 32451, 34215, 43125, 51243, 52134. Group 2: 15342, 24351, 42315, 51324. Group 3: 24513, 25143, 31542, 32514, 34152, 35124, 41523, 42153. Group 4: 25314, 41352. The picture shows the first permutation in each group.
Angelo Scordo:
First of all my compliments for your very interisting blog. You have succeeded in transmitting to me also the passion for 3-symmetricic permutations.
I want to add something to the 3-symmetric permutations of size 9. I have calculated the distance of all permutation of size 9 from the 3-symmetric status.
I used the variance to measure it. Of course the two 3-simmetric permutation have variance equal to zero. I searched which are the most distant from them, and
found out that they are [1, 2, 3, 4, 5, 6, 7, 8, 9] and [9, 8, 7, 6, 5, 4, 3, 2, 1] with a variance of 980. All the other permutations have intermediate variance from 0 to 980 and the most numerous group has 2328 elements with variance = 35.67. Both, the distribution of variances and the elements of each group are very
irregular. (the previous comment has a calculation error).
Excuse for my poor english, but my mother language is italian.
Thank you in advance.
27 November 2018, 9:24 amAngelo Scordo:
I investigated a little bit further the symmetric behavior of permutations expecially the 2-symmetric one’s.
14 December 2018, 2:09 pmI found the followings:
If you think the points in your graph as having a unitary mass, the center of gravity have coordinates (n/2, n/2).
More interesting is the behaviour of the moment of inetia J.
If we calculate the J with respect to a axis perpendicular to the plane of mass and passing for the center of gravity, the moment of inertia
vary in the same manner as the variance from the 2-symmetric status that I mentioned in my comments to 3-symmetric permutation.
In a first moment I thought that the two measures where isomorphic. But further investigation indicated that the moment of inertia is able to
identify the differences between the 6 2-symmetric permutations, in fact the two central in your graph 15423, 23541 are a perfect distribution
and give the same value of J for every axis passing for the center of gravity. The other four, even if they give the same value with reference
to the vertical and oriziontal axis have a different value for different axis. In fact the moment of inertia in the plane can be represented
as a vector which describe an ellipse with the minimum eccentricity, while the two central make a circle.
On the other end, the permutations: 1234 and 4321 give J=0 if we take an axis passing for the points that represent them. In this case which is
yhe most distant fron the 2-symmetric status, we have that the minimum moment lye on the plane of mass and the maximum is obtained either on
a axis perpendicular to the one passing though the mass or the axis perpendicular to the mass plane and passing for the center of gravity:
This behaviour needs further investigation by a mechanical engineer.
Angelo Scordo:
First of all there are many typing errors one is inetia instead of inertia (line 4), lye instead of lies (line 13).
16 December 2018, 1:58 pmAngelo Scordo:
Another error yhe instead of the (line 13).
Saying better the concept introduced by my comment of 14 December 2018, the different class in which the permutation group can be divided by
16 December 2018, 2:40 pmthe densities order-isomorphic to the permutations of order 2, can be isomorphic to some properties of the principal moments of inertia applyed
to the permutations.
But the principal moments of inertia and the relevant Poinsot’s Ellipsoid can define better the class subdivision and account for the differences
existing inside the 2-symmetric allowing to identify a subgroup of 2 elemets the “2-supersymmetric permutations” for them the Poinsot’s ellipsoid
is a sphere from the other 4, further investigation show that also for them the ellipsoid is a sphere but its center is not coincident with the center
of gravity. This need furter investigation.
Angelo Scordo:
As an aid for the calculation of the center of gravity and of the principal moment of inertia I described the permutation under investigation
16 December 2018, 2:48 pmas a vector of complex numbers using as the real part the place i of the digit inside the permutation and as immaginary part the digit itself P(i).
In this way it is easy to calculate the different moment and even the ellipsoid.
Angelo Scordo:
In 14 december post the center of gravity must be corrected from (n/2,n/2) to ((n+1)/2,(n+1)/2)
22 December 2018, 1:32 pm