Tanya Khovanova's Math Blog

I have an idea for a start-up medical insurance company for Massachusetts. My insurance will have an infinite deductible. That means you pay your own bills. The cost of insurance can be very low, say $100 a year, as I do not need to do anything other than to send you a letter confirming that you have medical insurance. People who otherwise will be fined up to $900 for being uninsured will run in droves to buy my insurance.

I have an even better idea. For an extra fee, I will negotiate with doctors so that you will pay the same amount as medical insurance companies pay to them, which is often three times less than you would pay on your own.

Who am I kidding? I am not a business person, I can’t build a company. But I am looking to buy the insurance I just described.

I am just wondering:

What is the largest integer consisting of distinct digits such that, in its English pronunciation, all the words start with the same letter?

I continue to wonder:

What is the largest integer consisting of the same digit such that, in its English pronunciation, all the words start with distinct letters?

When you name your child there are many considerations to take into account. For example, you should always check that your kids’ initials don’t embarrass them. For example, if the Goldsteins want to name their son Paz, because it means golden in Biblical Hebrew, the middle name shouldn’t be Isaak, or anything starting with I.

Contemporary culture adds another consideration: how easy would it be to find your child on the Internet? I personally find it extremely convenient to have a rare name, because my fans can find my webpage and blog just by googling me. Parents need to decide whether they want their children to be on the first page of the search engine or hidden very far away when someone googles them.

When I named my son Sergei, I knew that there was another mathematician named Sergei Bernstein. But I didn’t think about the Internet. As a result, I confused the world: is my son more than a hundred years old or did Sergei Natanovich Bernstein compete at Putnam?

I decided to see the film The Oxford Murders because I loved the idea of “Frodo” being a graduate student in logic. By Frodo, I mean the actor Elijah Wood, who is very believable as a math student.

At the core of the movie are sequences of numbers and symbols. When the characters started a discussion about how to continue a sequence, I immediately tensed up. Why? Because when people ask what the next element in the sequence is, I get ready to confront them, by explaining that there are many ways to continue a sequence. For example, the sequence — 1, 2, 4 — could be powers of two, or could be Tribonacci numbers, or any of 10,000 sequences that the Online Encyclopedia of Integer Sequences spills out if you plug in 1, 2, 4. That is, if we do not count the infinity of sequences that are not in the Encyclopedia.

To my surprise and relief, the logic Professor, one of the main characters in the movie, explained that there is no unique way to continue a sequence. From that moment on, I relaxed and fell in love with the movie.

The movie is a detective story with a lot of twists and turns. The crimes are related to symbols. The first two symbols are in the picture below. Can you guess the next symbol?

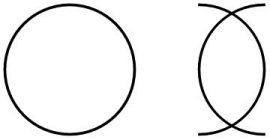
I cannot. There is an irony in the film at this point, because the Professor and the student need to guess the sequence in order to solve the crimes. But the Professor has already explained that there is no unique way to continue. So illogical for a movie about logic.

And what’s worse, the sequence of symbols they finally discover doesn’t make sense. I guess I fell in love with this movie too quickly.

* * *

— I’ve noticed that fools are always sure of themselves, while clever people are doubtful.
— No doubt.

* * *

— What happened to your girlfriend, that really cute math student?
— She’s no longer my girlfriend. I caught her cheating on me.
— I don’t believe that she cheated on you!
— Well, a couple of nights ago I called her, and she told me that she was in bed wrestling with three unknowns.

* * *

A programmer calls the library:
— Can I talk to Kate please?
— She’s in the archive.
— Can you unzip her?

* * *

To protect the population from airplane disasters, Congress has ratified an addendum to the law of gravity.

* * * (invented by David Bernstein)

Energy conservation: it’s not just a good idea; it’s the law.

* * *

— Your computer is such a mess.
— It got a nasty virus.
— And it poured coffee on your keyboard?

* * *

After little Tom learned to count, his father had to start dividing dumplings evenly.

* * *

In spite of the crisis, inflation, and erratic fluctuations of the market, Russian mathematicians promised the president to keep number Pi between 3 and 4 until at least the end of the year.

* * *

A logician rides an elevator. The door opens and someone asks:
— Are you going up or down?
— Yes.

My webpage and my blog generate a lot of emails. I love receiving most of the emails, but if I reply to them, I won’t have time to work on my blog. My favorite type of message is one that is full of compliments, with a note that the writer doesn’t expect a reply.

I am grateful to people who send me things I requested, like pictures of Russian plates, or some interesting number properties. I apologize that it takes me so long to reply.

The emails that I don’t enjoy reading contain amazing elementary proofs of Fermat’s last theorem, or any other theorem on the Millennium list, for that matter. I also do not like when my readers ask me for help with their homework.

Like most people, I’m already dealing with spammers who want to enlarge the body parts I do not have or to slim the ones I do have. However, if you do need to send me millions of dollars that I won in your lottery, there is no reason to waste time on email exchanges: you can process them through my “donate” button.

You are welcome to contact me, but ….

I already gave an example of the kinds of problems that were given to Jewish people at the oral entrance exam to the math department of Moscow State University. In fact, I have a whole page with a collection of such problems, called Jewish problems or Coffins. That page was one of the first pages I created when I started my website more than ten years ago.

When my son Alexey was in high school, I asked him to help me type these problems into a file and to recover their solutions from my more than laconic notes, and solve the problems that I didn’t have notes for. He did the job, but the file was lying dormant on my computer. Recently I resurrected the file and we prepared some of the solutions for a publication.

The problems that were given during these exams were very different in flavor: some were intentionally ambiguous questions, some were just plain hard, some had impossible premises. In our joint paper “Jewish Problems” we presented problems with a special flavor. These are problems that have a short and “simple” solution, that is nonetheless very difficult to find. This way the math department of MSU was better protected from appeals and complaints.

Try the following problem from our paper:

Find all real functions of real variable F(x) such that for any x and y the following inequality holds: F(x) − F(y) ≤ (x − y)².

I will give a talk on the subject for UMA at MIT on October 18, at 5pm.

What’s “plagiarism”? It’s when you take someone else’s work and claim it’s your own. It’s basically STEALING.

Ideas improve. The meaning of words participates in the improvement. Plagiarism is necessary. Progress implies it. It embraces an author’s phrase, makes use of his expressions, erases a false idea, and replaces it with the right idea.

Perhaps the Russians have done the right thing, after all, in abolishing copyright. It is well known that conscious and unconscious appropriation, borrowing, adapting, plagiarizing, and plain stealing are variously, and always have been, part and parcel of the process of artistic creation. The attempt to make sense out of copyright reaches its limit in folk song. For here is the illustration par excellence of the law of Plagiarism. The folk song is, by definition and, as far as we can tell, by reality, entirely a product of plagiarism.

If you copy from one author, it’s plagiarism. If you copy from two, it’s research.

In my essays The Oral Exam and A Math Exam’s Hidden Agenda, I gave some examples of math problems that were used during the entrance exams to Moscow State University. The problems were designed to prevent Jewish and other “undesirable” students from studying at the University. My readers might have supposed that an occasional bright student could, by solving all the problems, get in. Here is the story of my dear friend Mikhail (Misha) Lyubich; it shows that being extremely bright was not enough.

Misha passed the first three exams and was facing his last exam: oral physics. He answered all the questions. None of his answers were accepted: all of them were declared wrong. Misha insisted that he was right and requested that the examiners explain themselves. Every time their reply was the same:

This is not a consultation, it’s an exam.

Misha failed the exam. The solution to the last problem was a simple picture: a document that seemed to be impossible to deny, so Misha decided that he had grounds for an appeal. The person in charge denied the appeal. When Misha requested an explanation, can you guess the answer?

This is not a consultation, it’s an appeal.

Misha ended up studying at Kharkov State University. Now he is a professor at Stony Brook and the director of the Institute for Mathematical Sciences at Stony Brook.

You know that the negation of a true statement is a false statement, and the negation of a false statement is a true statement. You also know that you can negate a sentence by preceding it with “It is not true that ….”

Now look at the following statement and its negation, invented by David Bernstein. Which one is true?

• This sentence contains five words.
• It is not true that this sentence contains five words.

How about this pair?

• This sentence contains ten words.
• It is not true that this sentence contains ten words.