Vampires versus Mathematicians
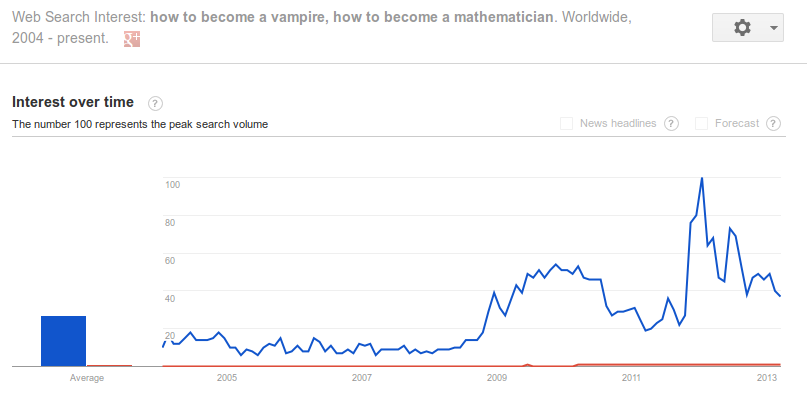
I just compared two searches on Google Trends:
- How to become a vampire is in blue.
- How to become a mathematician is in red.
Mathematics, applications of mathematics to life in general, and my life as a mathematician.
I just compared two searches on Google Trends:

The most personal puzzle that I wrote for the 2013 MIT Mystery Hunt was Integers and Sequences based on my Number Gossip database. I named it after the first lecture that I prepared after I decided to return to mathematics. It is still my most popular lecture.
Many of the clues in this puzzle are standard math problems that are very good for math competition training. Other clues are related to sequences and integer properties.
You might wonder why I often ask for the second largest integer with some property. Isn’t the largest one more interesting than the second largest? I do think that the largest number is more interesting, but exactly for this reason the largest number is available on my Number Gossip website and therefore is googleable. For example, my Number Gossip properties for 3000 contain the fact that 3000 is the largest palindrome in Roman numerals. This is why in the puzzle I used a slightly different clue, i.e. “the second largest three-letter palindrome in Roman numerals.”
It took me many hours to find non-googleable variations of interesting properties for this puzzle. Unfortunately, its non-googleability evaporated as soon as my solution was posted, right after the hunt. In any case some clues in this puzzle are useful for math competition training, and I plan to use them myself in my classes. The puzzle is attached below. I will post the solution in a couple of weeks.
*****
*****
*****
*****
*****
*****
*****
The ultimate goal of each MIT Mystery Hunt is to find a hidden coin. So it was highly appropriate that our 2013 team created a coin-weighing puzzle (written by Ben Buchwald, Darby Kimball, and Glenn Willen) as a final obstacle to finding the winning coin:
There are nine coins, one real and eight fake. Four of the fake coins weigh the same and are lighter than the real coin. The other four fake coins weigh the same and are heavier than the real coin. Find the real coin in seven weighings on the balance scale.
Actually, it is possible to find the real coin in six weighings. Can you do that?
Share:My weight used to be my most guarded secret. In general, I am a very open person: I’ll tell anyone anything about me, unless it involves other people. However, there were two exceptions, both of them numbers, interestingly enough: my age and my weight. The closest I came to revealing my weight was with my sister, because we often discuss our similar health issues. Unfortunately, she knows my age, so the only missing number is my weight. I am so tired of my struggle to lose weight, that I’ve stopped caring about keeping the number secret. I am ready to tell it to the whole world.
Let me start from the beginning. I grew up in a country and at a time when men liked plump women. I was never thin, and didn’t have to worry about my weight like my thin girlfriends did. I’ll never forget my high school boyfriend telling me, “Ninety percent of men like fat women, and the other ten percent like very fat women.” When in college I weighed 70 kilograms (154 pounds) and I felt fine. I had my first child when I was 23. I gained 20 kilos while I was breastfeeding, reaching 90 kilos (200 pounds). My husband Andrey kept telling me that he liked Rubenesque women. I wasn’t even slightly concerned about my weight. When we divorced in 1988, I felt that my world was crushed and I didn’t want to go on living. As a result, I lost about 20 pounds.
By 1990 I recovered from my depression, married my next husband, and moved to the US to live with him. The US made me aware of my weight immediately. It didn’t help that Andrey remarried a woman who was the opposite of Rubenesque. From this point on, I wanted to lose weight. After my second child was born, I gained 20 kilograms while breastfeeding, just as I had done with the first child. The result was that I weighed about 220 pounds, much more than I wanted.
I started to look around at what capitalist society had to offer. The pharmacy had many products. I tried Slim Fast, which started to kill my appetite immediately. However, I began to get depressed. The depression felt foreign. As a new mother, I had been very happy before using Slim Fast, and there had been no changes in my life other than consuming Slim Fast. I stopped using it and the depression disappeared. To make sure, I did an experiment. I started using Slim Fast again and the depression reappeared within three days. I stopped it and my depression disappeared. I was so desperate to lose weight that I repeated the experiment. But the result was the same. I stopped using it, and never used any slimming supplement since then. But within that whole process, I lost some weight.
I stayed slightly over 200 pounds for several years. The third time (after the divorce and the Slim Fast) that I lost a lot of weight was when I had my heart broken about 15 years ago. Since then I’ve been slowly gaining weight.
As you can see from my story, I was never able to lose weight when I wanted to. I lost it three times, but I can’t and don’t want to reproduce those circumstances. I actually do not know how to lose weight. For the past ten years I’ve been making changes in my eating habits that I hope, cumulatively, would help me lose weight. I do not buy soda or pizza. I significantly cut my consumption of sweets and starches. I eat more fruits and vegetables. I eat half of what I used to eat in a restaurant. I am still gaining weight.
he only thing I haven’t tried is to be hungry. I am afraid of being hungry. Also I am scared that if I decide on a plan which might result in my being hungry, I will not be able to stick to it. I don’t want to discover that I don’t have enough will power. I am scared to be a failure. I hope that by writing and publishing this I’ll gain the courage to replace my half-measures with a more drastic plan.
Oh! I forgot to tell you: I weigh 245 pounds.
Share:* * *
Grigori Perelman’s theorem: There is no offer you can’t refuse.
* * *
A conversation between two Russians:
— Run to the store and fetch a couple bottles of vodka.
— How much is a couple?
— Seven.
* * *
— Is it true that the Windows operating system was copied from a UFO computer that crashed in Roswell?
— All we know for sure is that the UFO that didn’t crash had a different operating system.
* * *
I saw our system administrator’s shopping list. The first line was tomatoes.zip for ketchup.
Share:I posted the puzzle In the Details two weeks ago. This is the most talked-about puzzle of the 2013 MIT Mystery Hunt. The author Derek Kisman invented this new type of puzzle and it is now called a Fractal Word Search. I anticipate that people will start inventing more puzzles of this type.
Let’s discuss the solution. The words in the given list are very non-random: they are related to fractals. How do fractals work in this puzzle? The grid shows many repeating two-by-two blocks. There are exactly 26 different blocks. This suggests that we can replace them by letters and get a grid that is smaller, for it contains one-fourth of the number of letters. How do we choose which letters represent which blocks? We expect to see LEVEL ONE in the first row as well as many other words from the list. This consideration should guide us into the matching between letters and the two-by-two blocks.
The level one grid contains 18 more words from the list. But where are the remaining words? So we have level one, and the initial grid is level two. The substitution rule allows us to replace letters by blocks and move from level one to level two. When we do this again, replacing letters in level two by blocks, we get the level three grid. From there we can continue on to further levels. There are three words from the list on level three and one word on level four. But this is quickly getting out of hand as the size of the grid grows.
Let’s step back and think about the next step in the puzzle. Usually in word search puzzles, after you cross out the letters in all the words you find, the remaining letters spell out a message. What would be the analogous procedure in the new setting of the fractal word search? In which of our grids should we cross out letters? I vote for grid number one. First, it is number one, and, second, we can assume that the author is not cruel and put the message into the simplest grid. We can cross-out the letters from words that we find in level one grid. But we also find words in other levels. Which letters in the level one grid should we cross out for the words that we find in other levels? There is a natural way to do this: each letter in a grid came from a letter in the previous level. So we can trace any letter on any level to its parent letter in the level one grid.
We didn’t find all the words on the list, but the missing words are buried deep in the fractal and each can have at most three parent letters. I leave to the reader to explain why this is so. Because there are so few extra letters, it is possible to figure out the secret message. This is what my son Sergei and his team Death from Above did. They uncovered the message before finding all the words. The message says: “SUM EACH WORD’S LEVEL. X MARKS SPOT.” Oh no! We do need to know each word’s level. Or do we? At this point, the extra letters provide locations of the missing words. In addition, if a word on a deep level has three parents, then it has to be a diagonal word passing through a corner of one of the child’s squares. So our knowledge of extra letters can help us locate the missing words faster.
Also, the message says that the answer to this puzzle will be on some level in the part of the grid that is a child of X. Luckily, but not surprisingly, there is only one letter X on level one. The child of X might be huge. But we could start looking in the center. Plus, we know from the number of blanks at the end of the puzzle, that the answer is a word of length 8. So Sergei and his team started looking for missing words and the answer in parallel. Then Sergei realized that the answer might be in the shape of X, so they started looking at different levels and found the answer before finding the last word on the list. The answer was hiding in the X shape in the center of the child of X on level 167: HUMPHREY.
H..Y .UE. .RM. H..PShare:
Cambridge Waldo puzzle from the 2013 MIT Mystery Hunt was supposed to be easy. Its goal was to get people out of the building for some fresh air. I made this puzzle jointly with Ben Buchwald, Adam (Pesto) Hesterberg, Yuri Lin, Eric Mannes and Casey McNamara. The puzzle consists of 50 pictures of different locations in Cambridge; one of the above individuals was hiding in each picture. Let me use this opportunity to thank my friends for starring in my puzzle and being inventive while doing it.
The puzzle starts with a group picture of my stars. The caption to the picture gives their names. The fact that they are standing in alphabetical order is a clue.
Out of the 50 pictures, each person appears in exactly ten pictures. If you mark the locations of one person on a map, they look like a letter. For example, below are Ben’s locations that form a letter “S”. When you put the letters in the alphabetical order by people names you get the answer to the puzzle: SCAMP.
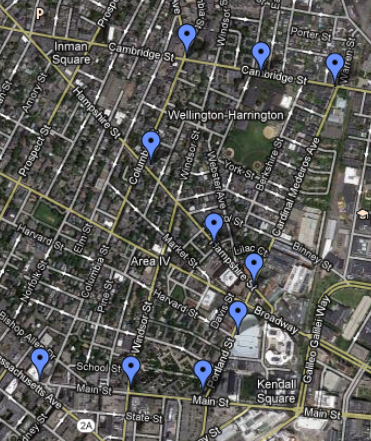
As you can see, you do not need all ten locations to recognize the letter. You might be able to recognize the letter with five locations, or at least significantly reduce possibilities for the letter. Besides, you do not need all the letters to recognize the answer. We thought that this was an easy puzzle.
And, to make it even easier, the order in which we posted the pictures was not completely random. The pictures of one person were in the order one might walk from one location to another. This played two important roles. If you recognize the person but do not recognize the location on the picture, you can make an approximate estimation of the location because it must be on the path between the previous and next locations. If you recognize the location but not the person, you can guess the person by checking whose path it fits better.
It was difficult to hide people, especially when there were no other people around. So we sometimes used props. We only used one prop per person. Here you can see Pesto with his sarongs in plain view. In the other picture (below) he is hiding under a white sarong. Yuri had a bicycle helmet. In one of the pictures, she hid so well that you couldn’t see her — but you could see her helmet. Ben had a bear hat. In one of the pictures you can only see a shadow of a person, but this person was clearly wearing a hat with bear ears. Eric didn’t have a prop, but my car was eager to make a cameo appearance at the Mystery Hunt, so I hid him in my car in one of the pictures.


As you might guess I made the pictures of different people at different times. So Ben Buchwald was the one who realized that solvers might differentiate people by looking at the data of the picture files. He carefully removed the original time stamps.
Despite our best intentions, our test-solvers decided not to leave their comfy chairs, but rather to use Google-StreetView. We strategically made some of the pictures not Google-StreetViewable, but our test-solvers still didn’t leave the comfort of their chairs. They just became more inventive. I do not know all the things they did to solve the puzzle, but I heard about the following methods:
I have yet to understand why this puzzle was difficult for the Mystery Hunt teams.
Share:Here is the solution to the Open Secrets puzzle I published recently. Through my discussion of this solution, you’ll also get some insight into how MIT Mystery Hunt puzzles are constructed in general.
I’ve included the puzzle (below) so that you can follow the solution. The puzzle looks like a bunch of different cipher texts. Even before we started constructing this puzzle, I could easily recognize the second, the seventh, and the last ciphers. The second is the cipher used by Edgar Allan Poe in his story, The Gold-Bug. The seventh cipher is a famous pigpen (Masonic) cipher, and the last is the dancing men cipher from a Sherlock Holmes story. Luckily you do not need to know all the ciphers to solve the puzzle. You can proceed with the ciphers you do know. With some googling and substitution you will translate these three pieces of text into: COLFERR, OAOSIS OF LIFEWATER, and RBOYAL ARCH.
These look like misspelled phrases, each of which has an extra letter. However, there are no typos in good puzzles. Or, more precisely, “typos” are important and often lead to the answer. So now I will retype the deciphered texts with the extra letter in bold: COLFERR, OAOSIS OF LIFEWATER and RBOYAL ARCH. In the first word it is not clear which R should be bold, but we will come back to that later.
At this point you should google the results. You may notice that the “royal arch” leads you to the Masons, who invented the pigpen cipher. From this, you can infer the structure of the ciphers and the connections among them. Indeed, a translation of one cipher refers to another. So you should proceed in trying to figure out what the texts you have already deciphered refer to. Eoin Colfer is the author of the Artemis Fowl series that contains a Gnomish cipher, and Oasis of Lifewater will lead you to Commander Keen video games with their own cipher. When you finish translating all of the ciphers, you get the following list:
The bold letters do not give you any meaningful words. So there is more to this puzzle and you need to keep looking. You will notice that the translations are in alphabetical order. This is a sign of a good puzzle where nothing is random. The alphabetical order means that you need to figure out the meaningful order.
To start, the phrases reference each other, so there is a cyclic order of reference. More importantly, the authors of the puzzle added an extra letter to each phrase. They could have put this letter anywhere in the phrase. As there is nothing random, and the placements are not the same, the index of the bold letter should provide information. If you look closely, you’ll see that the bold letters are almost all in different places. If we choose the second R in COLFERR as an extra R, then the bold letter in each text is in a different place. Try to order the phrases so that the bold letters are on the diagonal. You’ll see that this order coincides with the reference order, which gives you an extra confirmation that you are on the right track. So, let’s order:
Now the extra letters read BOKLORYFH. This is not yet meaningful, but what is this puzzle about? It is about famous substitution ciphers. The first and most famous substitution cipher is the Caesar cipher. So it is a good idea to use the Caesar cipher on the phrase BOKLORYFH. There is another hint in the puzzle that suggests using the Caesar cipher. Namely, there are many ways to clue the dancing men code. It could be Conan Doyle, Sherlock Holmes, and so on. For some reason the authors chose to use the word ELEMENTARY as a hint. Although this is a valid hint, you can’t help but wonder why the authors of the puzzle are not consistent with the hints. Again, there is nothing random, and the fact that the clues are under-constrained means there might be a message here. Indeed, the first letters read ROMAN CODE, hinting again at the Caesar shift. So you have to do the shift to arrive at the answer to this puzzle, which is ERNO RUBIK.

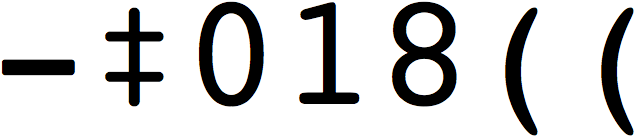
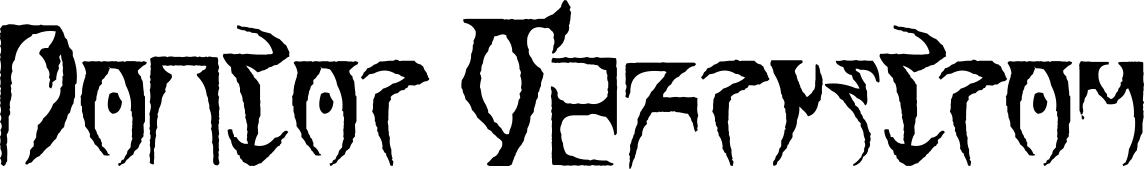





The most difficult puzzle I wrote for the MIT Mystery Hunt 2013 was Turnary Reasoning. I can’t take credit for the difficulty: I designed the checkers positions; they were expectedly the easiest. Timothy Chow created the chess positions, and Alan Deckelbaum created the MTG positions. As the name of the puzzle suggests, you need to find whose turn it is in each position or, as the flavor text suggests, decide that the position is impossible.
I tried to solve the chess positions myself and was charmed by their beauty. The most difficult one was the first chess puzzle presented below. Find whose turn it is or prove that the position is impossible.

The puzzle titled “50/50” was the most difficult puzzle in MIT Mystery Hunt 2013. It is a puzzle in which information is hidden in the probability distribution of coin flips. I consider it the most difficult puzzle of the hunt because it took the longest time to test-solve and we were not able to solve all four layers of the original puzzle. As a result, one of the layers was removed. I think this puzzle is very important and should be included in statistics books and taught in statistics classes. If I were ever to teach statistics, I would teach this puzzle. By the way, this elaborate monstrosity (meant as a compliment) was designed by Derek Kisman.
I am not sure that the puzzle is working on the MIT server. The puzzle is just a coin flip generator and gives you a bunch of Hs (heads) and Ts (tails). Here is the solution.
When you flip a coin, the first thing to check is the probability of heads. In this puzzle it is fifty percent as expected. Then you might check probabilities of different sequences of length 2 and so on. If you are not lazy, you will reach length 7 and discover something interesting: some strings of length seven are not as probable as expected. The two least probable strings are TTHHTTH and HTHHTTT, with almost the same probability. The two most probable strings are TTHHTTT and HTHHTTH, with the matching probability that is higher than expected. All oddly behaving strings of length 7 can be grouped in chunks of four with the same five flips in the middle. In my example above, the five middle flips are THHTT. Five flips is enough to encode a letter. The probabilities provide the ordering, so you can read a message. In the version I tested it was “TAXINUMBLOCKS.” In the current version it is “HARDYNUMBLOCKS.” Keep in mind that the message encoded this way has to have all different letters. So some awkwardness is expected. The message hints at number 1729, a famous taxicab number, which is a clue on what to do next in the second step.
What do you do with number 1729? You divide the data in blocks of 1729 and see how the k-th flip in one block correlates with the k-th flip in the next block. As expected, for most of the indices there is no correlation. But some of the indices do have correlation. These indices are close together: not more than 26 flips apart. Which means the differences will spell letters. Also, there is a natural way to find a starting point: the group of indices spans only a third of the block. In the original version the message was: “PLEASEHELPTRAPPEDINCOINFLIPPINGFACTORYJKHEREHAVEAPIECEOFPIE.”
Now I want to discuss the original version, because its solution is not available online. Here is Derek’s explanation of what happens in the third step:
So, this punny message is another hint. In fact the sequence of coin flips conceals pieces of the binary representation of Pi*e. These pieces are of length 14 (long enough to stand out if you know where to look, but not long enough to show up as significant similarities if you compare different sessions of flips), always followed by a mismatch. They occur every 1729 flips, immediately after the final position of the 1729-block message. The HERE in the message is intended to suggest looking there, but you can probably also find them (with more effort) if you search for matches with Pi*e’s digits.
The 14-flip sequences start near the beginning of the binary representation of Pi*e and continue to occur in order. (ie, every 1729 flips, 14 of them will be taken straight from Pi*e.) However, between sequences, either 1, 3, or 5 digits will be skipped. These lengths are a sequence of Morse code (1=dot, 3=dash, 5=letter break) that repeats endlessly, with two letter breaks in a row to indicate the start:
– …. ..- ..- ..- – ..- -..- ..- ..- ..- …. ..- …. – ..- ..- …. ..- ….
Translated, this gives the message “THUUUTUXUUUHUHTUUHUH”.
(Aside: I didn’t use Pi or e individually, because one of the first things I expect some teams will try is to compare the sequence of flips with those constants!)
As I said before, we didn’t solve the third step. So Derek simplified it. He replaced “PIECEOFPIE” by “BINARYPI”, and made it the digits of Pi, rather than of Pi*e. We still couldn’t solve it. So he changed the message from the second step to hint directly at the fourth step: “PLEASEHELPTRAPPEDINCOINFLIPPINGFACTORYJUSTKIDDINGTHUUUTUXUUUHUHTUUHUH.” But the binary Pi was still trapped in the coin flipping factory.
Here is Derek’s explanation of the fourth step:
Almost there! This message looks like some sort of flip sequence, because it has several Ts and Hs in there, but what of the Us and Xs? Well, U just stands for “unknown”, ie, we don’t care what goes there. And there’s only one X, so it seems significant!
The final step is to look for every occurrence of this pattern in the sequence. The flips that go where the X is are the final channel of information. You’ll find that they repeat in an unvarying pattern (no noise!) with period 323=17*19. There’s only one way to arrange this pattern into a rectangular image with a blank border, and it gives the following image:....................X..XXX.XXX.......X..X...X.X.......X..XXX.XXX.......X..X...XX........X..X...X.X.......X.....X..........X.....X..........X....XXX.........X.....X..........X................X.....XXX...X....X....XXXXX.XX...X....XX.XXXXX...X......XXXXXX....X...X.XXXXXXXX....XXX...XXXXX.XX..........XXX...X..................The final answer is the French word for fish, POISSON, a word heavily related to statistics!
The answer POISSON didn’t fit in the structure of the Hunt. So Derek was assigned a different answer: MOUNTAIN. He changed the picture and it is now available in the official solution to the puzzle. He adjusted his code for coin flips so that the picture of a mountain is hidden there. But the digits of Pi are still trapped in the flips. They are not needed for the solution, but they are still there.
Derek kindly sent to me his C++ program for the latest version of the puzzle. So if the MIT website can’t generate the flips, you can do it yourself. And play with them and study this amazing example of the use of statistics in a one-of-a-kind puzzle.
Share: