Tanya Khovanova's Math Blog

I have a leased Toyota Corolla, and I am happily enrolled in AutoCheck payments with Toyota’s Financial Services. So I do not even look at my bills. Once I opened my bill and noticed that the requested payment was twice as high as I expected. I looked closer and the bill had a car tax included in it. I looked even closer and read that:

Your Current Payment Due will be automatically withdrawn from your checking or savings account on the above Payment Due Date or the next banking day.

I decided that everything was taken care of and continued my relaxed life. After several months I checked my bill again, and the car tax was still there. After more careful study of my bill I discovered that Toyota’s “Current Payment Due” doesn’t include my car tax. Obviously they assume that their definition of “Current Payment Due” is crystal clear to everyone.

I got worried about this delayed car tax payment and went online to pay it. I tried to make this payment, but Toyota’s website rejected it. The website informed me that because I am enrolled in AutoCheck, I am not allowed to make separate online payments. I couldn’t believe it: to do so, I would have to de-enroll first!

So I just wrote a check.

In one day my feelings for my Toyota Corolla were turned around. If their financial system is designed so stupidly, what can we say about their car designs? Suddenly the sound of my brakes and the squeak in my steering wheel worry me.

I once wrote a story about a mistake that my medical insurance CIGNA made. They had a typo in the year of the end date of my insurance coverage in their system. As a result of this error, they mistakenly thought they had paid my doctors after my insurance had expired and tried to get their money back. While I was trying to correct all this mess, an interesting thing happened.

To help me explain, check out the following portion of my bill. (If it looks a bit funny, it’s because I cut out some details including the doctor’s name).

On the bill you can see that I had a mammography for which I was charged $493.00, but CIGNA paid only $295.80. The remaining $197.20 was removed from the bill as an adjustment, as frequently happens because of certain agreements between doctors and insurance companies. A year later when CIGNA made their mistake, they requested that the payment be returned. You can see on the bill that once the payment was reversed, my doctors reversed the adjustment too.

When CIGNA fixed the typo, they repaid the doctors, but the adjustment stayed on the bill, which the doctors then wanted me to pay. And that was only one of many such bills. It took me a year of phone calls to get the adjustments taken off, but this is not what I am writing about today.

If not for this mistake, I would have never seen these bills and the revealing information on the different amounts doctors charge to different parties, and how much they really expect to receive. As you can see my doctors wanted 67% more for my mammogram than they later agreed to.

The difference in numbers for my blood test was even more impressive. I was charged $173.00, and the insurance company paid $30.28 — almost six times less.

If I ever need a doctor and I don’t have insurance, I will take these bills with me to support my request for a discount. I do not mind if you use this article for the same purpose.

I met Ed (Edik) Frenkel 20 years ago at Harvard when he was a brilliant math student of my now ex-husband, and a handsome young man. Now, at 42, he is a math professor at Berkeley and he is even hotter. He made a bizarre move for a mathematician: he produced and starred in an erotic short movie, Rites of Love and Math. If he wants to be known as the sexiest male mathematician alive, he just might get the title.

The movie created a controversy when Mathematical Sciences Research Institute (MSRI) withdrew its sponsorship for the first screening after a lot of objections based on the trailer. My interest was piqued by a painting that dominated the visual of the trailer’s erotica scene. The black and white amateur painting is of the integral sign with Russian letters stylized as math symbols that spell the word “Truth”. In addition, the name of the woman in the movie, Mariko, means “truth” in Japanese. Though it felt pretentious, I was hoping that the movie would be symbolic. When I heard that the actors do not talk in the movie, my expectations of symbolism grew. I love movies that are open to interpretation. So I bought the movie, watched it and wrote the following review. Before getting to the review itself I would like to thank Ed Frenkel for sending me the photos and giving me permission to use them in my frank assessment of his work.

Here is the plot:

A Mathematician, hoping to serve humanity, discovers a formula of Love. Bad guys find an evil way to use the formula to destroy humanity and are hunting for the Mathematician, who is hiding in his lover Mariko’s home. The Mathematician fears for his own life. Although it would make sense to destroy all the papers with the formula, the Mathematician loves his formula even more than his lover and himself. He wants to preserve the formula and tattoos it on her body with her consent.

There is much about the film that I like, including the slow pace and the visuals, with their minimalistic background and palette of black, white and red. The camera work is superb.

I welcomed the idea of a Love formula, because mathematics is ready to broaden the scope of its models, including venturing into love. Of course, some mathematical models of relationships already exist.

It’s great that the mathematician is portrayed against the stereotype: he’s neither introverted nor asexual. Unfortunately, the movie plays into other stereotypes of male mathematicians — being creepy and demanding sacrifices from their wives in the name of mathematics. As I mentioned, I was looking forward to the movie, hoping that it would encourage the imagination of viewers in their interpretations. To my disappointment, every scene in the movie is preceded by text that describes the plot, removing any flexibility of interpretation. Besides that, the emotions portrayed didn’t quite match the written plot, in no small part because Ed Frenkel is not a good actor.

The idea of preserving a formula by tattooing it on someone is beyond strange. He could have used a safe-deposit box. Or put the formula in an envelope and given it to the lover to keep, or just encrypted it, etc. With narcissistic lack of consciousness, the Mathematician seems unaware of the implications of his action of imprinting this dangerous secret on Mariko. She can never go swimming, or go to the gym, or be intimate with anyone else. Moreover, if the bad guys discover that Mariko is the Mathematician’s lover, her life will be in grave danger. Not to mention that tattooing is painful.

Something that could have been interesting and watchable in a historic movie, in this contemporary movie seems pointlessly cruel, dehumanizing and senseless.

I know for sure that Ed Frenkel is not stupid, so what are his reasons for constructing the plot in this way? Before investigating his reasons, I have a mathematical complaint about the movie. Every mathematician and teacher knows that when asserting a formula you need to indicate its interpretation: what its symbols refer to in the real world. For example, suppose I tell you my own great Formula of Love: C_n = (2n)!/(n+1)!n!. You may recognize C_n as the Catalan numbers, but what does this have to do with Love? To give the formula meaning I need to tell you that C_n is the number of ways you can seat n loving couples at a round table with 2n chairs, so that each couple can join hands (assuming the arms are long enough to reach across the table) without any two pairs of arms crossing. Assigning an interpretation makes the Catalan numbers part of the world’s growing body of romantic research.

Writing a formula without mentioning what the variables mean fails to preserve it for the future. Ed Frenkel knows that. Wait a minute. The formula in the movie is actually not the Formula of Love, but a real formula from Ed’s paper on instantons. It’s right there, formula 5.7 on page 74. Every variable is explained in the paper. Ah-ha! So his movie isn’t actually about art, but rather about Ed’s formula. Indeed, there is no real Formula of Love. In such situations in other movies, they have simply shown fragments of a formula. However, in Rites of Love and Math, Frenkel’s formula — which has nothing to do with Love — is shot in full view, zooming in slowly.

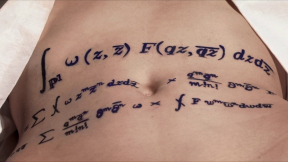
The movie is a commercial. Ed is using our fascination with sex to popularize his formula, and using his formula and his scientific standing to advertise his body.

I was so disappointed that the default interpretation of the movie was imposed on me by those pre-scene texts, that I decided to watch the movie for a second time, trying to ignore the text, hoping to find some new meaning.

If you decide to see the movie, you’ll probably come up with your own interpretation of the plot. I actually came up with several. I had a funny one and an allegorical one, but the most interesting task for me was to try create an interpretation matching the emotions portrayed:

Mariko knows that something is wrong in her sex life with the Mathematician. But she still loves him and writes him a love letter. The Mathematician comes to Mariko’s place. He is distant and cold. They cuddle. He explains to her that sex doesn’t bring him pleasure anymore and that moreover, he can’t even perform. He tells her that the only thing that brings him joy is mathematics and suggests that his sexual dysfunction and lack of pleasure will be fixed if they tattoo his favorite formula on her body. She agrees, but first they decide to give sex a last try. They try real hard. But he can’t relax and he doesn’t enjoy it, so she agrees to the tattoo. He does get excited during the tattooing process itself, but once he finishes his whole formula, he is no longer turned on. Mariko’s suffering has been in vain.

Darth Maul killed Qui-Gon Jinn. Obi-Wan Kenobi killed Darth Maul. Palpatine killed Mace Windu. Darth Vader killed Obi-Wan Kenobi and Palpatine. I am mentally drawing the kill graph of Star Wars, where people are vertices and kills are edges. The graph is not very interesting. In movies where no one gets resurrected, the kill graph is a forest.

I’m interested in studying social networks in the movies and how they differ from social networks in real life. As we saw, the kill graph is not very exciting mathematically.

Now let’s try the acquaintance graph, where edges mark two people who know each other. Unfortunately, in the movies there are often many nameless people and we learn very little about their acquaintances. On the other hand, all the “nameful” people usually know each other, thus their acquaintance graph is a complete graph. The richest acquaintance graphs would be for epic movies like Star Wars, in which the events span two generations and many planets. As a result, there are characters who never meet each other. For example, Leia, Luke and Han from the original trilogy never meet people who died in the prequel, such as Anakin’s mother and Count Dooku.

But I think that the most intriguing type of filmic social network is the fight graph, where edges represent characters who fight each other. Usually such graphs are bipartite, reflecting the division between bad guys and good guys. When an epic film is more complex and has traitors, the fight graph is no longer bipartite. Consider Darth Vader who fought and killed a lot of good guys including Obi-Wan Kenobi as well as many bad guys including Count Dooku and the Emperor.

I would like to immortalize Darth Vader in mathematics. He did restore the balance to the Force. If there is a graph which is not bipartite and can become bipartite by removing one highly connected node, I would like to name such a node Darth Vader.

Suppose Romeo is encouraged by love and attention. If Juliet likes him, his feelings for Juliet grow and flourish. If she doesn’t like him, he loses his interest in her.

Juliet, on the other hand, is the opposite. If Romeo doesn’t like her, she needs to win him over and her attraction for him grows. If he likes her, she feels that her task is accomplished and she loses her interest in him. Juliet likes the challenge more than the relationship.

Steven Strogatz used differential equations to model the dynamics of the relationship between Romeo and Juliet. This is a new and fascinating area of applied mathematical research; you can read more about the roller-coaster relationship between Romeo and Juliet in Steven Strogatz’s Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering.

Mathematicians like symmetry: in math literature they switch the roles between Romeo and Juliet randomly. So in some papers they give Romeo the role of preferring a challenge over love and in some papers they give that role to Juliet.

When I teach this subject of love, Alexander Pushkin’s famous quote always pops into my mind. The quote comes from the first lines of Chapter Four of Eugene Onegin, and in Russian it is:

Чем меньше женщину мы любим,
Тем легче нравимся мы ей…

I didn’t like the English translations that I found, so I asked my son Alexey to provide a more literal translation:

The less we love a woman, the more she likes us in return…

I blame Pushkin for my tendency to always pick Juliet as the character who thrives on the challenge, even though men are often assumed to be the chasers. I’d like to ask my readers to comment on these roles: Do you think both genders play these roles equally? If not, then who is more prone to be into the chase?

Let’s return to mathematical models. In the original model, the reactions of Romeo and Juliet are a linear function of feelings towards them. I would like to suggest two other roles, in which people react to the absolute value of feelings towards them. They do not care if it is love or hate: they care about intensity.

First, there is the person, like my friend Connie, who feeds on the emotions of other people. She’s turned on by guys who love her as well as by guys who hate her. If they’re indifferent, she’s turned off.

Second, there is the opposite type, like my colleagues George, Joseph, David and many others. They hate emotion and prefer not to be involved. They lose all interest in people who feel strongly about them and they like people who are distant. I know the name for this role: it’s a mathematician!

 I love the TV series of Angel and of Buffy the Vampire Slayer. I enjoy the excitement of saving the world every 42 minutes. But as a scientist I keep asking myself a lot of questions.

Where do vampires take their energy from? Usually oxygen is the fuel for the muscles of living organisms, but vampires do not breathe. Vampires are not living organisms, and yet they have to get their energy from somewhere.

When you kill a vampire, it turns to dust. If organisms are 60% water, then a 200-pound vampire should generate 80 pounds of dust. So why, in the series, do you get just a little puff of dust whenever someone plunges a stake into a vampire? Plus 120 pounds of water apparently evaporates instantly during staking. Can someone who is less lazy than me please calculate the energy needed to evaporate 120 pounds of water in one second? Because my first reaction is that you would need an explosion, not just one stab with Buffy’s stake.

All these unscientific elements do not actually bother me that much. What does bother me are inconsistencies in logic. For example, at the end of Season One of Buffy, Angel refuses to give Buffy CPR, claiming that as a vampire he can’t breathe. But then how can Spike and other vampires smoke? If they can smoke that means they are capable of inhaling and exhaling. Not to mention that these vampires talk: wouldn’t they need an airflow through their throats to produce sounds?

It would make more sense for the show to state that vampires do not need to breathe, but are nonetheless capable of inhaling and exhaling. So Angel should have given Buffy CPR. It would have created a great plot twist: Angel saves Buffy at the end of Season One, only for her to send him to the hell dimension at the end of Season Two.

Back to breathing. I remember a scene in “Bring On the Night” in which Spike was tortured by Turok-Han holding his head in water. But if Spike can’t breathe, why is this torture?

Another thing that bothers me in the series is not related to what happens but to what doesn’t happen. For example, vampires do not have reflections. So I don’t understand why every vampire-aware person didn’t install a mirror on the front door of their house to check for reflections before inviting anyone in.

Also, it looks like producers do not care about backwards compatibility. Later in the series we get to know that vampires are cold. Watch the first season of Buffy with that knowledge. In the very first episode, Darla is holding hands with her victim, but he doesn’t notice that she is cold. Later Buffy kisses Angel, before she knows that he is a vampire, and she doesn’t notice that he’s cold either. Unfortunately, the series also isn’t forward compatible. In the second season of Angel in the episode “Disharmony”, when we already know that vampires are cold, Harmony is trying to reconnect with Cordelia. They hug and touch each other. Such an experienced demon fighter as Cordelia should have noticed that Harmony is cold and, therefore, dead.

Finally, let’s look at Spike in the last season of Angel. Spike is non-corporeal for a part of the season; we see him going through walls and standing in the middle of a desk. Yet, one time we see him sitting on a couch talking to Angel. In addition, he can take the stairs. He can go through the elevator wall to ride in an elevator instead of falling down through its floor. And what about floors? Why isn’t he falling through floors? Some friends of mine said that we can assume that floors are made from stronger materials. But, if there is a material that can prevent Spike from penetrating it, they ought to use this material to make a weapon for him.

I’ve never been involved in making a show, but these producers clearly need help. Perhaps they should hire a mathematician like me with an eye for detail to prevent so many goofs.

Silvio Micali taught me cryptography. To explain one-way functions, he gave the following example of encryption. Alice and Bob procure the same edition of the white pages book for a particular town, say Cambridge. For each letter Alice wants to encrypt, she finds a person in the book whose last name starts with this letter and uses his/her phone number as the encryption of that letter.

To decrypt the message Bob has to read through the whole book to find all the numbers. The decryption will take a lot more time than the encryption. If the book increases in size the time it takes Alice to do the encryption almost doesn’t increase, but the decryption process becomes more and more draining.

This example is very good for teaching one-way functions to non-mathematicians. Unfortunately, the technology changes and the example that Micali taught me fifteen years ago isn’t so cute anymore. Indeed you can do a reverse look-up online of every phone number in the white pages.

I still use this example, with an assumption that there is no reverse look-up. I recently taught it to my AMSA students. And one of my 8th graders said, “If I were Bob, I would just call all the phone numbers and ask their last names.”

In the fifteen years since I’ve been using this example, this idea never occurred to me. I am very shy so it would never enter my mind to call a stranger and ask for their last name. My student made me realize that my own personality affected my mathematical inventiveness.

Since modern technology is murdering my 15-year-old example, I would like to ask my readers to suggest other simple examples of one-way functions or ways to resurrect the white pages example.

I received a message at the beginning of October: “This month has 5 Fridays, 5 Saturdays and 5 Sundays; this only happens every 823 years.”

Wait a minute. The Gregorian calendar cycles every 400 years. Where is the figure of 823 coming from?

Wait another minute. Within a century the calendar repeats itself every 28 years. So we are guaranteed that October 2038 will be the same as October 2010.

Wait one more minute. To have a month with five Fridays, Saturdays and Sundays, we need a month that has 31 days and starts on a Friday. There are seven months a year with 31 days, so on average we would expect to have such a month once a year.

If you study the calendar you can see that the seven long months start on six different days. This means that two of the months start on the same day and one of the days is skipped altogether. We see this in both leap years and non-leap years.

Ironically, 2010 is the year with two long months starting on Friday — October and January. Despite the claims of the email about this only happening every 823 years, in fact the same phenomenon occurred twice this year. The next time this will happen is in July 2011.

For those people who get all excited when a month has five Fridays, five Saturdays and five Sundays, I have good news for you. The month following each of these months has to start on Monday. And unless it is a February of a non-leap year, it will have five Mondays.

In 2009 I was working at MIT coordinating math research for Research Science Institute for high school students. One of our students Jacob Hurwitz got a project on decycling graphs.

“Decycling” means removing vertices of a graph, so that the resulting graph doesn’t have cycles. The decycling number of a graph is the smallest number of vertices you need to remove.

Decycling is equivalent to finding induced forests in a graph. The set of vertices of the largest induced forest is a complement to the smallest set of vertices you need to remove for decycling.

Among other things, Jacob found induced trees and forests of the highest densities on graphs of all semi-regular tessellations. On the pictures he provided for this essay, you can see an example of a tessellation, a corresponding densest forest, and a corresponding densest tree. The density of the forest and the tree is 2/3, meaning that 1/3 of the vertices are removed.

To motivate RSI students I tried to come up with practical uses for their projects. When I was talking to Jacob about decycling, the only thing I could think of was terrorists. When terrorists create their cells, they need to limit connections among themselves, in order to limit the damage to everyone else in the cell if one of them gets busted.

That means the graph of connections of a terrorist cell is a tree. Suppose there is a group of people that we suspect, and we know the graph of their contacts, then the decycling number of the graph is the number of people that are guaranteed to be innocent.

Have you noticed how Facebook and LinkedIn are reasonably good at suggesting people you might know? The algorithm they use to analyze the data is fairly effective in revealing potential connections. Recently, someone was able to download all of the Facebook data, which means that any government agency ought to be able to do the same thing. They could analyze such data to discover implicit connections. As a byproduct of looking for terrorists, they would also discover all of our grudges.

Oh dear. What are they going to think when they find out I’m not connected to my exes?

I am a milk person. I can easily drink half a gallon of milk a day. The problem with half a gallon of milk a day is that it is about half of my target calorie intake. That is why I switched to the reduced-fat milk. It didn’t taste good, but I was very proud of myself. That is, I was proud for about a year until I finally decided to read the labels. One serving of whole milk is 150 calories, while one serving of reduced-fat milk is 130 calories. All this year-long suffering saved me an insignificant 13%. Not to mention that the amount of sugar is the same.

I decided to look into this more closely. I went to my nearest super-market and checked the milk. The low-fat milk is 110 calories per serving, while non-fat milk is 90 calories.

If I had just reduced my milk intake by half, I would have consumed fewer calories than by replacing whole milk with non-fat milk, but I would have enjoyed it so much more. The lesson? Read the labels and do the math!