The Game of SET for Groups (Part 1), jointly with Andrey Khesin
The deck for the game of SET consists of 81 cards. Each card has 1, 2, or 3 identical objects. Each object is an oval, a diamond, or a squiggly, colored in red, green, or purple, and the shading can be solid, striped, or empty. Three cards form a set if, for each feature (number, shape, color, shading), all three are either the same or all different. For example, one red striped squiggly, two red striped ovals, and three red striped diamonds form a set. The numbers are all different (1, 2, and 3); the shapes are all different (squiggly, oval, diamond); the color is the same (red), and the shading is the same (stripped). Another example of a set with all features different is shown in the picture.

For every feature, we can assign values of 0, 1, 2, modulo 3. The fact that the values are the same or all different is equivalent to saying that the values sum up to zero modulo 3. Thus, we can view the cards as points in a 4D vector space over the field F3, namely F34. Three cards form a set if and only if the corresponding vectors sum up to the zero vector. Sets have a very useful property: for any two cards in a deck, there exists a third card that completes the given two cards to a set.
Before we generalize the game of SET, let’s talk about notation. Above, we looked at the values we assign for one feature as the field F3. If we want to talk about vectors, since technically a vector space must be over a field, we could use this definition. However we do not use its multiplicative properties, so we can say that values for one attribute are in Z3. If we want to forget about the exact values, and just use the group structure, we can use notation C3.
Let’s see in what ways we can extend this definition. People have tried to generalize the game of SET to a group. Suppose each card corresponds to an element in a group. Then, we want to arrange three cards so that the corresponding three elements multiply to the identity. If the group is non-commutative, then the order matters. That means the players do not just pick out the three cards, they have to arrange them in a line so that the corresponding product is the identity. However, we still retain a useful property. If our card deck contains all possible elements of the group, then for any two cards in a given order, there exists a card that completes them to a set so that the product is the identity. However, another problem is that this card might be one of the cards we already have. On the plus side, we can rearrange the order of the cards, getting more options. We can also say that a set can consist of any number of cards, not just 3, as long as the product is the identity.
The Numberphile video The Game of Set (and some variations) shows examples of such games. One of the decks they show represents the group S3: permutations of 3 elements. The picture shows a screenshot from the video with a set in a different group, but if you ignore the blue beads, you will get a set in S3. The red dots at the bottom mark odd permutations. This helps see sets faster: each set has to have an even number of red dots. This deck is a toy example of what is possible with only 6 elements in the group.
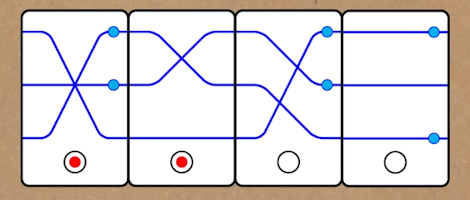
They also show a similar deck corresponding to group S4: permutations of 4 elements. Thus, the deck size is 24. Despite the size not being very big, the video claims that the game is tough to play. One more deck represents two permutations of 3 elements, and one must get to the identity on both of them. Thus, the deck size is 36, and the underlying group is S32. These games are sometimes called Non-abelian sets. A third deck is a deck with three crossing lines with beads. The crossing lines correspond to permutations of three elements, and each string either has a bead or not. To get to the identity, you need an even number of beads on each line. Thus, the deck size is 48 and corresponds to the group that is called the wreath product of C2 and S3, where Cn is the cyclic group with n elements. The wreath product is used because a copy of C2, each of the beads, is associated with each of the three lines that the first group, S3, is acting on.
The screenshot from the video we mentioned corresponds to this group, showing four cards forming a set. The red dot at the bottom signals the parity of a permutation, and there has to be an even number of them, but you can ignore them. However, the meaningful dots are small blue dots on some lines, and there has to be an even number of them on each line.
In practice, one card in each deck will contain the group identity, so this card is typically removed from such games. Leaving it in would allow anyone to add it to any other set they found, getting a free point (if the score is the number of cards for each set). Thus, the actual deck size contains 1 fewer card than the corresponding group.
One famous example of such an extension of SET that wasn’t shown in the Numberfile video is often called “ProSet” (short for Projective Set). It is usually marketed under other names, for example, “Socks”. It is played on the group F26 with the identity card removed, making the deck 63 cards. The cards each contain some non-empty subset of 6 colored dots/socks. A set is any group of cards where each color appears an even number of times. This is equivalent to adding vectors in F26 and having them add to the identity: the zero vector. Since the group operation is addition, which is commutative, the sets found do not need to be in a particular order. The picture shows a set in the game of Socks.
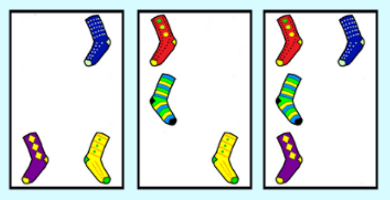
However, there is a fundamental difference between the classic game of SET and the extensions we have talked about. No card in the SET deck obviously corresponded to the identity and had to be removed. It is almost as if the SET group “forgot” about its identity element. A group that has “forgotten” about its identity can be informally called a torsor. A torsor has a more sophisticated definition, but this casual one will do for our purposes. We also note that SET sets always contain exactly three cards. The sets have the following property: if we had chosen a particular assignment of the values of 0, 1, and 2 to each property, as in the Numberphile video, we would find that changing this assignment would have the following effect: if the initial set has all attributes different, the set will not change; if the attributes are all the same, each value would be shifted by the same shift s. The sum would thus be shifted by 3s = 0, as we look at everything mod 3.
Another affine game is a game of EvenQuads played on a deck of size 64. Each card has 3 attributes with 4 values each. Each card has symbols of a color (red, yellow, green, or blue), a shape (spiral, polyhedron, circle, square), and a quantity (from 1 to 4). The set, called quad in this game, consists of four cards such that for each feature, one of three things is true: 1) all of the cards are the same, 2) all of the cards are different, and 3) the card’s values are divided fifty-fifty. The picture shows the set in this game.

Can we extend the notion of a torsor to ProSet? The answer is yes! EvenQuads is almost equivalent to the game of ProSet: you just need to pick the card corresponding to the origin and only allow sets with four cards. The four values of each attribute in EvenQuads represent all possible values of 2 different socks in ProSet/Socks. With 3 attributes, we can express all possible values of 6 dots/socks. This is more restrictive than the set that we could choose in ProSet, but the advantage is that our deck is now completely free of a choice of a particular identity value. ProSet can be used to play EvenQuads and vice versa (with the exception of the identity card); the “torsor-ness” of EvenQuads makes the definition of a set cleaner. Indeed, a set in EvenQuads is not any set of cards that forms a set in ProSet. See more about how different famous card games are equivalent to each other in the paper Card Games Unveiled: Exploring the Underlying Linear Algebra.
At this point, it is worth noting that nothing about the games of SET, ProSet, or EvenQuads requires the exact dimension chosen. The game of SET uses C3 as an underlying group and chooses to use 4 copies of it. Both ProSet and EvenQuads use 6 copies of C2. The choice of dimension, the number of copies, is usually made with practical considerations in mind to make the number of cards in the deck, 81 and 64, respectively, to be of a reasonable quantity. However, to design a new game, we only have to verify that the underlying group is satisfactory, and only then do we need to fix a dimension.
So, how would we generalize further? If each attribute was an element of Z4 instead of Z22, would that work? Recall that in the game of SET, we require three cards to sum to zero in Z32. In ProSet and EvenQuads, we also require the cards to sum to zero in Z26, where in ProSet, we use any number of cards, and in EvenQuads, we use four cards. Coming back to Z4, suppose we announce that x cards form a set if their sum is zero. If we want the cards that are all the same in each feature to form a set, we need x to be divisible by 4. If we choose x to be 4, we will lose the ability to select “all different” as a valid combination of attributes since 0+1+2+3 = 2 mod 4. Any other x that is divisible by 4 is too big to play. And in any case, we lose symmetry between different values. For example, when the attributes are divided fifty-fifty, sometimes they sum to zero, as in 1+1+3+3, and sometimes not, as in 1+1+2+2.
Is this it? Should we stop there? Let’s not. Let’s check Z5. To allow all cards to be the same, we will claim that sets must have 5 cards. The good news is that 0+1+2+3+4 = 0 mod 5. Suppose we define the set as 5 cards that sum to zero modulo 5. The big question is, can we define the rule without assigning the exact values to each attribute? Let’s look at an example of a set: 0,0,0,2,3. We can’t claim a set to be three of the same values, and two others are different. However, if we specify a relative order of our elements and allow 0,0,0,2,3 to be a set, then together with it, all shifted sequences correspond to a set; for example, shifting by 1 produces 1,1,1,3,4.
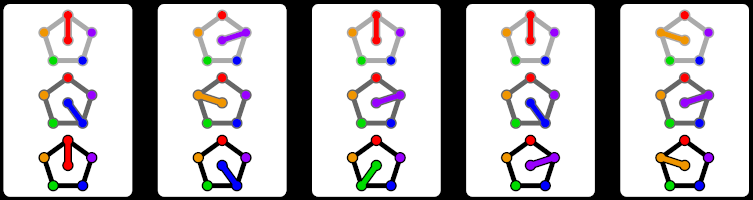
In particular, to make a game based on Z5, we can demand that our sets consist of 5 cards that add to the identity. The fact that each set has 5 cards means that we can use a torsor and do not need to explicitly specify the identity. If we represent our 5 attributes as points on a pentagon or lines pointing in one of 5 directions, we observe a remarkable pattern: the 5 values add to 0 exactly when there is a line of symmetry in the chosen attributes! Below, we see all possible ways to add 5 values mod 5 and arrive at 0, up to rotations. As an example, if we chose 3+2+1+2+2=0 mod 5, we would see that this corresponds to the second symmetry in the picture, which we can view as drawing an axis of symmetry “through the 2”.

This is a property unique to the number 5, and also for numbers smaller than 4. This is not true for larger sizes of groups; for example, 0+0+0+1+2+3=6 has no symmetries in Z6. Number 4 represents an interesting case. If we represent our 4 attributes as points on a square or lines pointing in one of 4 directions, we observe that when the 4 values add to 0, there is a line of symmetry in the chosen attributes. However, in the case of values 0, 0, 3, 3, or, 0, 1, 2, 3, there is a line of symmetry, but the values do not sum to zero.
So we have shown that a torsor of C5, the cyclic group of 5 elements, might make for a convenient group on which to play a variant of SET. A reasonable choice of dimension might be 3, making a deck of size 125. This game would then be played on a C53-torsor. This inspired the name of this game as, this has been shortened to C53T, pronounced “C-Set”. To illustrate a card, we use pentagons with an indicated vertex to denote an element of C5. We need 3 pentagons, one for each dimension. To help players work around the fact that cards often get turned around, each direction on each pentagon is assigned a color to help players tell them apart better. Additionally, the three pentagons are shaded to clarify which pentagon corresponds to each dimension. In the image below, we see a C53T set, where the symmetric axes in each of the three dimensions go through the red, orange, and “any” axes from top to bottom.
This and many other games can be found on tsetse website. The website has a description, and also allows for a solitaire play.
Finding sets in C53T is extremely hard, so this is not a game for casual players, but it does serve to illustrate what really makes a set a set. In everything discussed in this blog post, we either used a group with a clear identity (such as in the Numberphile video) or a commutative operation (such as in C53T). Is there any way to have a non-abelian group torsor to play a variant of SET? The answer is yes, but that is a story for another day.
Share:



