Pass-Fail
Recent Facebook Puzzle from Denis Afrisonov.
Share:Puzzle. 100 students took a test where each was asked the same question: “How many out of 100 students will get a ‘pass’ grade after the test?” Each student must reply with an integer. Immediately after each answer, the teacher announced whether the current student passed or failed based on their answer. After the test, an inspector checks if any student provided a correct answer but was marked as failed. If so, the teacher is dismissed, and all students receive a passing grade. Otherwise, the grades remain unchanged. Can the students devise a strategy beforehand to ensure all of them pass?
My Favorite Shoes
(A small piece I wrote on Dec 29, 2009. Edited in 2024.)
They were black, very comfy, and felt like a second skin. The shoes had this shock-absorbing cushioning, so asphalt felt like carpet.
I had them for 10 years. They served me for so long that I started believing our happy relationship would last forever.
First, I noticed that they are not black anymore. They acquired a greenish color. Then, the sound changed. Steps started sounding like farts. I trusted my shoes so much that, at first, I thought I was just getting old. But I realized that I couldn’t be that perfect: I couldn’t possibly fart with such a precise rhythm. Besides, I should have run out of gas from time to time.
When I came home, I took off my shoes and looked at them. The sole of one shoe was gone. My love affair with my shoes was over. Oh well. The divorce was easy. They went to my garbage can. No tears, no broken hearts, just a lost sole.
Share:Another Symmetry Puzzle
I recently posted a symmetry puzzle from Donald Bell. He just sent me another one.
Puzzle. Start with a 30-60-90 triangle (half of an equilateral triangle). Divide it into two 30-60-90 triangles of different sizes by dropping a perpendicular from the right-angled corner to the opposite side. Put the resulting two pieces together to form a symmetrical shape. There are two solutions.
It took me some time to find the second solution. I love this puzzle.
Share:
Is It Possible?
Usually, I only post puzzles to which I know the solution. However, I don’t know the solution to this exciting geometry question from Facebook, yet. But I like the puzzle so much that I’d rather post it than wait until I find time to think about it.
Puzzle. A centrally-symmetric figure is cut into two equal polygons: A and B. Is it possible that the center of symmetry is in A but not in B?
Share:
An Alternator Coin Puzzle
I run a program at MIT called PRIMES STEP, where we conduct mathematical research with children in grades 6 through 9. Our first research project was about a funny coin called an alternator. This coin exists only in a mathematician’s mind as it can change weight according to its own will. When you put the alternator on the scale, it can either weigh the same as a real coin or a fake coin (the fake coins are lighter than real ones). The coin strictly alternates how much it weighs each time it is put on the scale. My colleague, Konstantin Knop, recently sent me a fresh alternator puzzle.
Puzzle. There are four identical-looking coins: two real, one fake, and one alternator. How do you find the alternator using a balance scale at most three times?
Share:
2024 MIT Mystery Hunt
I am not as excited about the MIT Mystery Hunt as I used to be. So, for this year’s hunt, I didn’t go through all the puzzles but present here only the puzzles that were recommended to me. I start with math, logic, and CS.
- Scan, a bunch of numbers. The puzzle requires some programming.
- Flamingo, several grids that look like Nikoli puzzles.
- Jigsaw Slitherlink.
- Under Pressure, evaluating equations.
Then we have some word puzzles.
- Deposit at the Word Bank.
- Body Language, a crossword.
- Fren Amis, a crossword in many languages.
- Look Before You Leap, a crossword with seemingly meaningless clues.
Now, the rest.
- Queen Marchesa to g4 starts with a Magic-the-Gathering card showing a chess piece: white queen.
- New Rules, weird sentences about games.
- Itineratum de Urbes Universum, looks like Latin.
- Retro Chess Puzzle.
Calculus in Life
Here is an old joke.
A former student runs into an old calculus teacher as she is shuffling home. The student is happy to see her and says, “I recently thought about you and our classes.” “How so?” she perks up. “I was in a bit of a pickle when calculus helped me,” he says. The old lady straightens, and her face begins to glow. “Can you elaborate?”, asks the teacher in anticipation. The student proceeds with his story. “I was walking home in the pouring rain when a gust of wind snatched my hat right off my head. The hat landed in a puddle. This wasn’t just any hat; it was a gift from my dad, so I really wanted to get it back. But I didn’t exactly fancy diving headfirst into the puddle. So, I looked around and saw a piece of wire. I bent it into the shape of an integral and used it to fetch my hat.”
Share:Tesseracts and Foams
Foams are a recent craze in homology theory. I want to explain what a foam is using a tesseract as an example. Specifically, the 2D skeleton of a tesseract is a foam.
We can view a tesseract as a convex hull of 16 points in 4D space with coordinates that are either 0 or 1. The edges connect two vertices with the same three out of four coordinates. Faces are squares with corners being four vertices that all share two out of four coordinates.
Foam definition. A foam is a finite 2-dimensional CW-complex. Each point’s neighborhood must be homeomorphic to one of the three objects below.
- An open disc. Such points are called regular points.
- The product of a tripod and an open interval. Such points are called seam points.
- The cone over the 1D-skeleton of a tetrahedron. Such points are called singular vertices.
My favorite example of a foam is a tesseract. Or, more precisely, the set of tesseract’s vertices, edges, and faces form a foam.
- The regular points are the insides of the tesseract’s faces. Their neighborhoods are obviously open discs.
- The seam points are the insides of the tesseract’s edges. Each edge is incident to three faces, and the projection of its neighborhood to a plane perpendicular to the edge is a tripod.
- The singular vertices are the tesseract’s vertices. Each vertex is incident to four edges and six faces. We can view this neighborhood as a cone cover of a tetrahedron formed by this vertex’s neighbors.
Some of the coolest foams are tricolorable. A foam is called tricolorable if we can color it using three colors in such a way that each face has its own color, and any three faces that meet at a seam are three distinct colors.
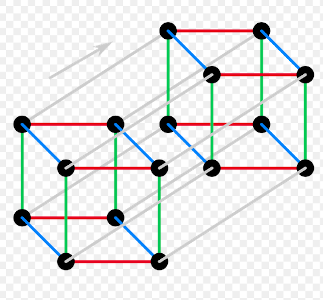
Not surprisingly, I chose a tricolorable foam for our example. Let me prove that the tesseract’s 2D skeleton is tricolorable. We start by coloring the edges in four colors depending on the direction: red, green, blue, or gray, as in the first picture (source: Wikipedia). Each face has two pairs of edges of two different colors. We can color the faces in the following manner: if none of the edges are gray, then the face color is the complementary non-gray color (For example, if the edges are red and blue, the face is green). If the edges are gray and one other color, then the face color matches the non-gray color (For example, if the edges are red and gray, the face is red). I leave it to the reader to prove that this coloring means that each edge is the meeting point of three different face colors.
Here is an interesting property of tricolorable foams. It is Proposition 2.2 in the paper Foam Evaluation and Kronheimer-Mrowka Theories, by Mikhail Khovanov and Louis-Hardien Robert.
Proposition. If we remove the regular points of one particular color from a tricolored foam, we will get a closed compact surface containing all the seam points and singular vertices.

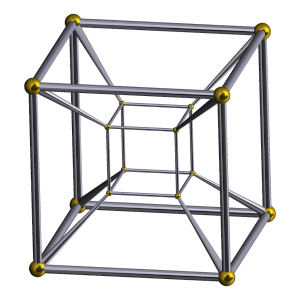
In our example, the result is a torus, which you can recognize in the second picture. Here, I use the Schlegel diagram as a model for a tesseract, shown on the right (source: Wikipedia). The exercise for the reader is to explain where the eight green faces of the torus were before they were removed.
The following lemma from the aforementioned paper describes another cool property of a tricolorable foam.
Lemma. If a foam is tricolorable, its 1D skeleton (the graph formed by seams and singular points) is bipartite.
And, surely, I am leaving it up to the reader to check that the tesseract’s 1D skeleton forms a bipartite graph.
Share:
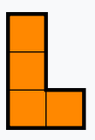
Three L-tetraminoes
Here is a cool puzzle I heard from Tiago Hirth at the last Gathering for Gardner, who in turn heard it from Donald Bell.
Puzzle. You have three L-tetrominoes. Arrange them on a plane without overlaps so that the resulting shape has a line of symmetry.


Share:
