Tanya Khovanova's Math Blog

One of the perks of being a teacher is receiving congratulations not only from family and friends, but also from students. By the way, I do not like physical gifts — I prefer just congratulations. Luckily, MIT has a policy that doesn’t allow accepting gifts of any monetary value from minors and their parents.

Thus, my students are limited to emails and greeting cards.

One of my former students, Evin Liang, got really creative. He programmed the Game of Life to generate a Christmas card for me. You can see it for yourself on YouTube at: Conway Game of Life by Evin Liang.

This is one of my favorite congratulations ever.

Puzzle. There are 100 cards with integers from 1 to 100. You have three possible scenarios: you pick 18, 19, or 20 cards at random. For each scenario, you need to estimate the probability that the sum of the cards is even. You do not need to do the exact calculation; you just need to say whether the probability is less than, equal to, or more than 1/2.

I like including warm-up puzzles with every homework.

Puzzle. Farmer Giles has four sheep. One day, he notices that they are all standing the same distance away from each other. How can this be so?

The expected answer: The configuration is impossible in 2D. So, one of the sheep is on a hill or in a pit.

Some students thought big: The sheep could be placed at different locations around the Earth, forming a really big tetrahedron. In this case, we need to explain what it means for the farmer to “notice”, but this minor issue could be resolved in many ways.

Some of the students questioned the meaning of the word distance. They argued that if sheep are all touching each other, they are the same distance 0 from each other. One way this could happen is if the tails of the four sheep were entangled.

I loved coin puzzles, but after several research projects related to those shiny discs, I got tired of them. The fatigue was temporary, as confirmed by the following Facebook puzzle that reignited my interest.

Puzzle. There are 30 coins in a circle that look the same. However, 20 of them are fake, and the rest are real. Fake coins weigh the same, and real coins weigh the same but heavier than fake ones. You need to find as many fake coins as possible using a balance scale once, given that the fake coins are positioned consecutively. What is your strategy?

My PRIMES STEP program consists of two groups of ten students each: the senior group and the junior group. The senior group is usually stronger, and they were especially productive last academic year. We wrote four papers, which I described in the post EvenQuads at PRIMES STEP. The junior group wrote one paper related to the game SOS. The game was introduced in the following 1999 USAMO problem.

Problem. The game is played on a 1-by-2000 grid. Two players take turns writing an S or an O in an empty square. The first player who produces three consecutive squares that spell SOS wins. The game is a draw if all squares are filled without producing SOS. Prove that the second player has a winning strategy.

The solution is quite pretty, so I do not want to spoil it. If my readers want it, the solution for this grid, and, more generally, for any grid of size 1-by-n, is posted in many places.

My students studied generalizations of this game, and the results are posted at the arXiv: SOS. We tried different target strings and showed that:

• The SOO game is always a draw.
• The SSS game is always a draw.
• The SOSO game is always a draw.

Then, we tried a version where the winner needed to spell one of two target strings. We showed that:

• The SSSS-OOOO game is always a draw.

We tried several more elaborate variations, but I want to keep this post short.

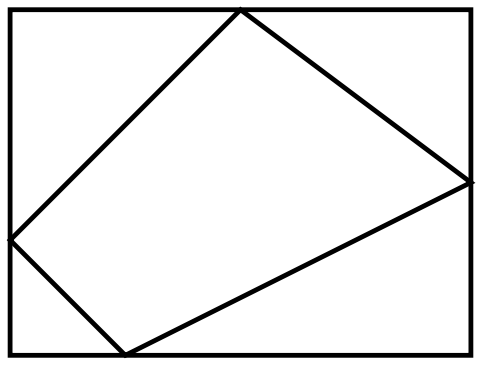
I recently posted A Quadrilateral in a Rectangle puzzle.

Puzzle. A convex quadrilateral is inscribed in a rectangle with exactly one quadrilateral’s vertex on each side of the rectangle. Prove that the area of the rectangle is twice the area of the quadrilateral if and only if a diagonal of the quadrilateral is parallel to two parallel sides of the rectangle.

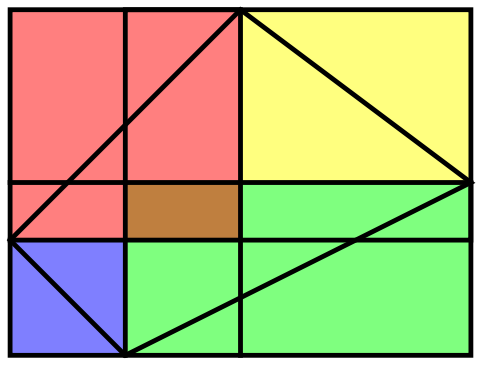
Now it is time for a solution where I use the sample rectangle pictured below. We draw lines parallel to the sides of the rectangle from every vertex of the quadrilateral. Now, we can find four pairs of congruent triangles where one triangle is inside the quadrilateral and the other is outside. In the picture below, the pairs are colored the same color. We see that green and red rectangles overlap, creating a brown rectangle. The fact that they overlap means that the quadrilateral’s area is less than half of the rectangle’s area.

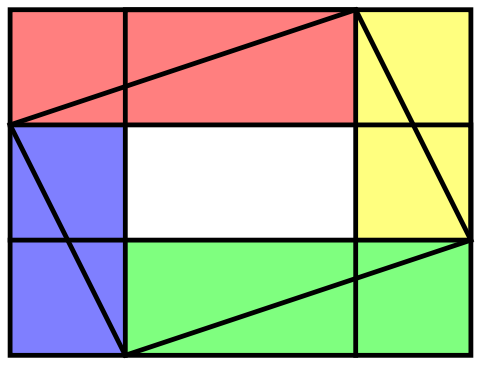
It could go the other way, as the next picture shows. Here, the quadrilateral’s area is more than half of the rectangle’s area. In this case, we have an “underlap” as opposed to an overlap.

Therefore, the quadrilateral’s area is exactly half of the rectangle’s if and only if there is no overlap/underlap, implying that the thickness of the overlap/underlap rectangle is zero. This means that one of the diagonals of the quadrilateral has to be parallel to two sides of the rectangle.