Tanya Khovanova's Math Blog

The 1978 Ukrainian Math Olympiad

6th April 2022, 02:48 pm

Ukraine is on my mind. Here is a problem for 9-graders from the 1978 Ukrainian Math Olympiad:

Problem. Prove that for every natural number n, the following number is not an integer.

Category: Math Competitions, Puzzles | Comment (RSS) | Trackback

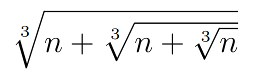
Anatoly:

I think perhaps the “trick” here is to see that cuberoot(n+cuberoot(n)) is already never an integer. If it were, n would be some x^3, and x^3+x would be a cube, but the smallest cube larger than x^3 is x^3+3x^2+3x+1.
7 April 2022, 3:57 am
Graham:

Isn’t this almost trivial?

For the result to be an integer, all the terms under the cube roots have to be integers (because all cubes of integers are integers) and so do all the cube roots.
In particular, the rightmost must be an integer. So n = a^3, for some a.

But if a is an integer, a^3 < a^3 + a < (a+1)^3, so the cube root of a^3 + a (which is the middle term) cannot be an integer.
7 April 2022, 6:52 am