Reversible Tetrahedra
Do you know what an isosceles tetrahedron is? I didn’t until recently. An isosceles tetrahedron has all of its faces congruent. Equivalently, all pairs of opposite edges are of equal length. Such tetrahedra are also called disphenoids. Here are some cute statements about them.
- If the four faces of a tetrahedron all have the same perimeter, then the tetrahedron is a disphenoid.
- If the four faces of a tetrahedron all have the same area, then the tetrahedron is a disphenoid.
Disphenoids have three nontrivial symmetries: 180-degree rotations around three lines connecting the midpoints of opposite edges.
Is it possible to have a tetrahedron with fewer symmetries than disphenoids? Yes, it is. Dan Klain just published a fascinating paper about such tetrahedra: Tetrahedra with Congruent Face Pairs. The results are so elegant and simple that I was surprised that they were new. I got curious and started to google aggressively. I found an official name for this kind of tetrahedron: phyllic disphenoid, but no theorems about them. Their name is quite unappealing: no wonder people didn’t want to study them much. Obviously, Dan wasn’t as aggressive at googling, so he didn’t find this official name and called them reversible tetrahedra. But my favorite name for them is the name Dan thought of but didn’t use in his paper: bi-isosceles tetrahedra.
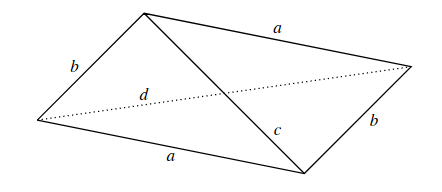
Here is the picture of a bi-isosceles tetrahedron from Dan’s paper. It has two faces with sides a, b, and c, and two faces with sides a, b, and d. The edges of this tetrahedron are: a, a, b, b, c, and d. It has one nontrivial symmetry: a 180-degree rotation around the line connecting the midpoints of the unequal opposite edges c and d. The picture emphasizes this symmetry. The figure in the picture is a projection of a bi-isosceles tetrahedron onto a plane, such that the line of symmetry is projected onto the point of symmetry of the projection. The two cute statements above, about disphenoids, can be generalized to the case of bi-isosceles tetrahedra.
- If the four faces of a tetrahedron can be split into two pairs with the same perimeter, then the tetrahedron is bi-isosceles.
- If the four faces of a tetrahedron can be split into two pairs with the same area, then the tetrahedron is bi-isosceles.
The first property is trivial, while the second one is proven in Dan’s paper. Dan also shows how to calculate the volume of a bi-isosceles tetrahedron:
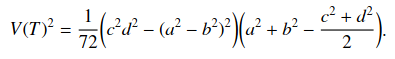
Share:
Igor:
Well, the volume of a tetrahedron is always a square root of a polynomial in squared edge-lengths. See for example this spelled out in Sabitov’s paper, equation (4):
https://iopscience.iop.org/article/10.1070/RM2011v066n03ABEH004748/pdf
11 March 2022, 5:47 pmThe reversible tetrahedron – The nth Root:
[…] If the four faces of a tetrahedron all have the same perimeter, then the tetrahedron is a disphenoid. If the four faces of a tetrahedron all have the same area, then the tetrahedron is a disphenoid. Disphenoids have three nontrivial symmetries: 180-degree rotations around three lines connecting the midpoints of opposite edges. … (Tanya Khovanova’s Math Blog) […]
13 March 2022, 8:01 pm