Tanya Khovanova's Math Blog

My son, Alexey Radul, wrote a program that finds the largest numbers to start a sequence in the Online Encyclopedia of Integer Sequences (OEIS). To my surprise, the top ten are all numbers consisting of ones only. The largest number is 11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111: a number with 128 ones. The sequence is A095646: a(n) is 128 written in base n. It starts with base 1, or more precisely, the unary expansion, which indeed requires 128 ones to express the number 128.

I decided to expand my top list to 50. Again, most of the numbers are bunches of ones: 48 out of the top 50 numbers are unary expansions of numbers 81 through 128. There are two more numbers in the top 50 that are different and belong to awesome sequences.

The first awesome sequence is sequence A033290: Ten consecutive primes in arithmetic progression. It starts with the number 100996972469714247637786655587969840329509324689190041803603417758904341703348882159067229719, which has 93 digits. This number takes 37th place on my list.

The second awesome sequence is sequence A291042: One powerful arithmetic progression with a nontrivial difference and maximal length. The sequence corresponds to a cool puzzle that appeared in the American Mathematical Monthly in 2000. The question was, “What is the length of the longest non-constant arithmetic progression of integers with the property that the kth term is a perfect kth power?” The answer is 5. John P. Robertson proved that such progression can’t have 6 terms and provided an example of a sequence with 5 terms, which is the sequence in the OEIS.

Here is how to construct this sequence. Start with an arithmetic progression 1, 9, 17, 25, 33, and multiply each term by 3²⁴5³⁰11²⁴17²⁰: the result is also an arithmetic progression. The first term is trivially a first power. The second term is 3²⁶5³⁰11²⁴17²⁰ = (3¹³5¹⁵11¹²17¹⁰)² and a square. The third term is 3²⁴5³⁰11²⁴17²¹ = (3⁸5¹⁰11⁸17⁷)³ and a cube. The fourth term is 3²⁴5³²11²⁴17²⁰ = (3⁶5⁸11⁶17⁵)³ and a fourth power. The fifth term is 3²⁵5³⁰11²⁵17²⁰ = (3⁵5⁶11⁵17⁴)⁵ and a fifth power.

The sequence starts with the number 10529630094750052867957659797284314695762718513641400204044879414141178131103515625. It has 83 digits, and it takes 48th place on my list.

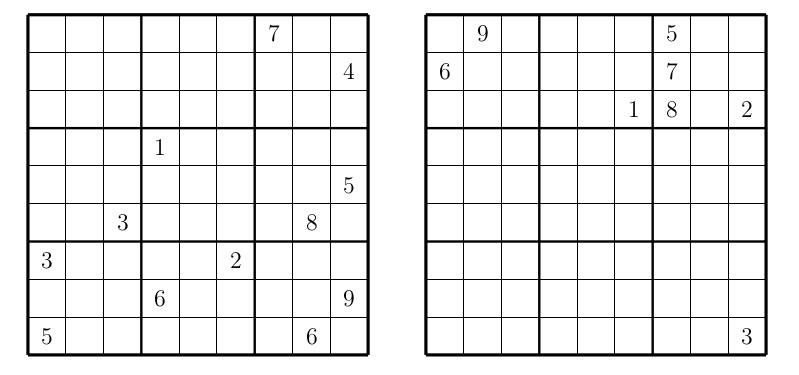
My students (Matvey Borodin, Eric Chen, Aidan Duncan, Boyan Litchev, Jiahe Liu, Veronika Moroz, Matthew Qian, Rohith Raghavan, Garima Rastogi, Michael Voigt) and I recently wrote a paper connecting the stable marriage problem and Sudoku. I just blogged about it. By the way, my students are in grades 7-9.

On the way, we invented a new type of Sudoku, which we call joint-groups Sudoku. This type is in contrast to a famous type of Sudoku, called disjoint-groups Sudoku. In a disjoint-groups Sudoku, in a particular place in a 3 by 3 box, all the digits are distinct across all the boxes. For example, the top-left corners of nine boxes have all the digits 1 thought 9. This creates nine additional disconnected regions (depending on the placements inside a 3 by 3 box) to add to columns, rows, and boxes that have to contain distinct digits.

For our new type, we wanted the digits in a particular place in each box, instead of being different, to be the same as much as possible. How much of sameness is possible? The first row contains three top-left corners. Thus, by Sudoku rules, these top-left corners have to be distinct. Thus, the top-left corners in all nine boxes have to contain at least three distinct digits. So here is the rule for the joint-groups Sudoku: the nine digits in a particular place in a 3 by 3 box contain not more than three distinct digits. It is easy to see that it means they contain exactly 3 distinct digits, each of them three times.

Here are two Sudoku puzzles from our paper. Each puzzle, when completed, forms a joint-groups Sudoku.

As you may know, I run PRIMES STEP, a local program where we do mathematical research with students in grades 6-9. Last academic year, we looked at the stable marriage problem and discovered its connection to Sudoku. Our paper The Stable Matching Problem and Sudoku (written jointly with Matvey Borodin, Eric Chen, Aidan Duncan, Boyan Litchev, Jiahe Liu, Veronika Moroz, Matthew Qian, Rohith Raghavan, Garima Rastogi, Michael Voigt) is now available at the arxiv.

Consider 3 men and 3 women who want to be married to each other in heterosexual couples. They rank each other without ties. The resulting 6 permutations of numbers 1, 2, and 3 that describe the six rankings are called the preference profile of this group of people. A matching is unstable if two people would be happier to run away together than to marry into the assigned couples. The two potential runaways are called a rogue couple. A matching is called stable if no rogue couple exists. The Gale-Shapley algorithm, invented by Gale and Shapley, finds a stable matching for any preference profile, implying that stable matching is always possible.

We discovered that preference profiles form a natural bijection with ways to place one digit into a Sudoku grid. So we wrote a paper describing the stable marriage, rogue couples, the Gale-Shapley algorithm, soulmates, and such in terms of Sudoku.

Oops, I forgot to explain who the soulmates are. We invented this term to describe two people who rank each other first. Though it is possible to have several stable matchings for the same preference profile if the soulmates exist, they must always be matched together.

We also invented a new Sudoku type, which I will explain next time.