SET Tic-Tac-Toe
The academic year is over and my junior PRIMES STEP group finished their paper about a classification of magic SET squares. A magic SET square is a 3 by 3 square of SET cards such that each row, column, and diagonal is a set. See an example below. The paper is posted at the arXiv:2006.04764.
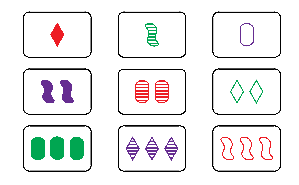
In addition to classifying the magic SET squares, my students invented the game of SET tic-tac-toe. It is played on nine cards that form a magic SET square. Two players take turns picking a card from the square. The first player who has a set wins.
One might think that this game is the same as tic-tac-toe, as a player wins as soon at they have cards from the same row, column, or diagonal. But if you build a magic SET square, you might notices that each magic SET square contains 12 sets. In addition to rows, columns, and diagonals, there are sets that form broken diagonals. The picture below shows all the sets in a magic SET square.
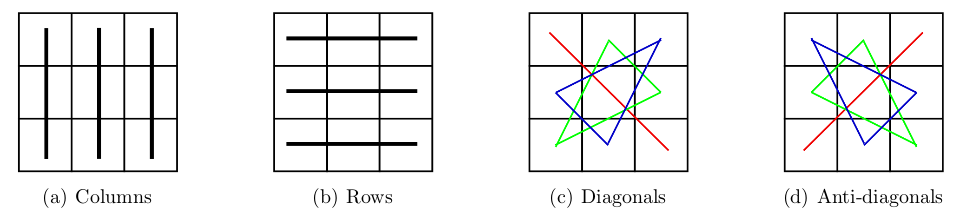
There are more ways to win in this game than in a regular tic-tac-toe game. My students proved that ties are impossible in this game. They also showed, that, if played correctly, the first player always wins.
Share:
Cristóbal Camarero:
SET tic-tac-toe is tic-tac-toe over a torus. We can see that 5 points/cards are enough to get a whole line by a counting argument. As 2 points define a line, if we were to get 5 points with only 2 points per line we would get at least 10 lines. There are 12 lines, but some are parallel, having 4 different directions. There are 3 lines in each direction. We could try to divide the expected 10 lines as 10=3+3+2+2 or 10=3+3+3+1, this is, a partition of the 10 lines with each summand representing the number of lines with 2 selected points for each of the four directions. However, if we have 2 points in all the lines of a given direction then we have at least 6 points.
26 June 2020, 1:51 pm