Tanya Khovanova's Math Blog

My STEP students invented a coin-flipping game that doesn’t require a coin. It is called The No-Flippancy Game.

Alice and Bob choose distinct strings of length n consisting of the letters H (for heads) and T (for tails). The two players alternate selecting the outcome of the next “flip” to add to the sequence by the rule below.

The “flip” rule: Let i < n be the maximal length of a suffix of the sequence of chosen outcomes that coincides with a prefix of the current player’s string. The player then selects the element of their string with index i + 1 as the next term in the sequence.

Alice goes first, and whoever’s string appears first in the sequence of choices wins. In layman terms, the game rules mean that the players are not strategizing, but rather greedily finishing their strings.

Suppose n = 2 and Alice chose HH. If Bob chooses HT, then Bob wins. Alice has to choose H for the first flip. Then Bob chooses T and wins. On the other hand, if Bob chooses TT for his string, the game becomes infinite. On her turn, Alice always chooses H, while on his turn Bob always chooses T. The game outcome is an alternating string HTHTHT… and no one wins.

Suppose n = 4, Alice chooses HHTT, and Bob chooses THHH. The game proceeds as HTHHTHHH, at which point Bob wins.

This game is very interesting. The outcome depends on how Alice’s and Bob’s chosen strings overlap with each other. We wrote a paper about this game, which is available at math.CO arXiv:2006.09588.

2020 MIT Mystery Hunt

Every year I write about latest MIT Mystery Hunt puzzles that might be appealing to mathematicians. Before diving into mathy puzzles, I would like to mention two special ones:

• Fortune Cookies—Our team laughed at this one.
• No Clue Crossword—Our team was puzzled by this one.

Unfortunately math wasn’t prominent this year:

• Food Court—This is a probability puzzle that is surprisingly uninspiring. There is no mystery: the puzzle page contains a list of probability problems of several famous types. But this puzzles can find great use in probability classes.
• Torsion Twirl—Mixture of dancing and equations. I love it.
• People Mover—Logical deduction at the first stage.

On the other hand, Nikoli-type puzzles were represented very well:

• The Ferris of Them All—Several different Nikoli puzzles on a wheel.
• Toddler Tilt—Not exactly a Nicoli puzzle, but some weird logic on a grid, some music too.
• The Dollhouse Tour—Not exactly a Nicoli puzzle, but some weird logic on a grid, some pictures too.
• The Nauseator—The first part of the puzzle is a huge nonogram.
• Domino Maze—A non-trivial Thinkfun puzzle.
• Backlot—Finding a path on a grid with a fractal structure.
• Whale—Variation on Rush Hour.

Some computer sciency puzzles:

• Hackin’ the Beanstalk—Hidden algorithms.
• Turtle—LogoWriter.
• Bear—Origami.

Cryptography:

• The Scottish Display—You are given trigrams.
• Pig—The pigpen cypher.
• ANDARAC—You are given gibberish looking telegrams.

A couple of puzzles with the mathy side hidden:

• Tunnel of Love.
• Pied Piper—A puzzle type that I like and promoted is hidden here.

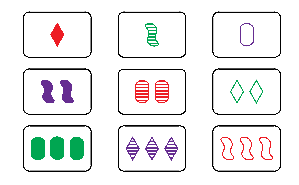
The academic year is over and my junior PRIMES STEP group finished their paper about a classification of magic SET squares. A magic SET square is a 3 by 3 square of SET cards such that each row, column, and diagonal is a set. See an example below. The paper is posted at the arXiv:2006.04764.

In addition to classifying the magic SET squares, my students invented the game of SET tic-tac-toe. It is played on nine cards that form a magic SET square. Two players take turns picking a card from the square. The first player who has a set wins.

One might think that this game is the same as tic-tac-toe, as a player wins as soon at they have cards from the same row, column, or diagonal. But if you build a magic SET square, you might notices that each magic SET square contains 12 sets. In addition to rows, columns, and diagonals, there are sets that form broken diagonals. The picture below shows all the sets in a magic SET square.

There are more ways to win in this game than in a regular tic-tac-toe game. My students proved that ties are impossible in this game. They also showed, that, if played correctly, the first player always wins.

You probably heard in the news that more men are dying from coronavirus than women. But not in Massachusetts. Here the proportion of women is about 52 percent. Why is this the case? Being a woman, should I be worried that I live in Massachusetts?

We know that coronavirus strikes older people harder than younger ones. Thus, we should take age into account. In the US more boys are born than girls. By the age of 40 the ratio evens out. Starting from 40 there are more women than men. With each next age group, the disparity increases. According to a recent US population report and for ages 85 and over there are about 4.22 million women versus 2.33 men: the proportion is almost 2 to 1.

As the coronavirus targets older people, were it gender-neutral, we would have had way more female deaths than male. This is not the case. So it hits males harder than females. But why are the ratios of female to male deaths different for different countries and states?

One simple explanation is that this is related to life expectancy and the age of the population. The older the population, the bigger the percentage of females. Which in turn increases the proportion of female deaths.

It could also be that Massachusetts has good health care making the average age of dying patients older than the average age for the country. This in turn will increase the proportion of females dying from coronavirus. No, I am not worried about living in Massachusetts.

I grew up in the USSR, where I was clueless about the race issues in the US. I have now lived in the US for 30 years, and still feel that there are many things about race that I do not understand. As a result, I am afraid to speak about it. I am worried that I’ll say something wrong. Recent events have encouraged me to say something. This is my first piece about race.

I came back to mathematics 10 year ago and started working at MIT. I love it. With some exceptions.

Many mathematicians are introverts or snobs or gender-biased. They are not usually friendly. I often walk down a corridor and people who are coming towards don’t notice me. If I say hello, they might not even reply or raise their eyes. It could be they are thinking about their next great theorem and do not notice me. It could be that I am not faculty and therefore do not deserve their attention. It could be that as a women I am not worth of their hello.

Soon after I started working at MIT, I was reminded of one of the reasons I left academia. It was this unfriendliness. But this time was different. First, I had grown a thicker skin. Second, I was working within a group. People who were working with me were nice to me. It was enough and so I stayed.

With time I adopted the same style: passing people without saying `Hello.’ Mostly I got tired of people not replying to my hello.

One day I was passing this man who, as had happened many times before, purposefully didn’t look at me. I thought my usual thought: another introverted/snobbish/gender-biased mathematician. Then I suddenly stopped in my tracks. My logic was wrong. This guy was Black. The unfriendliness of mathematicians is surely way worse for him than for me. It could be that he is looking at the floor for the same reason I do it: he is afraid that people will ignore his greeting. I failed to think about race deep enough before this realization. What happened next should have happened years earlier.

I took the initiative and the next couple of times I saw him, I said hello. This was all it took—two hellos—to change the whole feeling between us. The guy has a great smile.