Freedom and Diamonds
As you might have guessed from the title, this essay is about domino tilings.
Suppose a subset of a square grid has area N, and the number of possible domino tilings is T. Let’s imagine that each cell is contributing a factor of x tilings to the total independently of the others. Then we get that xN = T. This mental exercise suggests a definition: we call the nth root of T the degree of freedom per square for a given region.
Let’s consider a 1 by 2k rectangle. There is exactly one way to tile it with dominoes. So the degree of freedom per square of such a rectangle is 1. Now consider a 2 by k rectangle. It has the same area as before, and we know that there should be more than one tiling. Hence, we expect the degree of freedom to be larger than the one in the previous example. The number of tilings of a 2 by k rectangle is Fk-2, where Fk is kth Fibonacci number. So the degree of freedom for large k will be approximately the square root of the golden ratio, which is about 1.272.
You might expect that squares should give larger degrees of freedom than rectangles of the same area. The degree of freedom for a large square is about 1.3385. You can find more information in the beautiful paper Tilings by Federico Ardila and Richard P. Stanley.
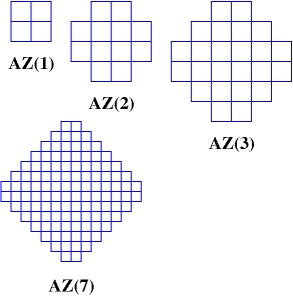
Let’s move from rectangles to Aztec diamonds. They are almost like squares but the side of the diamond is aligned with diagonals of the dominoes rather than with their sides. See the sample diamonds in the picture above, which Richard Stanley kindly sent to me for this essay.
It is easier to calculate the degree of freedom for Aztec diamonds than for regular squares. The degree is the fourth root of 2, or 1.1892…. In the picture below created by James Propp’s tiling group you can see a random tiling of a large Aztec diamond.
Look at its colors: horizontal dominoes are yellow and blue; vertical ones are red and aquamarine. You might wonder what rule decides which of the horizontal dominoes are yellow and which are blue. I will not tell you the rule; I will just hint that it is simple.

Back to freedom. As you can see from the picture, freedom is highly non-uniform and depends on where you live. Freedom is concentrated inside a circle called the arctic circle, perhaps because the areas outside it are frozen for lack of freedom.
Now I would like to expand the notion of freedom to give each cell its own freedom. For a large Aztec diamond, I will approximate freedom with a function that is one outside the arctic circle and is uniform inside. The Aztec diamond AZ(n) consists of 2n(n+1) squares, shaped like a square with side-length n√2. So the area of the circle is πn2/2. Hence we can calculate the freedom inside the circle as the πth root of 2, which is about 1.247. This number is still much less than the degree of freedom of a cell in a large square.
Share:
Jim Propp:
Thanks for writing this!
Moving beyond your approximation of local freedom (1 outside the arctic circle and constant inside) there’s a more precise way to define local freedom: it starts at 1 on the arctic circle and steadily increases as one moves inward, achieving maximal freedom (the same degree of freedom large squares have) in the center. Maximal freedom is achieved only in the middle. When n is large enough, a patch of the Aztec diamond of order n that’s even 1% (i.e., distance n/100) away from the center has small but measurable deviations from maximal freedom. And more is true: For large n, the relative proportions of red, blue, yellow, and green in a patch allow you to figure out what part of the Aztec diamond the patch came from (its “latitude and longitude”, in a manner of speaking), with probability exponentially close to 1.
Putting this more colorfully: If you parachuted down into an Aztec diamond tiling of order one million, with its tiles colored, you could figure out your relative position within the Aztec diamond fairly accurately by looking at the nearby tiles and taking a census of their colors — UNLESS you were unlucky enough to land outside the arctic circle. Then all you’d see are tiles of a single color, and all you’d know is which of the four frozen regions you were in.
27 May 2011, 10:24 amTanya Khovanova:
Jim,
This is so cool!
27 May 2011, 10:39 amMarcial Fonseca:
Hi Tanya, I enjoy very much your excellent and beautiful page. I have sent you 3 emails from two different addresses to your Gmail but apparently you have no received them or you are no reading your email. Two of the emails are 2 questions and the other is a joke for you humour section.
30 May 2011, 1:12 amBest regards, MF
Marcial Fonseca:
Tanya, sorry for the lapsus calami. Actualy I sent the emails to your yahoo accouunt. Regards….MF
30 May 2011, 2:56 amSeventh Linkfest:
[…] Tanya Khovanova: Freedom and Diamonds […]
11 June 2011, 2:58 pmJoe DeVincentis:
The rule that determines the yellow or blue color is parity-based. Suppose you colored the unit squares in a checkerboard fashion. Then the horizontal dominoes whose left square is black are colored one color, and those whose left square is white are the other color.
Now if, on the other hand, you were to cut one of these Aztec diamonds in half along one of its orthogonal axes, there is only one way to tile it.
2 June 2012, 12:12 pm